高中数学人教版第一册上册函数同步练习题

这是一份高中数学人教版第一册上册函数同步练习题，共18页。

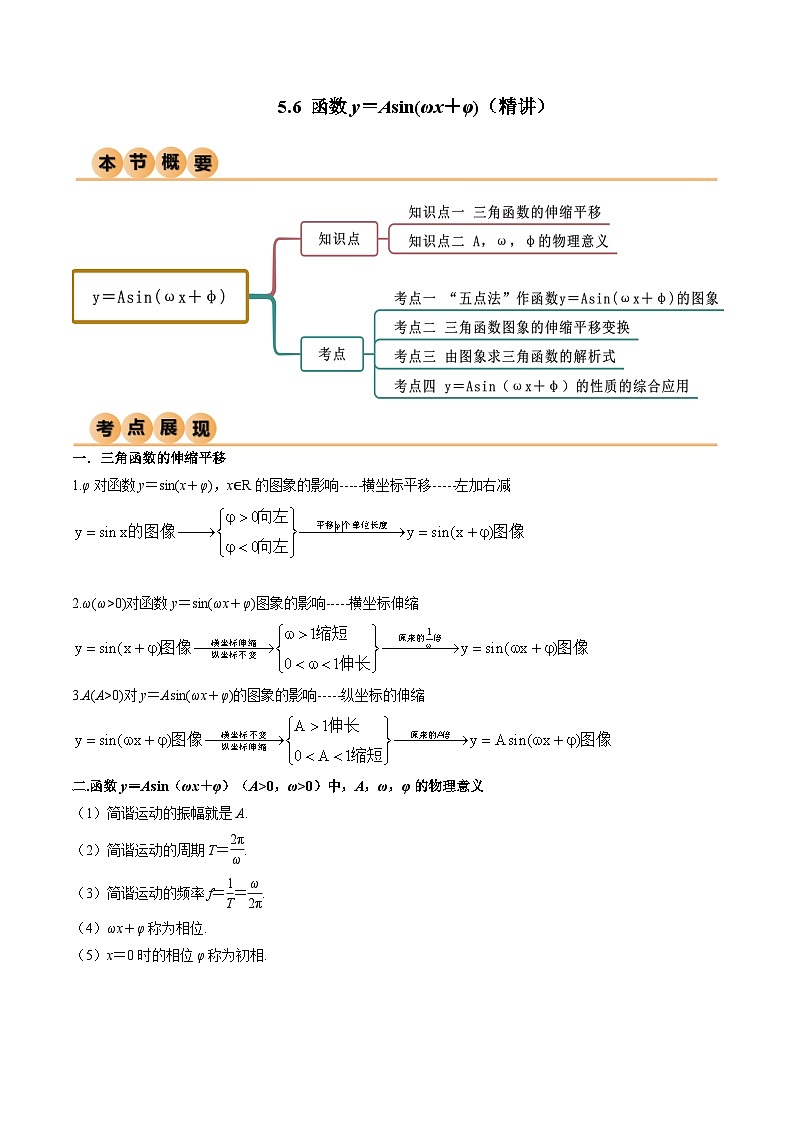
一．三角函数的伸缩平移
1.φ对函数y＝sin(x＋φ)，x∈R的图象的影响-----横坐标平移-----左加右减
2.ω(ω>0)对函数y＝sin(ωx＋φ)图象的影响-----横坐标伸缩
3.A(A>0)对y＝Asin(ωx＋φ)的图象的影响-----纵坐标的伸缩
二.函数y＝Asin（ωx＋φ）（A>0，ω>0）中，A，ω，φ的物理意义
（1）简谐运动的振幅就是A.
（2）简谐运动的周期T＝eq \f(2π,ω).
（3）简谐运动的频率f＝eq \f(1,T)＝eq \f(ω,2π).
（4）ωx＋φ称为相位.
（5）x＝0时的相位φ称为初相.
一．图象平移变换的方法
(1)确定平移方向和平移的量是解决平移变换的关键．
(2)当x的系数是1时，若φ>0，则左移φ个单位；若φ<0，则右移|φ|个单位．
(3)当x的系数是ω(ω>0)时，若φ>0，则左移eq \f(φ,ω)个单位；若φ<0，则右移eq \f(|φ|,ω)个单位．
二．“五点法”作图
1.实质：利用“五点法”作函数f(x)＝Asin(ωx＋φ)的图象，实质是利用函数的三个零点，两个最值点画出函数在一个周期内的图象．
2．用“五点法”作函数f(x)＝Asin(ωx＋φ)的图象的步骤
第一步：列表
第二步：在同一坐标系中描出各点．
第三步：用光滑曲线连接这些点，形成图象．
三．由y＝Asin(ωx＋φ)的图象求其解析式的常用方法
方法一：最值法
(1)A：一般可由图象的最高点和最低点的纵坐标来确定|A|，|A|＝eq \f(fxmax－fxmin,2).
(2)ω：因为T＝eq \f(2π,ω)，所以往往通过求周期T来确定ω.可通过已知曲线及其与x轴的交点来确定T，注意相邻的最高点与最低点之间的水平距离为eq \f(T,2)，相邻的两个最高点(最低点)之间的水平距离为T.
(3)φ：以五点作图法中的最高点作为突破口，即当ωx＋φ＝eq \f(π,2)＋2kπ，k∈Z时，y有最大值，或者由五点作图法中的第一个点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(φ,ω)，0))作为突破口，从图象的升降情况找准第一点的位置．
方法二：“五点”对应法
依据五点作图法的原理，点的序号与式子的关系如下；
“第一点”(即图象第一次上升时与x轴的交点)横坐标满足ωx＋φ＝0；
“第二点”(即图象的“峰点”)横坐标满足ωx＋φ＝eq \f(π,2)；
“第三点”(即图象下降时与x轴的交点)横坐标满足ωx＋φ＝π；
“第四点”(即图象的“谷点”)横坐标满足ωx＋φ＝eq \f(3π,2)；
“第五点”(即图象第二次上升时与x轴的交点)横坐标满足ωx＋φ＝2π.
考点一 “五点法”作函数y＝Asin(ωx＋φ)的图象
【例1】（2023春·云南昆明·高一校考阶段练习）（1）利用“五点法”画出函数在长度为一个周期的闭区间的简图.
列表:
作图:

（2）并说明该函数图象可由的图象经过怎么变换得到的.
【答案】（1）答案见解析；（2）答案见解析.
【解析】（1）先列表，后描点并画图.
（2）把的图象上所有的点向左平移个单位，得到的图象，再把所得图象的点的横坐标伸长到原来的2倍（纵坐标不变），得到的图象.
【一隅三反】
1．（2023春·江西南昌·高一校考阶段练习）已知函数
(1)用“五点法”画出函数在一个周期内的图象；
(2)直接写出函数的值域和最小正周期．
列表：
作图：

【答案】(1)答案见解析
(2)值域，最小正周期为
【解析】（1）解：列表:
图象如图所示：

（2）解：因为，则，
故函数的值域为，最小正周期为.
2．（2023春·北京·高一校考开学考试）已知函数.
(1)试用“五点法”画出它的图象；
列表：
作图：
(2)从正弦曲线出发，如何通过图象变换得到函数的图象？（两种方法）
【答案】(1)详见解析；
(2)详见解析；
【解析】（1）令，则，列表如下，
描点画图.
（2）方法一：先将的图象向左平移个单位，得到函数的图象，然后使曲线上各点的横坐标变为原来的2倍，得到函数的图象，最后将曲线上各点的纵坐标变为原来的，得到的图象.
方法二：先将的图象各点的横坐标变为原来的2倍，得到函数的图象，然后将曲线向左平移个单位，得到函数的图象，最后将曲线上各点的纵坐标变为原来的，得到的图象.
3．（2023·江西赣州·高一统考期末）设函数.
（1）在给定的平面直角坐标系中，用“五点法”画出函数在区间上的简图(请先列表，再描点连线)；
（2）若，求的值.
【答案】（1）答案见解析；（2）.
【解析】（1）列表如下：
（2）解：由，得，
由，
得，
由，
得，
则.
考点二 三角函数图象的伸缩平移变换
【例2-1】（2023秋·湖北武汉）要得到函数的图象，可以将函数的图象（ ）
A．向左平移个单位B．向左平移个单位
C．向右平移个单位D．向右平移个单位
【答案】B
【解析】因为,
所以将函数的图象向左平移个单位可得到函数的图象.
故选:B.
【例2-2】（2023秋·新疆·高一校联考期末）为了得到函数的图象，只要将函数图象上所有点的（ ）
A．横坐标缩短到原来的，纵坐标不变，再把得到的图象向右平移个单位长度
B．横坐标缩短到原来的，纵坐标不变，再把得到的图象向左平移个单位长度
C．横坐标缩短到原来的，纵坐标不变，再把得到的图象向右平移个单位长度
D．横坐标伸长到原来的2倍，纵坐标不变，再把得到的图象向右平移个单位长度
【答案】A
【解析】将图象上所有点的横坐标缩短到原来的，纵坐标不变，得，
再把得到的图象向右平移个单位长度，得到函数的图象．
故选：A
【例2-3】（2023·全国·高三专题练习）将函数的图像向左平移个单位长度后，得到的函数图像关于y轴对称，则的最小值为 .
【答案】
【解析】将函数的图像向左平移个单位长度后，
得到函数的图像，
因为图像关于轴对称，所以，，则，.
令，得的最小值为.
故答案为：
【例2-4】（2023春·上海嘉定·高一校考期中）把函数的图像适当变动就可以得到图像，这种变动可以是（ ）
A．向右平移B．向左平移C．向右平移D．向左平移
【答案】D
【解析】，，
函数的图象向左平移可以得到的图象.
故选：D
【一隅三反】
1．（2023秋·广西贵港）要得到函数的图象，需将函数的图象（ ）
A．向左平移个单位长度B．向右平移个单位长度
C．向左平移1个单位长度D．向右平移1个单位长度
【答案】B
【解析】由于，
所以将函数的图象向右平移个单位长度得到的图象．
故选：B
2．（2023春·四川绵阳·高一绵阳南山中学实验学校校考期中）为了得到函数的图象，只需要把函数图象（ ）
A．先将横坐标缩短到原来的倍（纵坐标不变），再向右平移个单位
B．先将横坐标缩短到原来的倍（纵坐标不变），再向右平移个单位
C．先向左平移个单位，再将横坐标伸长到原来的倍（纵坐标不变）
D．先向左平移个单位，再将横坐标伸长到原来的倍（纵坐标不变）
【答案】B
【解析】先将函数图像横坐标缩短到原来的倍（纵坐标不变）得到，
再向右平移个单位得到的图像；
或者将函数图像向右平移个单位，再将横坐标缩短到原来的倍（纵坐标不变）可得到的图像.
故选：B
3．（2023秋·河南焦作 ）已知函数，若将的图象向左平移个单位长度后所得的图象关于坐标原点对称，则m的最小值为（ ）
A．B．C．D．
【答案】B
【解析】的图象向左平移m个单位长度后，得到的图象对应函数，
因为的图象关于坐标原点对称，
所以，即，
因为，故当时，m取得最小值．
故选：B.
4．（2023春·广东广州）要得到函数的图像，只需把函数的图像（ ）
A．向左平移个单位长度B．向右平移个单位长度
C．向左平移个单位长度D．向右平移个单位长度
【答案】D
【解析】因为，
即只需要把函数的图像向右平移个单位长度即可.
故选：D
考点三 由图象求三角函数的解析式
【例3】（2023春·四川宜宾·高一校考阶段练习）（多选）已知函数（，，）的部分图象如图所示，则（ ）

A．的最小正周期为
B．当时，的值域为
C．为是偶函数
D．将的图象所有点的横坐标伸长到原来的2倍，纵坐标不变，得到的函数图象关于点对称
【答案】ACD
【解析】由图可知，，最小正周期，故选项A正确；
由，知，
因为，所以，
所以，，即，，
又，所以，
所以，
对于选项B，当时，，
所以，故选项B错误；
对于选项C，令，定义域为，
，所以为偶函数，即为偶函数，故选项C正确；
对于选项D，将函数的图象上所有点的横坐标伸长为原来的2倍，纵坐标不变，得到的图象，
因为当时，，故选项D正确.
故选：ACD.
【一隅三反】
1．（2023春·新疆伊犁·高一校联考期末）（多选）函数的部分图象如图所示，下列结论中正确的是（ ）

A．的最小正周期为
B．直线是函数图象的一条对称轴
C．函数的单调递增区间为
D．将函数的图象向右平移个单位得到函数的图象
【答案】CD
【解析】由图象可得，，，又，故，
所以.
显然A错误；
对于B项，，不是对称轴，故B错误；
对于C项，令，故C正确；
对于D项，将函数的图象向右平移个单位得，故D正确.
故选：CD.
2．（2023秋·四川成都 ）已知函数的部分图象如图所示，若将函数的图象向右平移个单位，得到函数的图象，则（ ）

A．B．
C．D．
【答案】C
【解析】由图象可知，，解得；
由振幅可知；
将代入可得，又，即可得，
因此，
易知，
故选：C.
3．（2023春·内蒙古呼和浩特·高一呼市二中校考期末）已知函数的部分图象如图所示，为了得到函数的图象，只要把的图象上所有的点（ ）

A．向左平行移动个单位长度B．向右平行移动个单位长度
C．向左平行移动个单位长度D．向右平行移动个单位长度
【答案】D
【解析】根据题中函数的部分图象，结合五点法作图可得，
故，又，故，所以，
为了得到函数的图象，只要把的图象上所有的点向右平行移动个单位长度即可．
故选：D．
考点四 y＝Asin（ωx＋φ）的性质的综合应用
【例4】（2023春·江西赣州·高一统考期末）已如函数．
(1)用“五点法”作出函数在区间上的图像；
(2)将函数的图像向右平移个单位长度，再将图像上的每个点的横坐标都伸长为原来的2倍，纵坐标不变，得到函数的图像，求在区间上的取值范围．
【答案】(1)图像见解析
(2)
【解析】（1）依题意，列表如下：
所以数在区间上的图象如下：
.
（2）因为，
所以将函数的图像向右平移个单位长度，可得到的图像，
再将得到的图像上的每个点的横坐标都伸长为原来的2倍，纵坐标不变，可得到的图像，
因为，所以，则
故的取值范围是.
【一隅三反】
1．（2022·全国·高一专题练习）已知函数．
(1)若，求的值；
(2)将函数的图象向左平移个单位，得到函数的图象，求函数在上的值域．
【答案】(1)
(2)
【解析】（1），
由，得，即，
故或，，
即或，，又∵∴；
（2）将函数的图象向左平移个单位，可得函数图象的解析式为，，
，
所以函数在上的值域为．
2．（2023春·江西·高一校联考期末）已知函数.
(1)求的最大值及相应的取值；
(2)若把的图象向左平移个单位长度得到的图象，求在上的单调递增区间.
【答案】(1)时，取得最大值.
(2).
【解析】（1）因为
所以当，
即时，取得最大值.
（2），
由，
得:，
取得：在上的单调递增区间为
3．（2023春·广东江门·高一鹤山市第一中学校考阶段练习）已知函数.
(1)求函数的最小正周期；
(2)将函数的图象向下平移个单位长度，再把横坐标缩短到原来的倍（纵坐标不变），得到函数的图象，当时，若方程有两个不等的实根，求实数的取值范围.
【答案】(1)；
(2).
【解析】（1）
,
故函数的最小正周期为.
（2）将函数的图象向下平移个单位长度，得到的图象，
再把横坐标缩短到原来的倍（纵坐标不变），得到的图象.
当时，，令,
当时,方程有两个不等的实根，
即与的图象在上有两个交点,
画出在上的图象如图所示：
由图可得，
故实数的取值范围为.
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
－eq \f(φ,ω)
eq \f(π,2ω)－eq \f(φ,ω)
eq \f(π,ω)－eq \f(φ,ω)
eq \f(3π,2ω)－eq \f(φ,ω)
eq \f(2π,ω)－eq \f(φ,ω)
f(x)
0
A
0
－A
0
x
y
0
x
y
0
1
0
0
0

0
2
0
-2
0
2