云南省曲靖市2023-2024学年七年级上学期期末数学试题

这是一份云南省曲靖市2023-2024学年七年级上学期期末数学试题，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列方程中，是一元一次方程的是（ ）
A．3x-y=6B．x2+x-3=0 C．4x=12D．4x-1=24
【答案】C
【解析】A．3x-y=6中有两个未知数，故本选项不符合题意；
B．x2+x-3=0，未知数得最高次是2次，不是一元一次方程，不符合题意；
C．4x=12，是一元一次方程，故本选项符合题意；
D．4x-1=24，不是整式方程，不是一元一次方程，故本选项不符合题意．
故选：C．
2．七年级（1）班期末考试数学的平均成绩是83分，小亮得了90分，记作+7分，小英的成绩记作-3分，表示得了（ ）
A．86分B．93分C．87分D．80分
【答案】D
【解析】∵年级（1）班期末考试数学的平均成绩是83分，小亮得了90分，记作+7分，
∴小英的成绩记作-3分，表示得了83+-3=80分，
故选D．
3．在数轴上，把表示-3的点A沿着数轴向正方向移动6个单位长度，到达点B，则点B表示的数是（ ）
A．3B．-9C．9D．-3
【答案】A
【解析】由题意得：
点B表示的数为-3+6=3，
故选：A．
4．如图，已知O是直线AB上一点，∠1=130°，OD平分∠BOC，则∠BOD的度数是（ ）
A．25°B．26°C．27°D．28°
【答案】A
【解析】∵∠1=130°，
∴∠COB=180°-130°=50°，
∵OD平分∠BOC，∴∠2=12∠BOC=12∠COB=25°．故选：A．
5．下列说法中正确的是（ ）
A．0是最小的正整数
B．多项式-x2y+52xy-7是三次三项式
C．1.30×104精确到百分位
D．单项式13πx2的系数是13
【答案】B
【解析】A、1是最小的正整数；不符合题意，
B、多项式-x2y+52xy-7是三次三项式，故B符合题意；
C、1.30×104精确到百位，故C不符合题意；
D、单项式13πx2的系数是13π，故D不符合题意；故选：B．
6．如图，已知线段a，b．按如下步骤完成尺规作图：①作射线AM；③在线段AB上截取AD=BD=a ，BC=b．则AC的长是（ ）
A．2a+b B． a+b C．2a-b D． b-a
【答案】C
【解析】如图，AC=AB-BC=AD+BD-BC=2a-b．
故选：C．
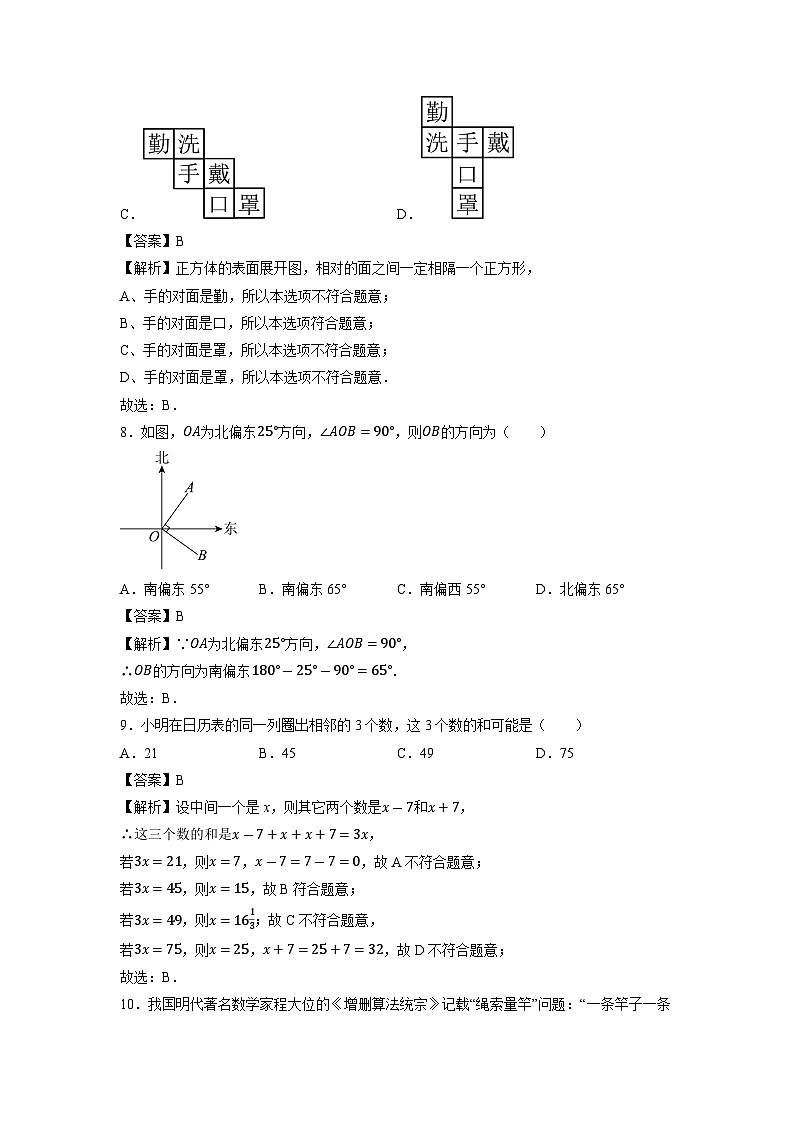
7．下列正方体的展开图上每个面上都有一个汉字．其中，手的对面是口的是（ ）
A． B．
C． D．
【答案】B
【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，
A、手的对面是勤，所以本选项不符合题意；
B、手的对面是口，所以本选项符合题意；
C、手的对面是罩，所以本选项不符合题意；
D、手的对面是罩，所以本选项不符合题意．
故选：B．
8．如图，OA为北偏东25°方向，∠AOB=90°，则OB的方向为（ ）

A．南偏东55°B．南偏东65°C．南偏西55°D．北偏东65°
【答案】B
【解析】∵OA为北偏东25°方向，∠AOB=90°，
∴OB的方向为南偏东180°-25°-90°=65°．
故选：B．
9．小明在日历表的同一列圈出相邻的3个数，这3个数的和可能是（ ）
A．21B．45C．49D．75
【答案】B
【解析】设中间一个是x，则其它两个数是x-7和x+7，
∴这三个数的和是x-7+x+x+7=3x，
若3x=21，则x=7，x-7=7-7=0，故A不符合题意；
若3x=45，则x=15，故B符合题意；
若3x=49，则x=1613；故C不符合题意，
若3x=75，则x=25，x+7=25+7=32，故D不符合题意；
故选：B．
10．我国明代著名数学家程大位的《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托，折回索子却量竿，用绳索去量竿，绳索比竿长5尺，就比竿短5尺．设竿长为x尺，根据题意列一元一次方程（ ）
A．12x+5=x-5B．12x-5=x+5
C．12x+5=x-5D．12x-5=x+5
【答案】C
【解析】设杆子为x尺，则索为x+5尺，根据“折回索子却量竿，却比竿子短一托”，即可得出关于x一元一次方程．
【解答】解：设杆子为x托，则索为x+5尺，
根据题意得：12x+5=x-5，
故选：C．
11．生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，我们就用数学模型2n来表示．即：21=2，22=4，23=8，24=16，25=32，…，请你推算22024的个位数字是（ ）
A．6B．4C．2D．8
【答案】A
【解析】由题意知，2n个位数字每四个数按2，4，8，6循环出现，
∵2024÷4=506，
∴22024的个位数字与24相同，为6，
故选：A．
12．由于换季，商场准备对某商品打折出售，如果按原售价的七折出售，将亏损20元，而按原售价的八五折出售，将盈利10元，则该商品的原售价为（ ）
A．140元B．160元C．180元D．200元
【答案】D
【解析】设该商品的原售价为x元，
根据题意得：70%x+20=85%x-10，
解得：x=200，
则该商品的原售价为200元．
故选：D．
二、填空题
13．神舟十三号创造了中国航天员连续在轨飞行时间的最长纪录，该乘组共在轨飞行的1580000秒，这个飞行时间用科学记数法表示应为 秒．
【答案】1.58×106
【解析】1580000=1.58×106．
14．若|a-3|+(b+1)2=0，则ba= ．
【答案】-1
【解析】∵|a-3|+(b+1)2=0，
而(b+1)2≥0，|a-3|≥0．
∴a-3=0，b+1=0,
∴a=3，b=-1,
ba=（-1）3=-1.
15．若一个角的余角是38°，则这个角的补角为 ．
【答案】128°
【解析】∵一个角的余角为38°，
∴这个角为90°-38°=52°，
∴这个角的补角为180°-52°=128°.
16．当x=2时，代数式ax3+bx+4的值为7，则当x=-2时，代数式ax3+bx-7的值为 ．
【答案】-10
【解析】∵当x=2时，ax3+bx+4=7，
∴8a+2b=3，
当x=-2时，
ax3+bx-7
=-8a-2b-7
=-8a+2b-7
=-3-7
=-10.
三、解答题
17．计算：
(1)13+56-38×-24；
(2)-12+-0.5+1÷15×2--22．
解：（1）13+56-38×-24
=13×-24+56×-24-38×-24
=-8-20+9
=-19；
（2）-12+-0.5+1÷15×2--22
=-1+12÷15×2-4
=-1+12×5×-2
=-1-5
=-6.
18．解方程：
(1)4x-220-x=2；
(2)4x-14=2x+33-2．
解：（1）去括号，得4x-40+2x=2，
移项，得6x=42，
系数化为1，得x=7；
（2）去分母，得34x-1=42x+3-24，
去括号，得12x-3=8x+12-24，
移项合并同类项，得4x=-9，
系数化为1，得x=-94．
19．先化简，再求值：9a2b-2ab2-3ab2-3a2b，其中a=1，b=-12．
解：9a2b-2ab2-3ab2-3a2b
=9a2b-2ab2-3ab2+9a2b
=9a2b-2ab2+3ab2-9a2b
=ab2．
当a=1，b=-12时,原式=1×-122=14．
20．常态化疫情防控下，公众做好个人防护很重要．乘坐电梯、公共交通工具，进入人员密集的公共场所时，都应佩戴口罩．这使得近期医用口罩的需求大幅增加．某口罩加工厂为满足市场需求，计划在本周每日生产6000个医用口罩，但是由于各种原因，实际每日生产量与计划生产量相比情况如下表所示（增加的口罩数为正数，减少的口罩数为负数）：
(1)该口罩加工厂本周产量最多的一日比产量最少的一日多生产多少个口罩？
(2)该加工厂实行计件工资，每生产一个医用口罩，工资为0.3元，则该口罩加工厂本周应支付的工资总额是多少元？
解：（1）+450--200=650（个），
∴本周产量最多的一日比产量最少的一日多生产650个口罩；
（2）+150-200+100+350-50+450+150+6000×7=42950（个），
42950×0.3=12885（元），
答：该口罩加工厂本周应支付的工资总额是12885元．
21．甲地到乙地的高铁开通后，运行时间由原来的4小时缩短至1小时，运行里程缩短了20千米．已知高铁的平均速度比普通列车的平均速度每小时快220千米，求高铁的平均速度．
解：高铁的平均速度为x km/h，根据题意得，
4x-220-x=20，
解得x=300，
答：高铁的平均速度300千米每小时．
22．如图，C，D，E将线段AB分成2：4：4：6四部分，M，P，Q，N分别是AC，DE，EB的中点，求线段PQ的长度．
解：设AC=2x，CD=DE=4x，
∵M、N分别是AC，
∴MC=22AC=x13EB=3x，
∴x+4x+4x+6x=24，
解得x=2，
∴CD=DE=4x=8，
∵P，Q，N分别是CD，DE，EB的中点，
∴DP=13CD=4，DQ=18DE=4，
∴PQ=DP+DQ=4+6=8．
23．下表是某市居民每月用水收费标准（单位：元/立方米），设用户用水量为x立方米．
(1)据了解用水10立方米，需交水费35元，某用户10月份恰好用水30立方米，求该用户10月份应交水费多少元？
(2)该用户11月份交水费152元，求该用户11月份用水多少立方米？
解：（1）根据题意得：10a=35，
解得：a=3.5，
∴30a=30×3.5=105（元）．
答：该用户10月份应交水费105元；
（2）设该用户11月份用水x立方米，
∵105<152，
∴x>30．
根据题意得：105+3.5+1.2x-30=152，
解得：x=40．
答：该用户11月份用水40立方米．
24．如图1，在桌上放置一副三角板（忽略厚度），有两个角的顶点重合于一点O，∠COD=60°．

(1)如图2，绕着点O转动三角板COD（两个三角板有重叠），∠AOD+∠BOC的大小是否发生变化？若不发生变化，求出它的值；若发生变化，说明理由．
(2)在转动三角板COD的过程中（两个三角板有重叠），若∠AOC=4∠BOD，求∠BOD的度数．
解：（1）∵∠AOD+∠BOC=∠AOB+∠BOD+∠BOC，
=∠AOB+∠DOC
=90°+60°
=150°,
∴∠AOD+∠BOC的大小不变，∠AOD+∠BOC=150°，
（2）设∠BOD=x，则∠AOC=4x，
①当OD在∠AOB外时，
∴60-x=90-4x，
解得x=10，
∴∠BOD=10°，
②当OD在∠AOB内时，如图，

∴60+x=90-4x，
解得x=6，
∴∠BOD=6°,
∴∠BOD=10°或∠BOD=6°．星期
一
二
三
四
五
六
日
增减（单位：个）
＋150
-200
＋100
＋350
-50
＋450
＋150
用水量x（单位：立方米）
单价（单位：元/立方米）
x≤30
a
超出30的部分
a+1.2