第4章 基本平面图形-小结与复习 北师版七年级数学上册课件

这是一份第4章 基本平面图形-小结与复习 北师版七年级数学上册课件，共31页。

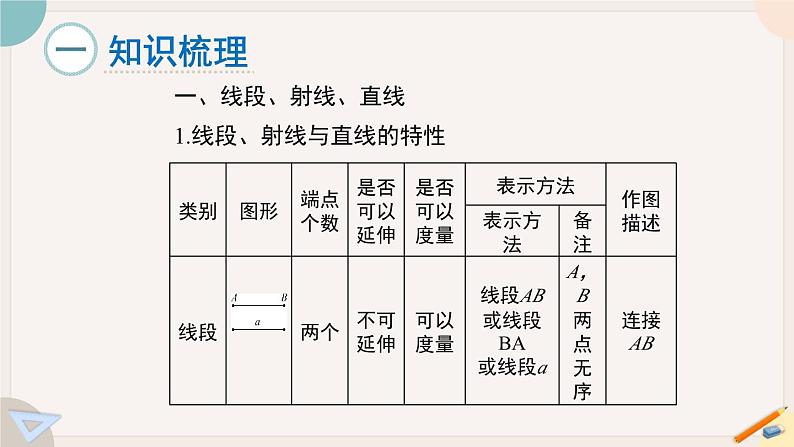
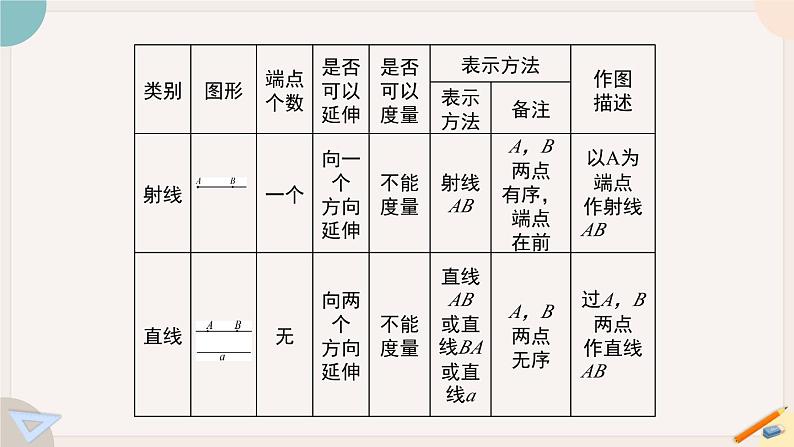
一、线段、射线、直线1.线段、射线与直线的特性2.两点确定一条直线经过两点有且只有一条直线．二、比较线段的长度1.线段的性质两点之间的所有连线中，线段________ ．简述为：两点之间，线段________ ．最短最短两点之间的距离是指连接两点的线段的________ ．长度2.两点之间的距离3.比较两条线段的长短(1)直接观察法；(2)度量法；(3)叠合法．4.线段的中点点M将线段AB分成_______的两条线段AM与BM，点M叫做线段AB的中点.相等三、角1.角的定义(1)角是由两条具有公共端点的射线组成的图形．(2)角可以看做是一条射线绕着它的端点旋转而成．2.角的表示方法3.平角与周角的概念一条射线绕它的端点旋转，当终边和始边成一条直线时，所成的角叫做________；终边继续旋转，当它又和始边________时，所成的角叫做周角．平角为180°，周角为360°.重合平角4.角的度量(1)角的度量单位是度、分、秒．(2)它们之间的关系是六十进制的，即1°＝60′，1′＝60″.5.方向角借助角表示方向，通常以正北或正南为基准，配以偏西或偏东的角度来描述方向．1.角的比较方法(1)直接观察法；(2)度量法；(3)叠合法．四、角的比较2.角的平分线从一个角的顶点引出的一条射线，把这个角分成__________的角，这条射线叫做这个角的平分线．两个相等五、多边形和圆的初步认识1.多边形(1)多边形是由若干条不在同一直线上的________首尾顺次相连组成的封闭____________ ．(2)连接多边形不相邻的两个顶点的线段叫做多边形的________ ．对角线线段平面图形2.正多边形各边相等，各角也相等的多边形叫做正多边形．3.圆的有关概念(1)在平面上，一条线段绕着它固定的一个端点旋转一周，另一个端点形成的图形叫做_______ .固定的端点称为________ ，这条线段称为_______．(2)圆上任意两点间的部分叫做圆弧，简称弧．(3)由一条弧和经过这条弧上的端点的两条半径所组成的图形叫做________ ．(4)顶点在圆心的角叫做________ ．圆心角圆圆心半径扇形 例1 如图，A，B，C，D为平面内每三点都不在一条直线上的四点，那么过其中任意的两点，可画出几条直线？若A，B，C，D，E为平面内每三点都不在一条直线上的五点，则过其中任意的两点可画几条直线？若是n个点呢？ 我们在探索物体的个数时，可首先求出各图中物体的个数，将其与相应的图序数作对比，看二者有何关系，即得规律． 【归纳总结】 例2 如图，线段AB＝32cm，点C在AB上，且AC∶CB＝5∶3，点D是AC的中点，点O是AB的中点，求DB与OC的长． 在求线段长时，我们常常结合图形转化为求相关线段的和或差，再结合线段中点的定义等进而求解(化未知为已知)． 【归纳总结】 例3 钟表在3点半时，它的时针和分针所成的锐角是(　　) A．70° B．75° C．85° D．90°B 例4 如图，∠AOB＝∠COD＝90° ，∠BOC＝42° ，则∠AOD＝(　　)A．48° B．148°C．138° D．128° 【解析】由图可知∠AOB、∠BOC、∠COD、∠AOD组成一个周角，所以∠AOD=360°－∠AOB－∠COD－∠BOC=138°.故选C.C 例5 (1)如图，已知∠AOB＝90°，∠BOC＝30°，OM平分∠AOC，ON平分∠BOC，求∠MON的度数；又因为∠AOB＝90°，所以∠MON＝45°. (2)如果(1)中∠AOB＝α，其他条件不变，求∠MON的度数； (3)如果(1)中∠BOC＝β(β为锐角)，其他条件不变，求∠MON的度数； 因为∠AOB＝90° 所以∠MON=45° (4)从(1)，(2)，(3)的结果中能看出什么规律？ 解： 分析(1)，(2)，(3)的结果和(1)的解答过程可知： ∠MON的大小总等于∠AOB的一半，而与锐角∠BOC的大小无关．6 3.钟表显示12点30分时，时针与分针的夹角为______．　165° 4．下午2时15分到5时30分，时钟的时针转过的度数为______.97.5° 5．如图所示，把一副三角板叠放在一起，则∠ACD＝________°. 15 6．将一个圆分割成六个扇形，它们圆心角度数之间的关系为2∶3∶4∶6∶7∶8，则这五个扇形中圆心角最大的度数是________． 96° 7.如图，∠AOB＝∠COD＝90°，OC是∠AOB的平分线，OE是∠BOD的三等分线，试求∠COE的度数．基本平面图形直线线段线段的中点角的定义性质射线角角平分线定义对角线正多边形圆定义弧扇形圆心角多边形1.从课后习题中选取；2.完成练习册本课时的习题。