高中数学人教B版 (2019)必修 第四册11.4.2 平面与平面垂直精品ppt课件

这是一份高中数学人教B版 (2019)必修 第四册11.4.2 平面与平面垂直精品ppt课件，共21页。PPT课件主要包含了探究1二面角，二面角，半平面，线面垂直，面面垂直的判定方法，定义法，线线垂直，判定定理，要证两个平面垂直，线面垂直线线垂直等内容，欢迎下载使用。

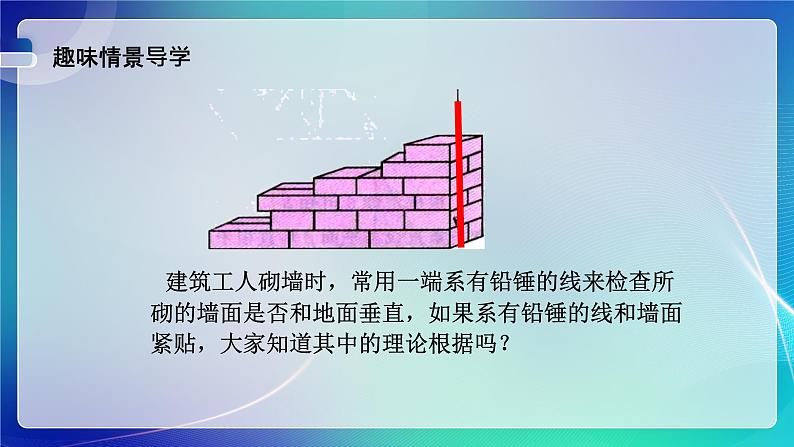
建筑工人砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直，如果系有铅锤的线和墙面紧贴，大家知道其中的理论根据吗？
1.掌握两个平面垂直的判定定理、性质定理.（重点）2.能利用两个定理解决简单的证明问题.（难点）3.使学生体会“类比归纳”思想在解决数学问题上的作用.
思考1：如图所示，笔记本电脑在打开的过程中，会给人以面面“夹角”变大的感觉，（1）观察电脑的打开过程，可以抽象出什么几何图形？动手画出抽象出的几何图形.（2）观察抽象出的几何图形，它由哪些几何元素构成？
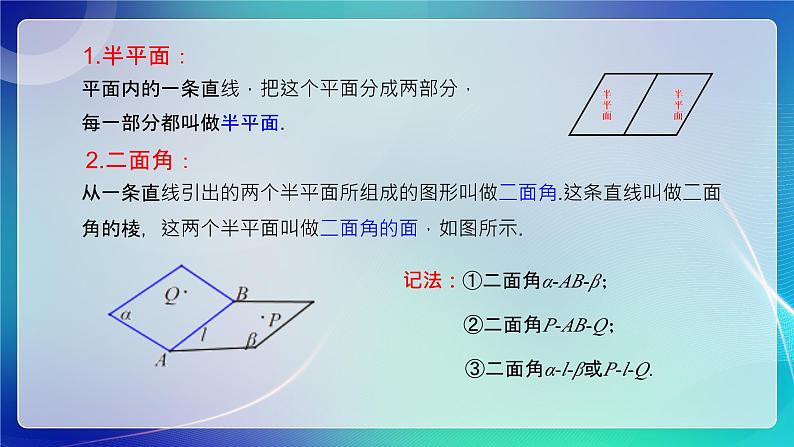
平面内的一条直线，把这个平面分成两部分，每一部分都叫做半平面.
从一条直线引出的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个半平面叫做二面角的面，如图所示.
记法：①二面角α-AB-β；
②二面角P-AB-Q；
③二面角α-l-β或P-l-Q.
思考2：观察教室门的开关过程，二面角是哪个角？
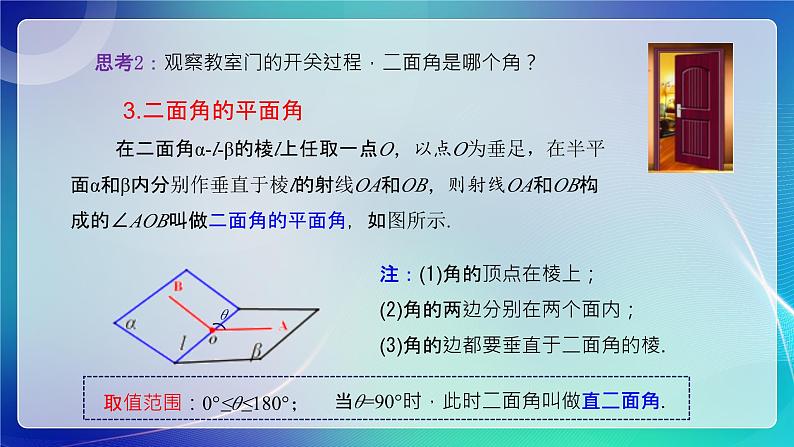
3.二面角的平面角 在二面角α-l-β的棱l上任取一点O，以点O为垂足，在半平面α和β内分别作垂直于棱l的射线OA和OB，则射线OA和OB构成的∠AOB叫做二面角的平面角，如图所示.
注：(1)角的顶点在棱上；(2)角的两边分别在两个面内；(3)角的边都要垂直于二面角的棱.
取值范围：0°≤θ≤180°；
当θ=90°时，此时二面角叫做直二面角.
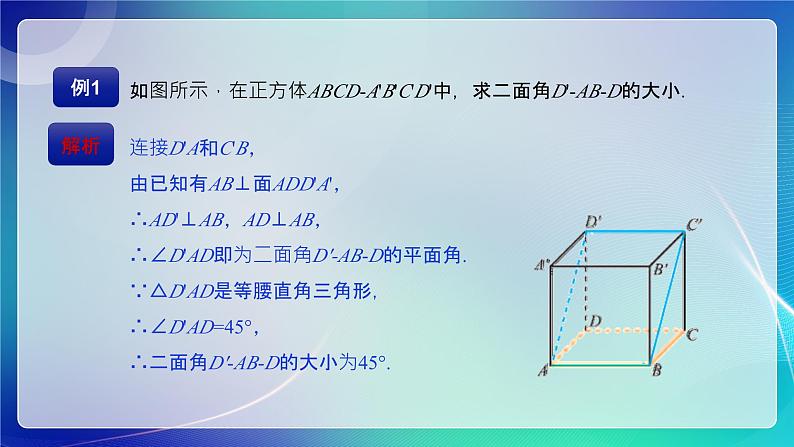
连接D'A和C'B，由已知有AB⊥面ADD'A'，∴AD'⊥AB，AD⊥AB，∴∠D'AD即为二面角D'-AB-D的平面角.∵△D'AD是等腰直角三角形，∴∠D'AD=45°，∴二面角D'-AB-D的大小为45°.
如图所示，在正方体ABCD-A'B'C'D'中，求二面角D'-AB-D的大小.
探究2 平面与平面垂直
思考1： 生活中有很多平面与平面垂直的例子，什么是平面与平面垂直？怎样来定义？
1. 平面与平面垂直：一般地，如果两个平面α与β所成角的大小90°，则称这两个平面互相垂直，记作α⊥β.
思考2：除了定义，还有没有更为简单的判定平面与平面垂直的方法？现在你知道用一端系有铅锤的线来检查所砌的墙面是否和地面垂直的道理了吗？
2.平面与平面垂直判定定理：
简记：线面垂直，则面面垂直.
如果一个平面过另一个平面的一条 ，则两个平面互相垂直.
证明：当l⊂α，l⊥β时，α与β一定相交.如图所示，设α∩β=m，l∩β=O.过O在平面β内作与m垂直的直线OA，则有l⊥OA,从而可知α与β所成角的大小为90°，因此α⊥β.
两个相交的平面的交线与第三个平面垂直
原来的两个平面与第三个平面的交线互相垂直
另一个平面的一条垂线.
只要在其中一个平面内找到
（线面垂直面面垂直）
思考3：如图所示，α⊥β，α∩β=m，AO⊂α，AO⊥m，垂足为O，则AO与β的位置关系是怎样的？说明理由.
证明：如图所示，过O在平面β内作与m垂直的直线OB,则∠AOB为二面角A-m-B的平面角.因为α⊥β,所以∠AOB=90°，因此AO⊥OB又因为AO⊥m，m∩OB=O，m⊂B且OB⊂B，所以AO⊥β.
3.面面垂直的性质定理：
如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
1.面面垂直线面垂直；
2.平面 ⊥平面β，要过平面 内一点引平面β的垂线
（线是一个平面内垂直于两平面交线的一条直线）
理解性质定理需把握住两点：
只需过这一点在平面 内作交线的垂线.
如图所示，己知α⊥β，在α与β的交线上取线段 且AC、BD分别在平面α和平面β内，它们都垂直于交线AB，并且AC=1，BD=2，求CD的长.
∵α⊥β，α∩β=AB，BD⊂β，BD⊥AB，∴BD⊥α，
又∵BC⊂α，∴BD⊥BC，∴△CBD是直角三角形.
如图,AB是☉O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC.(1)判断BC与平面PAC的位置关系,并证明.(2)判断平面PBC与平面PAC的位置关系.
解:(1)BC⊥平面PAC.证明：∵AB是☉O的直径，C是圆周上不同于A,B的任意一点，∴∠ACB=90°，∴BC⊥AC.又∵平面PAC⊥平面ABC，平面PAC∩平面ABC=AC,BC⊂平面ABC，∴BC⊥平面PAC.(2)∵BC⊂平面PBC，∴平面PBC⊥平面PAC.