山东省聊城市阳谷县2023-2024学年八年级上学期期中学业水平检测与反馈数学试卷(含解析)

这是一份山东省聊城市阳谷县2023-2024学年八年级上学期期中学业水平检测与反馈数学试卷(含解析)，共13页。

亲爱的同学，请你在答题之前，一定要仔细阅读以下说明：
1．试题由选择题与非选择题两部分组成．共150分．考试时间130分钟．
2．将姓名、准考证号、考场号、座号填写在答题卡指定的位置．
3．试题答案全部写在答题卡上，完全按照答题卡中的“注意事项”答题．考试结束，只交答题卡．
愿你放飞思维，认真审题，充分发挥，争取交一份圆满的答卷．
第Ⅰ卷 选择题（共48分）
一、选择题（共12小题，每小题4分，满分48分．每小题有且只有一个正确答案）
1. 下列四幅图案中，不是轴对称图形的是（ ）
A. B. C. D.
答案：D
解析：解：A．是轴对称图形，故本选项不合题意；
B．是轴对称图形，故本选项不合题意；
C．是轴对称图形，故本选项不合题意；
D．不是轴对称图形，故本选项符合题意．
故本题选：D．
2. 两个全等图形中可以不同的是（ ）
A. 位置B. 长度C. 角度D. 面积
答案：A
解析：两个全等图形中对应边的长度，对应角的角度，图形的面积相等，可以不同的是位置．
故选A．
3. 如图，已知图中的两个三角形全等，则的度数是( )

A. B. C. D.
答案：D
解析：
解析：解：两个三角形全等，
的度数是．
故选：D．
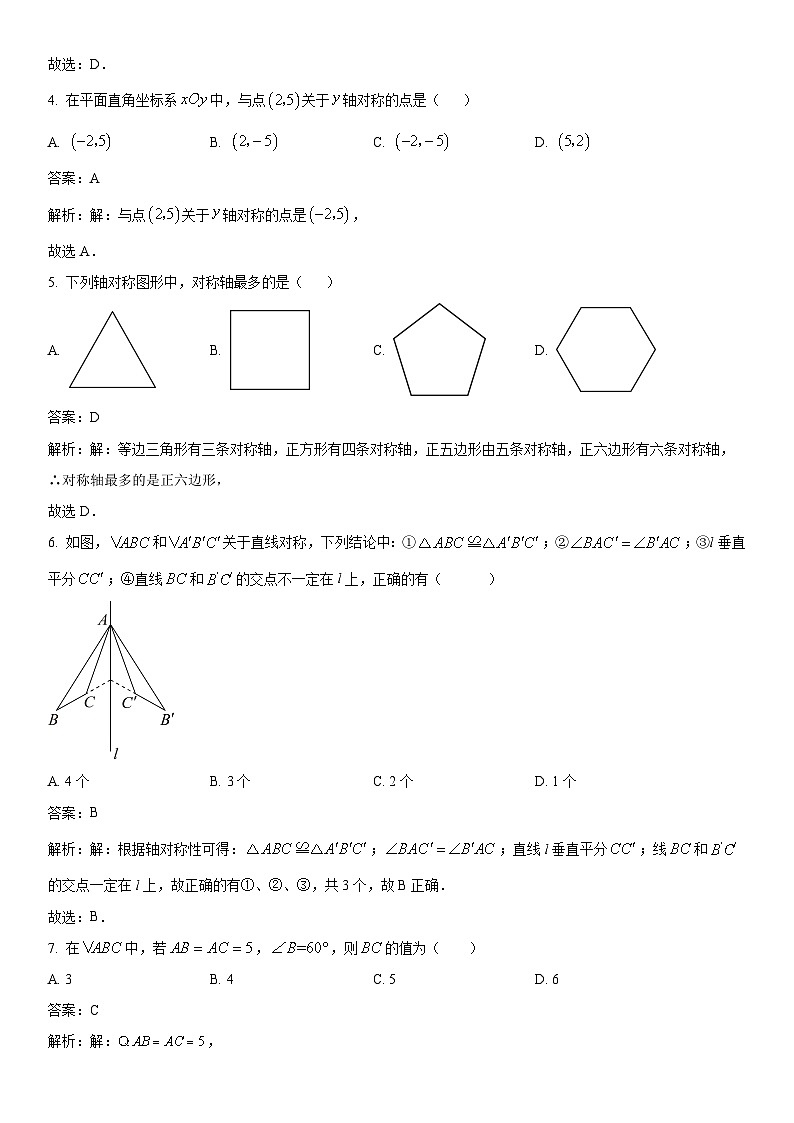
4. 在平面直角坐标系中，与点关于轴对称的点是（ ）
A. B. C. D.
答案：A
解析：解：与点关于轴对称的点是，
故选A．
5. 下列轴对称图形中，对称轴最多的是（ ）
A. B. C. D.
答案：D
解析：解：等边三角形有三条对称轴，正方形有四条对称轴，正五边形由五条对称轴，正六边形有六条对称轴，
∴对称轴最多的是正六边形，
故选D．
6. 如图，和关于直线对称，下列结论中：①；②；③l垂直平分；④直线和的交点不一定在l上，正确的有（ ）

A. 4个B. 3个C. 2个D. 1个
答案：B
解析：解：根据轴对称性可得：；；直线l垂直平分；线和的交点一定在l上，故正确的有①、②、③，共3个，故B正确．
故选：B．
7. 在中，若，，则的值为（ ）
A. 3B. 4C. 5D. 6
答案：C
解析：解：，
，
为等边三角形，
．
故选：C．
8. 如图，小明书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）
A. SSSB. SASC. SSAD. ASA
答案：D
解析：解：由图可知，三角形两角及夹边可以作出，
所以，依据是ASA．
故选：D．
9. 如图是一个平分角的仪器，其中，．将点放在角的顶点，和沿着角的两边放下，沿画一条射线，就是这个角的平分线．此仪器的原理是( )
A. B. C. D.
答案：A
解析：解：为公共边
在和中，
，
，
就是的平分线，
故选：A
10. 在中，根据下列尺规作图的痕迹，不能判断与大小关系的是（ ）
A. B.
C. D.
答案：D
解析：解：A．由作图痕迹，在上截取线段等于，则，所以A选项不符合题意；
B．由作图痕迹，在上延长线上截取线段等于，则，所以B选项不符合题意；
C．由作图痕迹，作的垂直平分线，可知，根据三角形三边关系得，即，所以C选项不符合题意；
D．由作图痕迹，作的垂直平分线，仿照C，可知，不能说明和的大小，所以D选项符合题意．
故选：D．
11. 如图，嘉琪任意剪了一张钝角三角形纸片（是钝角），他打算用折叠的方法折出的角平分线、边上的中线和高线，能折出的是（ ）

A. 边上的中线和高线B. 的角平分线和边上的高线
C. 的角平分线和边上的中线D. 的角平分线、边上的中线和高线
答案：C
解析：解：当与重合时，折痕是的角平分线；
当点A与点B重合时，折叠是的中垂线，
故选：C．
12. 如图，，，则下列结论错误的是（ ）

A. B.
C. D.
答案：D
解析：解：在和中，
，
，故选项A正确，不合题意；
，
，
，，
，
，
在和中，
，
，故选项B正确，不合题意；
，
，故选项C正确，不合题意；
，
，证不出，
∴选项D错误，符合题意；
故选：D．
二、填空题（共6小题，每小题4分，满分24分）
13. 要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有，如果圆形工件恰好通过卡钳，则此工件的外径必是之长了，其中的依据是全等三角形的判定条件______．
答案：
解析：解：连接，如图所示：
∵，
∴
故
故答案为：
14. 如图，将长方形纸片折叠成如图的形状，，则______．

答案：##103度
解析：解：由折叠的性质可得：，
∵，，
∴，
∵，
∴，
∴；
故答案为：
15. 数学在我们的生活中无处不在，就连小小的台球桌上都有数学问题，如图所示，，若，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证为______．

答案：
解析：解：∵，，
∴，
∵，
∴，
故答案为：
16. 如图，在中，，，通过观察尺规作图的痕迹，的度数是_____________．
答案：##85度
解析：解：由题意知：是线段的中垂线，是的角平分线，
∴，
∵，，
∴，
∴，
∴，
∴；
故答案为：．
17. 如图，在△ABC中，DE是AC的垂直平分线，AC=6cm，且△ABD的周长为13cm，则△ABC的周长为_____
答案：19cm##19厘米
解析：解：∵DE是AC的垂直平分线，
∴AD=CD，
∵△ABD的周长为13cm，
∴AB+BD+AD= AB+BD+CD =13cm，
∵AC=6cm，
∴△ABC的周长=AB+BD+CD+AC=13+6=19cm，
故答案为：19cm．
18. 在△ABC中，∠A＝80°，当∠B＝_____时，△ABC是等腰三角形．
答案：20°或50°或80°
解析：∵，
∴①当是顶角, 时，△ABC是等腰三角形；
②当是顶角，∠B=（180°﹣80°）÷2=50°时，△ABC是等腰三角形；
③是顶角，∠B=180°﹣80°×2=20°时，△ABC是等腰三角形；
故答案为:80°或50°或20°
三、解答题（共8小题，满分78分，解答应写出必要的文字说明和解题步骤．）
19. 如图，．求证：．
答案：见解析
解析：证明：，
即．
在和中，
．
20. 如图，在中，为其角平分线，于点，于点，的面积是，，，求的长．
答案：
解析：解：为的平分线，，，
，
∵，
∴，
即，
解得：，
．
21. 如图，已知点，，，一条直线上，，，．
（1）求证：；
（2）若，，求的长．
答案：（1）见解析 （2）
小问1详解：
证明：∵，，，
∴，
∴，
∴；
小问2详解：
∵，
∴，
∴，
∴，
∴．
22. 一个等腰三角形的周长是．
（1）若腰长是底边长的2倍，求各边的长．
（2）若其中一条边的长是，求另外两条边的长．
答案：（1），，
（2），或，
小问1详解：
解：设底边长为，则腰长为，
∵三角形的周长是，
∴，
解得：，则，
∴这个等腰三角形的各边的长为：，，；
小问2详解：
解：①当底边长为时，
则腰长为：，
所以另外两边的长为，，且符合三角形三边关系定理；
②当腰长为时，
则底边长为：，
所以另外两边长为，，且符合三角形三边关系定理．
23. 如图，．
（1）求的度数；
（2）若，求证：．
答案：（1）∠DAE=30°；（2）见详解．
解析：（1）∵AB∥DE，
∴∠E=∠CAB=40°，
∵∠DAB=70°，
∴∠DAE=∠DAB-∠CAB=30°；
（2）由（1）可得∠DAE=∠B=30°，
又∵AE=AB，∠E=∠CAB=40°，
∴△DAE≌△CBA（ASA），
∴AD=BC．
24. 如图，，，是上一点．求证：．

答案：见解析
解析：证明：连接．
，
．
又点．在线段的垂直平分线上，
就是线段的垂直平分线．
．
．
．
即．
25. 如图，等边三角形，交AC于点D，交于点E．
（1）求证：是等边三角形．
（2）求证：．
答案：（1）见详解 （2）见详解
小问1详解：
在等边中有：，，
∵，
∴，，
∴，
∴是等边三角形；
小问2详解：
∵在等边中，，
∴是等边的中线，
∴，
∴，
∵是等边三角形，
∴，
∵，
∴．
26. 如图，做一个“U”字形框架，其中，、足够长，，，点M从点B出发，向点A运动，同时点N从点B出发，向点Q运动，点M、N运动速度之比为，当M、N两点运动到某一瞬间同时停止，此时在射线上取点C，使与全等，求此时线段的长是多少？

答案：或
解析：解：设，则，
∵，使与全等，可分两种情况：
情况一：当，时，
，，
，
解得：，
；
情况二：当，时，
，，
，
解得：，
，
综上所述，或．