最新人教版高中数学必修第一册第四章　函数应用 章末复习课（课件）

这是一份最新人教版高中数学必修第一册第四章　函数应用 章末复习课（课件），共25页。

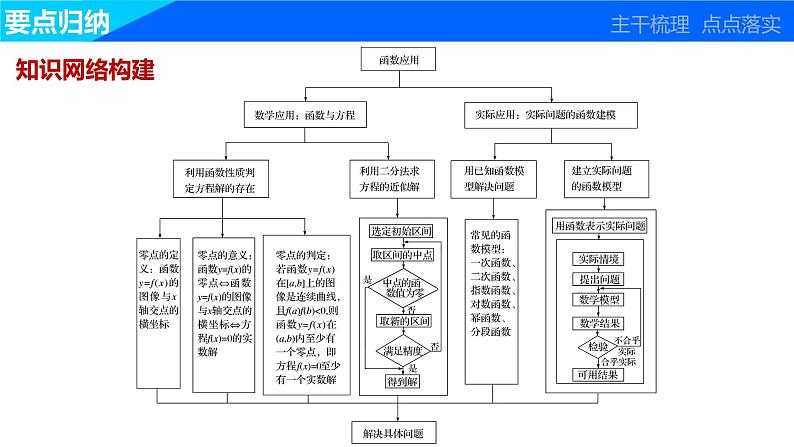
第四章　函数应用章末复习课1.体会函数与方程之间的联系，会用二分法求方程的近似解；2.了解指数函数、幂函数、对数函数的增长差异；3.巩固建立函数模型的过程和方法，了解函数模型的广泛应用.要点归纳题型探究达标检测学习目标要点归纳 　　　　主干梳理 点点落实知识网络构建知识方法回顾1.函数的零点与方程的根的关系：(1)方程f(x)＝0有实数根⇔函数 的图像与 有交点⇔ 有零点.(2)确定函数零点的个数有两个基本方法：①借助函数 性和 定理研究图像与x轴的交点个数；②通过移项，变形转化成 个函数图像的交点个数进行判断.答案y＝f(x)x轴函数y＝f(x)单调零点存在性两2.二分法(1)图像都在x轴同侧的函数零点 (填“能”或“不能”)用二分法求.(2)用二分法求零点近似解时，零点区间(a，b)始终要保持f(a)·f(b) 0；(3)若要求精度为0.01，则当|a－b| 0.01时，便可判断零点近似值为 .3.函数模型(1)给定函数模型与拟合函数模型中求函数解析式主要使用 法.(2)建立确定性的函数模型的基本步骤是__________________________________________.(3)所有的函数模型问题都应注意变量的实际意义对 的影响.返回答案不能<0，k是常数).(1)假设气体在半径为3 cm的管道中，流量速率为400 cm3/s，求该气体通过半径为r cm的管道时，其流量速率R的表达式；解　由题意，得R＝kr4(k是大于0的常数).由r＝3 cm，R＝400 cm3/s，得k·34＝400，解析答案(2)已知(1)中的气体通过的管道半径为5 cm，计算该气体的流量速率.解析答案即气体通过管道半径为5 cm时，该气体的流量速率约为3 086 cm3/s.反思与感悟　一旦选定函数模型，下面的工作就是挖掘题目条件求出待定系数.反思与感悟跟踪训练3　为了预防流感，某学校对教室用药熏消毒法进行消毒.已知药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比，药物释放完毕后，y与t的函数关系式为y＝ t－a(a为常数)，如图，根据图中所提供的信息，回答下列问题：(1)从药物释放开始，每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为_______________.解析　由题意和图示知，当0≤t≤0.1时，可设y＝kt(k为待定系数)，由于点(0.1,1)在直线上，∴k＝10；解析答案返回解析答案(2)据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过____小时后，学生才能回到教室.解析　由题意可得 得t>0.6，即至少需要经过0.6小时后，学生才能回到教室.0.61231.已知函数f(x)＝ax－x－a(a>0，a≠1)，那么函数f(x)的零点个数是(　　)A.0个 B.1个C.2个 D.至少1个解析　在同一坐标系中作出函数y＝ax与y＝x＋a的图像，当a>1时，如图(1)，当0