

数学第一册上册第二章 函数函数课后测评
展开一、选择题
1.函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x+\f(π,3)))的最小正周期为( )
A.eq \f(π,4) B.eq \f(π,2)
C.π D.2π
2.函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)-x))eq \b\lc\(\rc\)(\a\vs4\al\c1(x∈\b\lc\[\rc\](\a\vs4\al\c1(-\f(π,4),\f(π,4)))且x≠0))的值域为( )
A.[-1,1]
B.(-∞,-1]∪[1,+∞)
C.(-∞,1]
D.[-1,+∞)
3.函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,5)))的一个对称中心是( )
A.(0,0) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,5),0))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4π,5),0)) D.(π,0)
4.下列各式中正确的是( )
A.tan735°>tan800° B.tan1
A.eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(π,4),\f(π,4))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(\r(2),2),\f(\r(2),2)))
C.[-tan1,tan1] D.[-1,1]
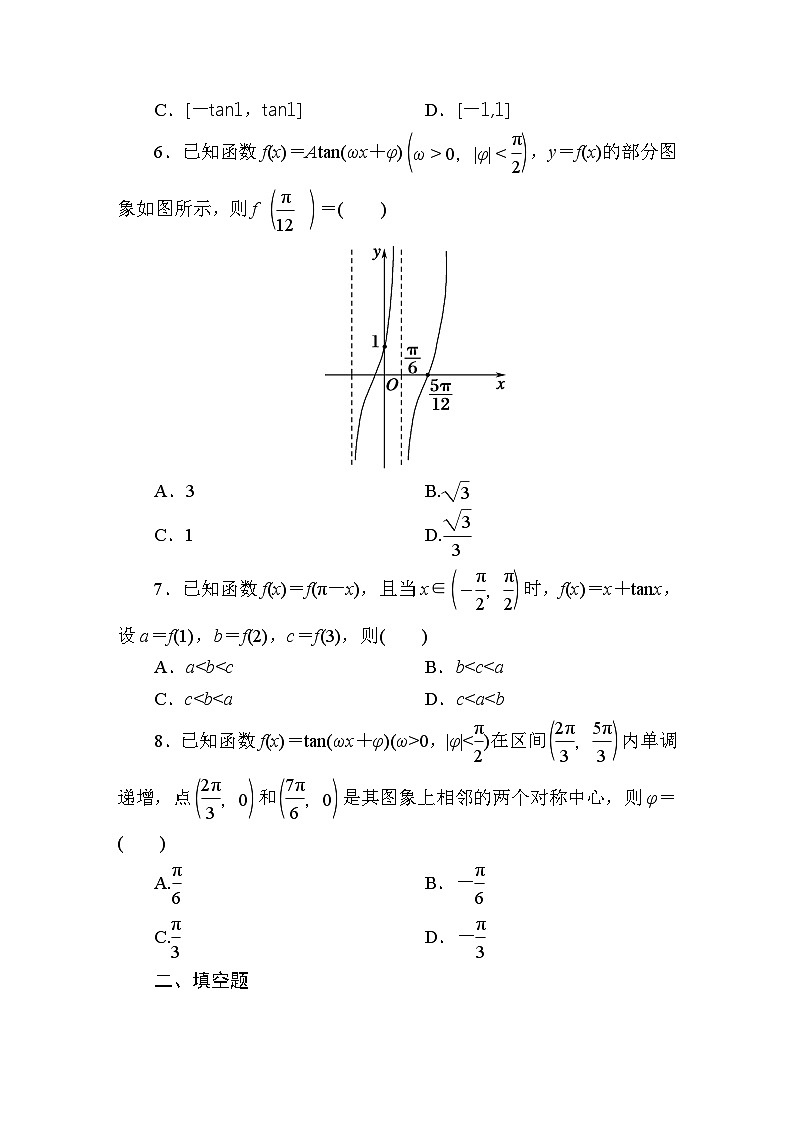
6.已知函数f(x)=Atan(ωx+φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(ω>0,|φ|<\f(π,2))),y=f(x)的部分图象如图所示,则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))=( )
A.3 B.eq \r(3)
C.1 D.eq \f(\r(3),3)
7.已知函数f(x)=f(π-x),且当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2)))时,f(x)=x+tanx,设a=f(1),b=f(2),c=f(3),则( )
A.a
C.eq \f(π,3) D.-eq \f(π,3)
二、填空题
9.函数f(x)=taneq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,6)))的定义域是
10.已知函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=eq \f(π,4)所得线段长为eq \f(π,4),则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))的值为 .
三、解答题
11.画出函数y=|tanx|+tanx的图象,并根据图象求出函数的值域、周期和单调区间.
12.已知x∈eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(π,3),\f(π,4))),f(x)=tan2x+2tanx+2,求f(x)的最大值和最小值,并求出f(x)取最大值和最小值时相应的x值.
13.(多选题)下列各项中,是函数f(x)=taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))-1在(0,π)上的零点的是( )
A.eq \f(π,24) B.eq \f(π,12)
C.eq \f(7π,24) D.eq \f(13π,24)
14.(多选题)已知函数f(x)=tanx,对任意x1,x2∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2)))(x1≠x2),给出下列结论,正确的是( )
A.f(x1+π)=f(x1)
B.f(-x1)=f(x1)
C.eq \f(fx1-fx2,x1-x2)>0
D.f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x1+x2,2)))>eq \f(fx1+fx2,2)(x1x2>0)
15.已知函数f(x)=asineq \b\lc\(\rc\)(\a\vs4\al\c1(kx+\f(π,3))),g(x)=btaneq \b\lc\(\rc\)(\a\vs4\al\c1(kx-\f(π,3)))(k>0),它们的周期之和为eq \f(3π,2),且f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))=geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2))),f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))=-eq \r(3)·geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))+1,则f(x)= ;g(x)的单调递增区间为 .
16.已知函数f(x)=x2+2xtanθ-1,x∈[-1,eq \r(3)],其中θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2))).
(1)当θ=-eq \f(π,6)时,求函数的最大值和最小值;
(2)求θ的取值范围,使y=f(x)在区间[-1,eq \r(3)]上是单调函数.
课时作业50 正切函数的性质与图象【解析版】
时间:45分钟
一、选择题
1.函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x+\f(π,3)))的最小正周期为( D )
A.eq \f(π,4) B.eq \f(π,2)
C.π D.2π
解析:函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x+\f(π,3)))的最小正周期为eq \f(π,\f(1,2))=2π.
2.函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)-x))eq \b\lc\(\rc\)(\a\vs4\al\c1(x∈\b\lc\[\rc\](\a\vs4\al\c1(-\f(π,4),\f(π,4)))且x≠0))的值域为( B )
A.[-1,1]
B.(-∞,-1]∪[1,+∞)
C.(-∞,1]
D.[-1,+∞)
解析:∵-eq \f(π,4)≤x≤eq \f(π,4)且x≠0,
∴eq \f(π,4)≤eq \f(π,2)-x≤eq \f(3π,4)且eq \f(π,2)-x≠eq \f(π,2),
∴值域为(-∞,-1]∪[1,+∞).
3.函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,5)))的一个对称中心是( C )
A.(0,0) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,5),0))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4π,5),0)) D.(π,0)
解析:令x+eq \f(π,5)=eq \f(kπ,2)(k∈Z),得x=eq \f(kπ,2)-eq \f(π,5),k∈Z,∴函数y=taneq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,5)))的对称中心是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)-\f(π,5),0))(k∈Z).令k=2,可得函数的一个对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4π,5),0)).
4.下列各式中正确的是( D )
A.tan735°>tan800° B.tan1
A.eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(π,4),\f(π,4))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(\r(2),2),\f(\r(2),2)))
C.[-tan1,tan1] D.[-1,1]
解析:∵-1≤sinx≤1,
而-eq \f(π,2)<-1≤sinx≤1
即函数值域为[-tan1,tan1].
6.已知函数f(x)=Atan(ωx+φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(ω>0,|φ|<\f(π,2))),y=f(x)的部分图象如图所示,则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))=( A )
A.3 B.eq \r(3)
C.1 D.eq \f(\r(3),3)
解析:由题意知,eq \f(T,2)=eq \f(5π,12)-eq \f(π,6)=eq \f(π,4),∴T=eq \f(π,2),
∴ω=eq \f(π,T)=2.又图象过点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,12),0)),
∴eq \f(5π,6)+φ=kπ,k∈Z,∴φ=kπ-eq \f(5π,6),k∈Z.
∵|φ|
∴feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))=eq \r(3)taneq \f(π,3)=3.故选A.
7.已知函数f(x)=f(π-x),且当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2)))时,f(x)=x+tanx,设a=f(1),b=f(2),c=f(3),则( D )
A.a
可得f(2)>f(1)>f(3),即b>a>c.故选D.
8.已知函数f(x)=tan(ωx+φ)(ω>0,|φ|
C.eq \f(π,3) D.-eq \f(π,3)
解析:正切曲线相邻两个对称中心的距离d=eq \f(T,2),∴函数f(x)的周期T=2d=2×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7π,6)-\f(2π,3)))=π,
即eq \f(π,ω)=π,解得ω=1,∴f(x)=tan(x+φ).
又∵函数f(x)=tan(x+φ)在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2π,3),\f(5π,3)))内单调递增,且eq \f(5π,3)-eq \f(2π,3)=π=T,
∴eq \f(2π,3)+φ=eq \f(π,2)+kπ,k∈Z,解得φ=kπ-eq \f(π,6),k∈Z.
又∵|φ|
9.函数f(x)=taneq \b\lc\(\rc\)(\a\vs4\al\c1(x+\f(π,6)))的定义域是{xeq \b\lc\|\rc\}(\a\vs4\al\c1(x≠kπ+\f(π,3),k∈Z)),f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))=eq \r(3).
解析:由题意知x+eq \f(π,6)≠kπ+eq \f(π,2)(k∈Z),即x≠kπ+eq \f(π,3)(k∈Z).故f(x)的定义域为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠kπ+\f(π,3),k∈Z)))),且feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))=taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)+\f(π,6)))=eq \r(3).
10.已知函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=eq \f(π,4)所得线段长为eq \f(π,4),则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))的值为0.
解析:∵f(x)的图象的相邻两支截直线y=eq \f(π,4)所得线段的长度即为f(x)=tanωx的一个周期,∴eq \f(π,ω)=eq \f(π,4),ω=4,因此feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))=taneq \b\lc\(\rc\)(\a\vs4\al\c1(4×\f(π,4)))=tanπ=0.
三、解答题
11.画出函数y=|tanx|+tanx的图象,并根据图象求出函数的值域、周期和单调区间.
解:由y=|tanx|+tanx知
y=eq \b\lc\{\rc\ (\a\vs4\al\c1(0,x∈\b\lc\(\rc\)(\a\vs4\al\c1(kπ-\f(π,2),kπ)),2tanx,x∈\b\lc\[\rc\)(\a\vs4\al\c1(kπ,kπ+\f(π,2)))))(k∈Z).
其图象如图所示.
所以值域:[0,+∞);周期性:T=π;
单调递增区间为eq \b\lc\[\rc\)(\a\vs4\al\c1(kπ,kπ+\f(π,2))),k∈Z.
12.已知x∈eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(π,3),\f(π,4))),f(x)=tan2x+2tanx+2,求f(x)的最大值和最小值,并求出f(x)取最大值和最小值时相应的x值.
解:f(x)=tan2x+2tanx+2=(tanx+1)2+1,
因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(-\f(π,3),\f(π,4))),所以tanx∈[-eq \r(3),1].
所以当tanx=-1,即x=-eq \f(π,4)时,f(x)有最小值,f(x)min=1;
当tanx=1,即x=eq \f(π,4)时,f(x)有最大值,f(x)max=5.
13.(多选题)下列各项中,是函数f(x)=taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))-1在(0,π)上的零点的是( AD )
A.eq \f(π,24) B.eq \f(π,12)
C.eq \f(7π,24) D.eq \f(13π,24)
解析:令f(x)=0得taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,6)))=1,
∴2x+eq \f(π,6)=eq \f(π,4)+kπ,k∈Z,解得x=eq \f(π,24)+eq \f(kπ,2),k∈Z.当k=0时,x=eq \f(π,24),当k=1时,x=eq \f(13π,24).故选AD.
14.(多选题)已知函数f(x)=tanx,对任意x1,x2∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2)))(x1≠x2),给出下列结论,正确的是( AC )
A.f(x1+π)=f(x1)
B.f(-x1)=f(x1)
C.eq \f(fx1-fx2,x1-x2)>0
D.f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x1+x2,2)))>eq \f(fx1+fx2,2)(x1x2>0)
解析:由于f(x)=tanx的周期为π,故A正确;函数f(x)=tanx为奇函数,故B不正确;C表明函数为增函数,而f(x)=tanx为区间eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2)))上的增函数,故C正确;由函数f(x)=tanx的图象可知,函数在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),0))上有feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x1+x2,2)))>eq \f(fx1+fx2,2),在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(π,2)))上有
feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x1+x2,2)))
解析:根据题意,可得
eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(2π,k)+\f(π,k)=\f(3π,2),,asin\b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)+\f(π,3)))=btan\b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)-\f(π,3))),,asin\b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,4)+\f(π,3)))=-\r(3)btan\b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,4)-\f(π,3)))+1,))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(k=2,,a=1,,b=\f(1,2),))故f(x)=sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x+\f(π,3))),
g(x)=eq \f(1,2)taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x-\f(π,3))).
令kπ-eq \f(π,2)<2x-eq \f(π,3)
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)-\f(π,12),\f(kπ,2)+\f(5π,12)))(k∈Z).
16.已知函数f(x)=x2+2xtanθ-1,x∈[-1,eq \r(3)],其中θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2))).
(1)当θ=-eq \f(π,6)时,求函数的最大值和最小值;
(2)求θ的取值范围,使y=f(x)在区间[-1,eq \r(3)]上是单调函数.
解:(1)当θ=-eq \f(π,6)时,
f(x)=x2-eq \f(2\r(3),3)x-1=eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(\r(3),3)))2-eq \f(4,3).
∵x∈[-1,eq \r(3)],
∴当x=eq \f(\r(3),3)时,f(x)取得最小值-eq \f(4,3),
当x=-1时,f(x)取得最大值eq \f(2\r(3),3).
(2)f(x)=(x+tanθ)2-1-tan2θ是关于x的二次函数,它的图象的对称轴为x=-tanθ.∵y=f(x)在区间[-1,eq \r(3)]上是单调函数,
∴-tanθ≤-1或-tanθ≥eq \r(3),
即tanθ≥1或tanθ≤-eq \r(3).
又θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(π,2),\f(π,2))),
∴θ的取值范围是
eq \b\lc\(\rc\](\a\vs4\al\c1(-\f(π,2),-\f(π,3)))∪eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(π,4),\f(π,2))).
高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质习题: 这是一份高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质习题,共4页。试卷主要包含了已知函数f=tan ),则等内容,欢迎下载使用。
人教A版 (2019)必修 第一册第五章 三角函数5.6 函数 y=Asin( ωx + φ)当堂达标检测题: 这是一份人教A版 (2019)必修 第一册第五章 三角函数5.6 函数 y=Asin( ωx + φ)当堂达标检测题,共7页。
高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课后作业题: 这是一份高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课后作业题,共8页。试卷主要包含了y=tanx2满足下列哪些条件,已知函数y=-2tan,则,故选C,下列各式正确的是,求函数y=3tan的定义域;等内容,欢迎下载使用。













