苏科版（2024）九年级下册6.5 相似三角形的性质多媒体教学课件ppt

这是一份苏科版（2024）九年级下册6.5 相似三角形的性质多媒体教学课件ppt，共43页。PPT课件主要包含了教学目标，相似三角形的性质，相似多边形的性质等内容，欢迎下载使用。
理解相似三角形周长之比、面积之比与相似比之间的关系
理解相似三角形对应高之比、对应中线之比、对应角平分线之比与相似比之间的关系
能借助相似三角形的性质去理解相似多边形的性质
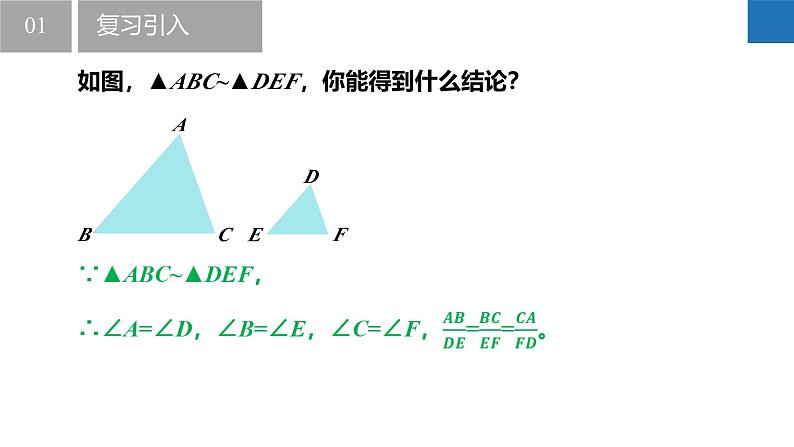
如图，▲ABC~▲DEF，你能得到什么结论？
【问题】相似三角形除了具有对应角相等、对应边成比例的性质外，还具有什么性质呢？
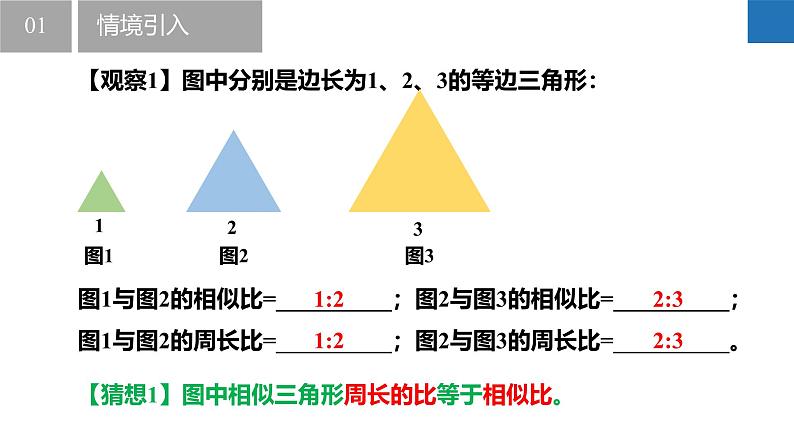
【观察1】图中分别是边长为1、2、3的等边三角形：
图1与图2的相似比=__________；图2与图3的相似比=__________；图1与图2的周长比=__________；图2与图3的周长比=__________。
【猜想1】图中相似三角形周长的比等于相似比。
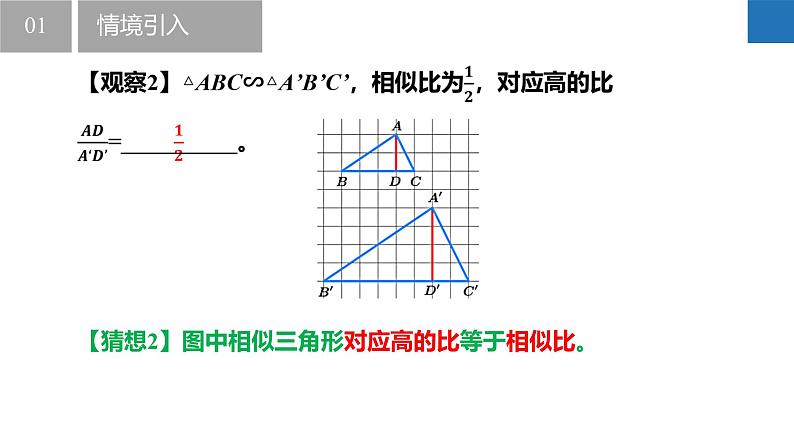
【猜想2】图中相似三角形对应高的比等于相似比。
【观察3】图中分别是边长为1、2、3的等边三角形：
图1与图2的相似比=__________；图2与图3的相似比=__________；图1与图2的面积比=__________；图2与图3的面积比=__________。
【猜想3】图中相似三角形面积的比等于相似比的平方。
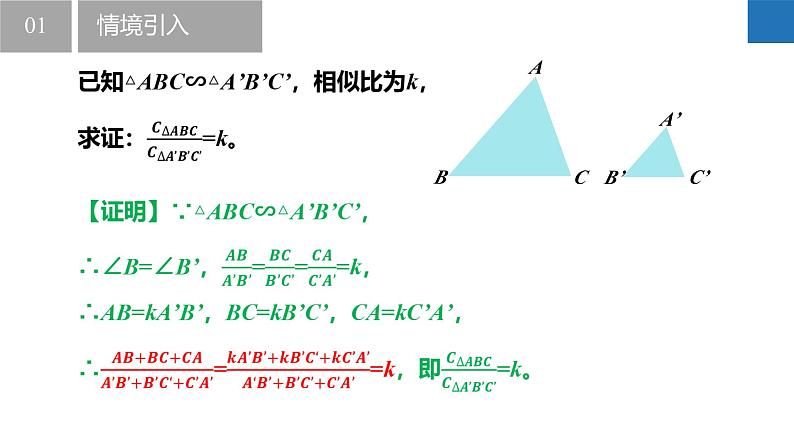
【证明】如图，作AD⊥BC交BC于点D，A’D’⊥B’C’交B’C’于点D’，
相似三角形周长的比等于相似比；相似三角形对应高的比等于相似比；相似三角形面积的比等于相似比的平方。
【问题】在上述探索过程中，我们发现“相似三角形对应高的比等于相似比”。类似地，相似三角形对应中线、对应角平分线等对应线段的比是否也等于相似比呢？
【猜想1】图中相似三角形对应中线的比等于相似比。
【猜想2】图中相似三角形对应角平分线的比等于相似比。
相似三角形对应中线的比等于相似比；相似三角形对应角平分线的比等于相似比。
推广：相似三角形对应线段的比等于相似比。
例1、已知△ABC与△A'B'C'相似，相似比为2:3；△A'B'C'与△A''B''C''相似，相似比为5:4，那么△ABC与△A''B''C''的相似比为（　　）A．5:6B．6:5C．15:8D．8:15
【分析】∵△ABC与△A′B′C′的相似比为2:3=10:15，△A′B′C′与△A″B″C″的相似比为5:4=15:12，∴△ABC与△A″B″C″相似比为10:12=5:6。
例2、(1)如图，已知△ADE∽△ACB，若AB=10，AC=8，AD=4，则AE的长是（　　）A．4 B．5 C．20 D．3.2
例3、(1)两个相似三角形的最短边分别为5cm和3cm，它们的周长之和为48cm，那么小三角形的周长为（　　）A．12cmB．18cmC．24cmD．30cm
【分析】由题意可得：两三角形的周长的比为5:3，设两三角形的周长分别为5xcm，3xcm，则5x+3x=48，解得：x=6，∴3x=18，即小三角形的周长为18cm。
例3、(2)两个相似三角形的最短边分别为5cm和3cm，它们的周长之差为12cm，那么大三角形的周长为（　　）A．12cmB．18cmC．24cmD．30cm
【分析】由题意可得：两三角形的周长的比为5:3，设两三角形的周长分别为5xcm，3xcm，则5x-3x=12，解得：x=6，∴5x=30，即大三角形的周长为30cm。
例4、如图，△ABC∽△A'B'C'，AD和A'D'分别是△ABC和△A′B′C′的高，若AD=2，A'D'=3，则△ABC与△A'B'C'的面积的比为（　　）A．4:9B．9:4C．2:3D．3:2
如图，五边形ABCDE~五边形A’B’C’D’E’，你能得到什么结论？
【问题】同样地，相似多边形除了具有对应角相等、对应边成比例的性质外，还具有什么性质呢？
Q1：如图，如果两个多边形相似，它们的周长有什么关系？
【猜想1】类比相似三角形，相似多边形周长的比等于相似比。
Q2：如图，如果两个多边形相似，它们的面积有什么关系？
【猜想2】类比相似三角形，相似多边形面积的比等于相似比的平方。
相似多边形周长的比等于相似比；相似多边形面积的比等于相似比的平方。
例1、如图，矩形ABCD∽矩形ADFE，AE=1，AB=4，则AD=（　　）A．2 B．2.4 C．2.5 D．3
例2、下列说法错误的是（　　）A．若把一个多边形的各边扩大为原来的k倍，则其周长也扩大为原来的k倍B．若把一个多边形的面积扩大为原来的k倍，则其各边扩大为原来的k2倍C．相似三角形的对应中线、对应角平分线、对应高的比都等于相似比D．相似三角形的面积比等于周长比的平方
例3、(1)若两个相似多边形的面积比为9:64，则它们的周长比为（　　）A．8:3B．3:8C．9:64D．64:9
例3、(2)若两个相似多边形的面积之比为1:4，周长之差为6，则这两个相似多边形的周长分别是__________。
【分析】∵两个相似多边形的面积之比为1:4，∴两个相似多边形的周长之比为1:2，设两个多边形的周长分别为x，x+6，则x+6=2x，解得：x=6，∴这两个相似多边形的周长分别是6，12。