高中数学沪教版（2020）选择性必修第二册第8章 成对数据的统计分析8.3 2x2列联表2 独立检验的具体应用优秀课时作业

这是一份高中数学沪教版（2020）选择性必修第二册第8章 成对数据的统计分析8.3 2x2列联表2 独立检验的具体应用优秀课时作业，文件包含沪教版2020高中数学选择性必修第二册83《2✖2列联表》分层练习原卷版docx、沪教版2020高中数学选择性必修第二册83《2✖2列联表》分层练习解析版docx等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。
一、单选题
1．（2022春·上海黄浦·高二上海市大同中学校考期末）某地政府调查育龄妇女生育意愿与家庭年收入高低的关系时，随机调查了当地3000名育龄妇女，用独立性检验的方法处理数据，并计算得，则根据这一数据以及临界值表，判断育龄妇女生育意愿与家庭年收入高低有关系的可信度（ ）
参考数据如下：，.
A．低于B．低于C．高于D．高于
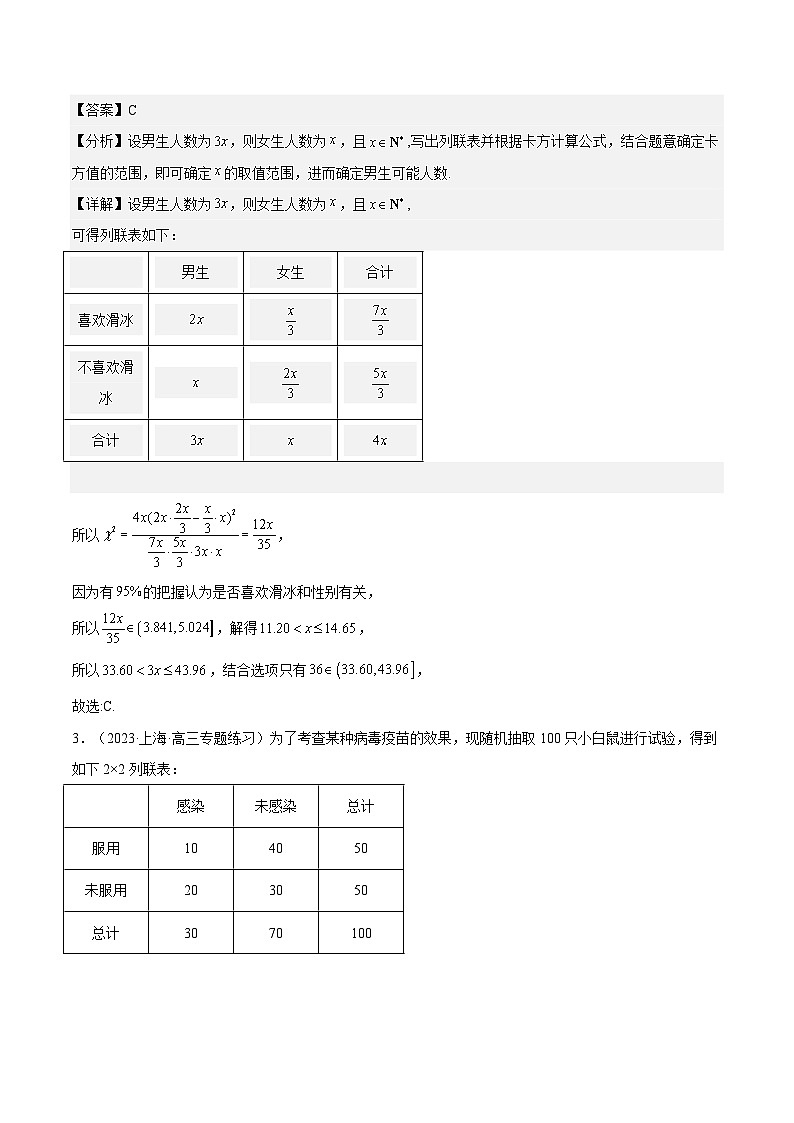
2．（2023春·上海杨浦·高三上海市杨浦高级中学校考开学考试）北京冬奥会的举办掀起了一阵冰雪运动的热潮．某高校在本校学生中对“喜欢滑冰是否与性别有关”做了一次调查，参与调查的学生中，男生人数是女生人数的倍，有的男生喜欢滑冰，有的女生喜欢滑冰．若根据独立性检验的方法，有的把握认为是否喜欢滑冰和性别有关，则参与调查的男生人数可能为（ ）
参考公式：，其中．
参考数据：
A．B．C．D．
3．（2023·上海·高三专题练习）为了考查某种病毒疫苗的效果，现随机抽取100只小白鼠进行试验，得到如下2×2列联表：
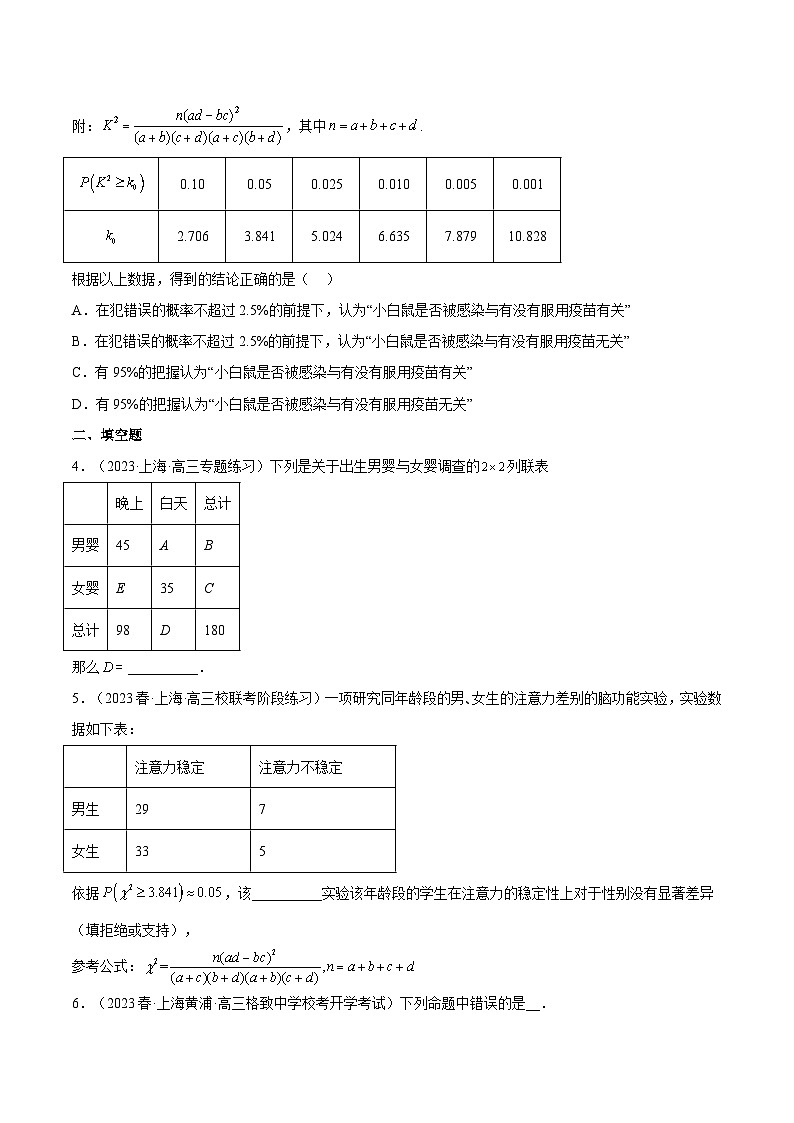
附：，其中.
根据以上数据，得到的结论正确的是（ ）
A．在犯错误的概率不超过2.5%的前提下，认为“小白鼠是否被感染与有没有服用疫苗有关”
B．在犯错误的概率不超过2.5%的前提下，认为“小白鼠是否被感染与有没有服用疫苗无关”
C．有95%的把握认为“小白鼠是否被感染与有没有服用疫苗有关”
D．有95%的把握认为“小白鼠是否被感染与有没有服用疫苗无关”
二、填空题
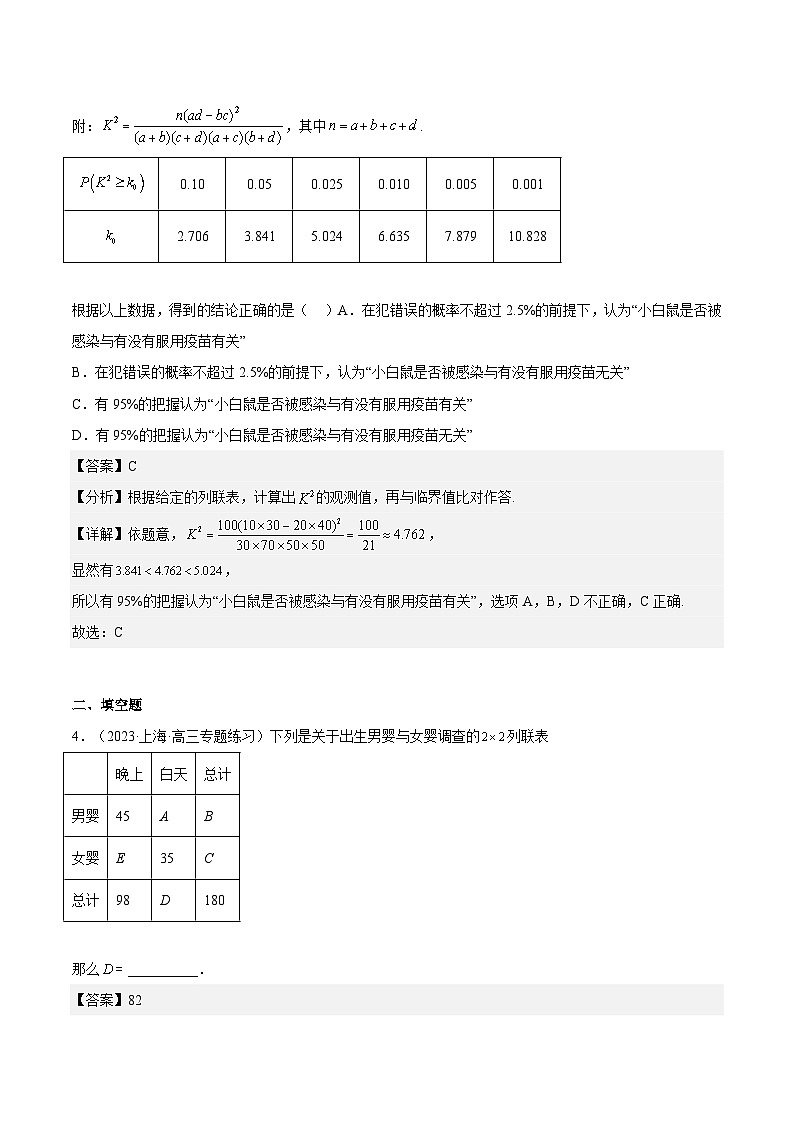
4．（2023·上海·高三专题练习）下列是关于出生男婴与女婴调查的列联表
那么__________．
5．（2023春·上海·高三校联考阶段练习）一项研究同年龄段的男､女生的注意力差别的脑功能实验，实验数据如下表：
依据，该__________实验该年龄段的学生在注意力的稳定性上对于性别没有显著差异（填拒绝或支持），
参考公式：
6．（2023春·上海黄浦·高三格致中学校考开学考试）下列命题中错误的是__．
①将一组数据中的每个数都加上或减去同一个常数后，均值与方差都不变；
②在一组样本数据（不全相等）的散点图中，若所有样本点都在直线上，则这组样本数据的线性相关系数为；
③在吸烟与患肺病这两个分类变量的计算中，若由独立性检验知，在犯错误率不超过0.01的前提下，认为吸烟与患肺病有关系．若某人吸烟，则他有的可能性患肺病．
三、双空题
7．（2022秋·上海虹口·高二华东师范大学第一附属中学校考期末）某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：
则有______%的把握认为男、女顾客对该商场服务的评价______（有或无）差异
附：
四、解答题
8．（2023·上海·高三专题练习）某农业兴趣小组针对两种肥料的作用进行对比试验，经过一季的试验后，对“使用肥料”和“使用肥料”的220株植物的生长情况进行研究，按照植株的高度大于或等于60厘米为“高株”，60厘米以下为“矮株”统计，得到如下的列联表：
(1)根据上面的列联表判断，能否有99.9%的把握认为“使用哪种肥料与植株高度”有关；
(2)为了进一步研究，从这批植物高株中用分层抽样的方法抽出6株，再从这6株中抽出3株，求抽到“使用肥料”植物的株数的分布列和数学期望.
附：
9．（2023·上海·高三专题练习）为了满足同学们多元化的需求，某校食堂每周开发一次新菜品，为了了解学生对新菜品的喜爱情况，他们采用给新菜品打分的方式（分数为整数，满分100分），在全校学生中随机选取1200名同学进行打分，发现所给数据均在内，现将这些数据分成6组并绘制出如图所示的样本频率分布直方图.
(1)请将样本频率分布直方图补充完整，并求出样本的平均数（同一组中的数据用该组区间的中点值作代表）；
(2)从这1200名同学中随机抽取，经统计其中有男同学70人，其中40人打分在，女同学中20人打分在，根据所给数据，完成上面的列联表，并在犯错概率不超过0.100的条件下，能否认为对新菜品的喜爱程度与性别有关（分数在内认为喜欢新菜品）？
附：，.
10．（2023·上海·高三专题练习）某工厂共有甲、乙两个车间，为了比较两个车间的生产水平，分别从两个车间生产的同一种零件中各随机抽取了100件，它们的质量指标值统计如下:
(1)估计该工厂生产这种零件的质量指标值的平均数;（同一组中的数据用该组区间的中点值作代表）
(2)根据所给数据，完成下面的列联表（表中数据单位:件），并判断是否有的把握认为甲、乙两个车间的生产水平有差异.
附:，其中.
11．（2022春·上海杨浦·高二复旦附中校考期末）为了更好地帮助高二学生准备生物地理的等级考试，复旦附中就“住校备考”还是“回家备考”问题进行了抽样调查，调查数据如下表（单位：人）：
(1)根据表中数据回答，能否有95%以上的把握判定是否回家备考与性别有关？
(2)从“回家备考”的11人中选出4人进行座谈，设参加座谈的男生人数为X，求X的分布和期望.
说明：解答本题，可以参考如下资料：
.
12．（2023春·上海闵行·高三闵行中学校考开学考试）某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图．
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5.0以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在名和名的学生进行了调查，得到右表中数据，根据表中的数据，能否在犯错的概率不超过0．05的前提下认为视力与学习成绩有关系?
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在的学生人数为，求的分布列和数学期望．
附：
．
13．（2022春·上海浦东新·高二上海市实验学校校考期中）在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人，女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.
(1)根据以上数据完成如下2×2的列联表；
(2)判断性别与休闲方式是否有关系.（显著性水平α取0.05）
【能力提升】
一、填空题
1．（2023·上海·高三专题练习）为了考察某种药物预防疾病的效果，进行动物试验，得到如下列联表：
若在本次考察中得出“在犯错误的概率不超过0.01的前提下认为药物有效”的结论，则a的最小值为___________（其中a≥40且a∈）（参考数据：≈2.58，≈3.29）
参考公式
临界值表
2．（2023·上海·高三专题练习）已知下列命题：
①在线性回归模型中，相关指数表示解释变量对于预报变量的贡献率，越接近于1，表示回归效果越好；
②两个变量相关性越强，则相关系数的绝对值就越接近于1；
③在回归直线方程中，当解释变量每增加一个单位时，预报变量平均减少0.5个单位；
④对分类变量与，它们的随机变量的观测值来说，越小，“与有关系”的把握程度越大．其中正确命题的序号是__________．
二、解答题
3．（2023春·上海·高三校联考阶段练习）自2015年上海启动《上海绿道专项规划（2035）》至今上海已建成绿道总长度近1600公里．根据《上海市气态空间专项规划（2021—2035）》，到2035年，上海绿道总长度将超过2000公里．届时，绿道会像城市的毛细血管一样，延伸到市民生活的各个角落，绿荫卜的绿道（步道、骑行道）给市民提供了散步休憩、跑步骑行运动的生态空间．某一线品牌自行车制造商在布局线下自行车体验与销售店时随机调研了1000位市民，调研数据如表1所示．166位有意愿购买万元级运动自行车的受访者的年龄（单位：岁），在各区间内的频数记录如表2所示．
表1
表2
(1)试估计有意愿购买万元级运动自行车人群的平均年龄（结果精确到0.1岁）．
(2)将表1的2×2列联表中的数据补充完整，并判断是否有95%的把握认为“离家附近（2千米内）有骑行绿道与万元级运动自行车消费有关”？
附：，其中．
4．（2022春·上海普陀·高二曹杨二中校考期末）某市为调研本市学生体质情况，采用按性别分层抽样的方法进行调查，得到体质测试样本的统计数据（单位：人）如表：
(1)根据所给数据，完成下面列联表，并据此判断：能否有的把握认为该市学生体质测试是否达标与性别有关.（注：体质测试成绩为优秀､良好或及格则体质达标，否则不达标）
其中；
(2)体质测试成绩为优秀或良好则称体质测试成绩为优良，以样本数据中男､女生体质测试成绩优良的频率视为该市男､女生体质测试成绩优良的概率，在该市学生中随机选取1名男生，1名女生，设所选2人中体质测试成绩优良人数为，求的分布列，数学期望与方差.
5．（2022春·上海金山·高二上海市金山中学校考期末）2021年9月，教育部印发《关于全面加强和改进新时代学校卫生与健康教育工作的意见》中指出：中小学生各项身体素质有所改善，大学生整体下降．某高校为提高学生身体素质，号召全校学生参加体育锻炼，结合“微信运动”APP每日统计运动情况，对每日平均运动10000步或以上的学生授予“运动达人”称号，低于10000步称为“参与者”，统计了200名学生在某月的运动数据，结果如下：
(1)完善列联表并说明：是否有99%的把握认为获得“运动达人”称号与性别有关?
(2)从全校运动“运动达人”中按性别分层抽取8人，再从8人中选取4人参加特训，将男生人数记为，求的分布列．
参考公式：．
6．（2022春·上海松江·高二上海市松江二中校考期末）第24届冬季奥运会将于2022年2月4日在北京开幕，本次冬季奥运会共设7个大项，15个分项，109个小项．为调查学生对冬季奥运会项目的了解情况，某大学进行了一次抽样调查，若被调查的男女生人数均为，统计得到以下列联表，经过计算可得．
(1)求的值，并判断有多大的把握认为该校学生对冬季奥运会项目的了解情况与性别有关；
(2)为弄清学生不了解冬季奥运会项目的原因，采用分层抽样的方法从抽取的不理解冬季奥运会项目的学生中随机抽取9人，再从这9人中抽取2人进行面对面交流，“至少抽到一名女生”的概率；
附表：
附：．
7．（2022秋·上海长宁·高三上海市延安中学校考期中）为加强环境保护，治理空气污染，环境检测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和SO2浓度（单位：μg/m3），得下表：
(1)估计事件“该市一天空气中PM2.5不超过75，且SO2浓度不超过150”的概率；
(2)根据所给数据，完成下面列联表，并判断是否有95%的把握认为该市一天中的PM2.5浓度与SO2浓度有关？
附表：
8．（2022秋·上海浦东新·高三华师大二附中校考阶段练习）为调查某小学学生的视力情况，随机抽取了该校150名学生（男生100人，女生50人），统计了他们的视力情况，结果如下：男生中有60人视力正常，女生中有40人视力正常.
(1)是否有99%的把握认为视力正常与否与性别有关？
(2)如果用这150名学生中，男生和女生视力正常的频率分别代替该校男生和女生视力正常的概率，且每位学生视力正常与否相互独立，现从该校学生中随机抽取3人（2男1女），设随机变量表示“3人视力正常”的人数，试求的分布列和数学期望.
附：.
9．（2022秋·上海黄浦·高三上海市向明中学校考开学考试）在统计调查中，问卷的设计是一门很大的学问，特别是对一些敏感性问题.例如学生在考试中有无作弊现象，社会上的偷税漏税等，更要精心设计问卷，设法消除被调查者的顾虑，使他们能够如实回答问题，否则被调查者往往会拒绝回答，或不提供真实情况.某调查中心为了调查中学生在考试中有无作弊现象，随机选取150名男学生和150名女学生进行问卷调查.问卷调查中设置了两个问题：①你是否为男生？②你是否在考试中有作弊现象.调查分两个环节，第一个环节：确定回答的问题，让被调查者从装有3个红球，3个黑球（除颜色外完全相同）的袋子中随机摸取两个球，摸到同色两球的学生如实回答第一个问题，摸到异色两球的学生如实回答第二个问题.第二个环节：填写问卷（问卷中不含问题，只有“是”与“否”）.已知统计问卷中有70张答案为“是”.
(1)根据以上的调查结果，利用你所学的知识，估计中学生在考试中有作弊现象的概率；
(2)据核实，以上的300名学生中有20名学生在考试中有作弊现象，其中男生15人，女生5人，试判断是否有97.5%的把握认为中学生在考试中有无作弊现象与性别有关.
参考公式和数据如下：，.
感染
未感染
总计
服用
10
40
50
未服用
20
30
50
总计
30
70
100
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
晚上
白天
总计
男婴
45
A
B
女婴
E
35
C
总计
98
D
180
注意力稳定
注意力不稳定
男生
29
7
女生
33
5
满意
不满意
男顾客
40
10
女顾客
30
20
0.050
0.010
0.001
k
3.841
6.635
10.828
高株
矮株
合计
使用肥料
20
90
110
使用肥料
40
70
110
合计
60
160
220
0.10
0.05
0.010
0.005
0.001
2.706
3.841
6.635
7.879
10.828
喜欢
不喜欢
合计
男同学
女同学
合计
（）
0.100
0.050
0.010
0.001
2.706
3.841
6.635
10.828
质量指标值
甲车间（件）
15
20
25
31
9
乙车间（件）
5
10
15
39
31
合计
甲车间
乙车间
合计
0.05
0.01
0.001
k
3.841
6.635
10.828
住校备考
回家备考
合计
男
4
8
12
女
10
3
13
合计
14
11
25
0.25
0.15
0.10
0.05
0.01
k
1.323
2.072
2.706
3.841
6.635
年级名次
是否近视
1~50
951~1000
近视
41
32
不近视
9
18
0.100
0.050
0.025
0.010
0.005
k
2.706
3.841
5.624
6.635
7.879
休闲方式性别
看电视
运动
总计
女
男
总计
药物
疾病
合计
未患病
患病
服用
a
50-a
50
未服用
80-a
a-30
50
合计
80
20
100
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
有意愿购买万元级运动自行车
没有意愿购买万元级运动自行车
总计
距家2千米内有骑行绿道
118
270
距家2千米内无骑行绿道
总计
166
1000
年龄分组区间
频数
16
24
35
30
21
15
11
6
5
3
0.10
0.05
0.01
0.005
k
2.706
3.841
6.635
7.879
优秀
良好
及格
不及格
男生
100
200
780
120
女生
120
200
520
120
达标
不达标
合计
男生
女生
合计
运动达人
参与者
合计
男生
70
女生
80
合计
80
200
2.072
2.706
3.841
6.635
7.879
10.828
0.15
0.10
0.05
0.010
0.005
0.001
男生
女生
合计
了解
不了解
合计
0.10
0.05
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828

[0,50]
[0,35]
32
18
4
(35,75]
6
8
12
(75,115]
3
7
10

[0,150]
(150,475]
合计
[0,75]
(75,115]
合计
0.1
0.05
0.01
0.005
0.001
k
2.706
3.841
6.635
7.879
10.828
0.15
0.10
0.05
0.025
0.005
2.072
2.706
3.841
5.024
7.879