江西省吉安市第四中学2024-2025学年数学九年级第一学期开学质量跟踪监视试题【含答案】

这是一份江西省吉安市第四中学2024-2025学年数学九年级第一学期开学质量跟踪监视试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知直角三角形的两直角边长分别为5和12，则此直角三角形斜边上的中线长为（）
A．B．6C．13D．
2、（4分）下列各组数中，以它们为边的三角形是直角三角形的是（ ）
A．1，2，3B．9，16，25C．12，15，20D．1，2，
3、（4分）整数满足，则的值为
A．4B．5C．6D．7
4、（4分）在▱ABCD中，已知∠A=60°，则∠C的度数是（ ）
A．30°B．60°C．120°D．60°或120°
5、（4分）等边△ABC的边长为6，点O是三边垂直平分线的交点，∠FOG=120°，∠FOG的两边OF，OG分别交AB，BC与点D，E，∠FOG绕点O顺时针旋转时，下列四个结论正确的是（ ）
①OD=OE；②；③；④△BDE的周长最小值为9.
A．1个B．2个C．3个D．4个
6、（4分）下列判断中，错误的是（ ）
A．方程是一元二次方程B．方程是二元二次方程
C．方程是分式方程D．方程是无理方程
7、（4分）如图，在等边△ABC中，点P从A点出发，沿着A→B→C的路线运动，△ACP的面积为S，运动时间为t，则S与t的图像是（ ）
A．B．
C．D．
8、（4分）在平面直角坐标系中，点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）将一个有80个数据的一组数分成四组，绘出频数分布直方图，已知各小长方形的高的比为，则第二小组的频数为______.
10、（4分）既是轴对称图形，又是中心对称图形的四边形是______．
11、（4分）小明从A地出发匀速走到B地.小明经过（小时）后距离B地（千米）的函数图像如图所示.则A、B两地距离为_________千米.
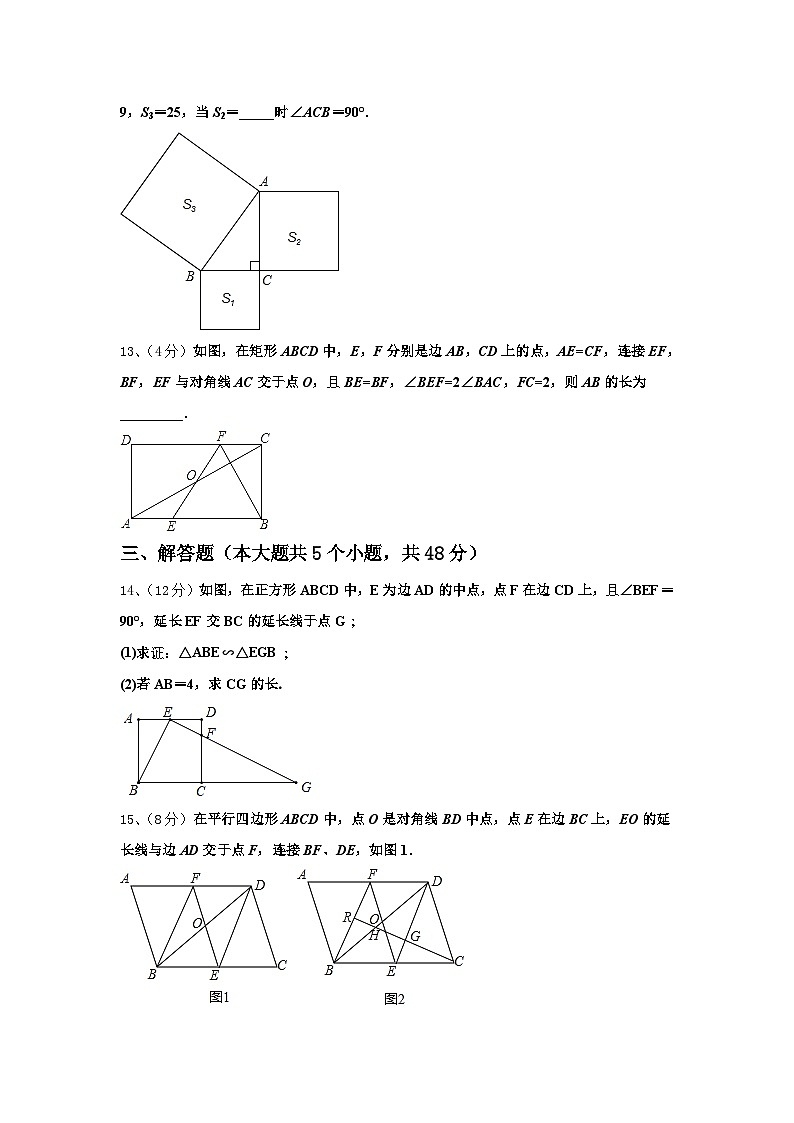
12、（4分）如图，以△ABC的三边为边向外作正方形，其面积分别为S1，S2，S3，且S1＝9，S3＝25，当S2＝_____时∠ACB＝90°．
13、（4分）如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为_________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且∠BEF＝90°，延长EF交BC的延长线于点G；
(1)求证：△ABE∽△EGB；
(2)若AB＝4，求CG的长.
15、（8分）在平行四边形ABCD中，点O是对角线BD中点，点E在边BC上，EO的延长线与边AD交于点F，连接BF、DE，如图1．
（1）求证：四边形BEDF是平行四边形；
（2）在（1）中，若DE＝DC，∠CBD＝45°，过点C作DE的垂线，与DE、BD、BF分别交于点G、H、R，如图2．
①当CD＝6，CE＝4时，求BE的长．
②探究BH与AF的数量关系，并给予证明．
16、（8分）如图，AD 是△ABC 的角平分线，M 是 BC 的中点， FM∥AD 交 BA 的延长线于点 F，交 AC 于点 E．求证：
（1）CE=BF．
（2）AB+AC=2CE．
17、（10分）计算(1)(+)(﹣)
(2)2﹣6+3
18、（10分）解方程：-=2
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）计算：．
20、（4分）将边长分别为2、3、5的三个正方形按图所示的方式排列，则图中阴影部分的面积为 ．
21、（4分）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为 （用n表示）
22、（4分）若一组数据1，3，，5，4，6的平均数是4，则这组数据的中位数是__________.
23、（4分）如图所示，某人在D处测得山顶C的仰角为30°，向前走200米来到山脚A处，测得山坡AC的坡度i=1∶0.5，则山的高度为____________米.
二、解答题（本大题共3个小题，共30分）
24、（8分）先化简，再求值：其中
25、（10分）某校为了解全校学生上学期参加“生涯规划”社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
参加社区活动次数的频数、频率
根据以上图表信息，解答下列问题：
（1）表中a= ， b= ， m= ， n= .
（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
26、（12分）为了解某校九年级男生在体能测试的引体向上项目的情况，随机抽取了部分男生引体向上项目的测试成绩，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：
（Ⅰ）本次接受随机抽样调查的男生人数为 ，图①中m的值为 ；
（Ⅱ）求本次调查获取的样本数据的平均数、众数和中位数；
（Ⅲ）若规定引体向上6次及以上（含6次）为该项目良好，根据样本数据，估计该校320名九年级男生中该项目良好的人数．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
已知直角三角形的两直角边长分别为5和12，根据勾股定理求得斜边为13，根据直角三角形斜边上的中线等于斜边的一半，得此直角三角形斜边上的中线长为，故选D.
2、D
【解析】
根据勾股定理的逆定理，只需验证两小边的平方和是否等于最长边的平方即可．
【详解】
解：A、∵12＋22≠32，∴不能构成直角三角形，故本选项不符合题意；
B、∵92＋162≠252，∴不能构成直角三角形，故本选项不符合题意；
C、∵122＋152≠202，∴不能构成直角三角形，故本选项不符合题意；
D、∵12＋22＝2，∴能够构成直角三角形，故本选项符合题意．
故选：D．
点评：本题考查的是勾股定理的逆定理，即如果三角形的三边长a，b，c满足a2＋b2＝c2，那么这个三角形就是直角三角形．
3、A
【解析】
根据16＜24＜25，得出的取值范围，即可确定n的值．
【详解】
解：∵，且16＜24＜25，
∴4＜＜5，
∴n＝4，
故选：A．
本题考查了估算无理数的大小，运用“夹逼法”是解决本题的关键．
4、B
【解析】
由平行四边形的对角相等即可得出答案．
【详解】
∵四边形ABCD是平行四边形，
∴∠C=∠A=60°；
故选：B．
本题考查了平行四边形的性质；熟练掌握平行四边形的对角相等是解题的关键．
5、B
【解析】
连接OB、OC，如图，利用等边三角形的性质得∠ABO=∠OBC=∠0CB=30°，再证明∠BOD=∠COE，于是可判断△BOD≌△COE，所以BD=CE，OD=OE，则可对①进行判断；利用 得到四边形ODBE的面积 ，则可对进行③判断；作OH⊥DE，如图，则DH=EH，计算出=，利用面积随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断；由于△BDE的周长=BC+DE=4+DE=4+OE，根据垂线段最短，当OE⊥BC时，OE最小，△BDE的周长最小，计算出此时OE的长则可对④进行判断.
【详解】
解：连接OB、OC，如图，
∵△ABC为等边三角形，
∴∠ABC=∠ACB=60°，
∵点0是△ABC的中心，
∴OB=OC，OB、OC分别平分∠ABC和∠ACB，
∴∠ABO=∠0BC=∠OCB=30°
∴∠BOC=120°，即∠BOE+∠COE=120°，而∠DOE=120°，即∠BOE+∠BOD=120°，
∴∠BOD=∠COE，
在△BOD和△COE中

∴△BOD2≌△COE，
∴BD=CE，OD=OE，所以①正确；
∴，
∴四边形ODBE的面积 ，所以③错误；
作OH⊥DE，如图，则DH=EH，
∵∠DOE=120°，
∴∠ODE=∠OEH=30°，
即S△ODE随OE的变化而变化，
而四边形ODBE的面积为定值，
所以②错误；
∵BD=CE，
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=6+OE，当OE⊥BC时，OE最小，△BDE的周长最小，此时OE=，
.△BDE周长的最小值=6+3=9，所以④正确.
故选：B.
本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等.也考查了等边三角形的性质和全等三角形的判定与性质.
6、D
【解析】
可以先判断各个选项中的方程是什么方程，从而可以解答本题.
【详解】
解：A、x(x-1)=0是一元二次方程，故A正确；
B、xy+5x=0是二元二次方程，故B正确；
C、是分式方程，故C正确；
D、是一元二次方程，故D错误.
故选D.
本题考查了各类方程的识别.
7、C
【解析】
当点A开始沿AB边运动到点B时，△ACP的面积为S逐渐变大；当点A沿BC边运动到点C时，△ACP的面积为S逐渐变小. , ∴由 到 与由 到 用的时间一样.故选C.
8、B
【解析】
应先判断出所求点P的横坐标、纵坐标的符号，进而判断其所在的象限．
【详解】
∵点P(−1,2)的横坐标−1<0，纵坐标2>0，
∴点P在第二象限。
故选：B.
此题考查点的坐标，难度不大
二、填空题（本大题共5个小题，每小题4分，共20分）
9、2
【解析】
各小长方形的高的比为3：3：2：3，就是各组频率的比，也是频数的比，根据一组数据中，各组的频率和等于3；各组的频数和等于总数，即可求解．
【详解】
∵各小长方形的高的比为3：3：2：3，
∴第二小组的频率=3÷（3+3+2+3）=0.3．
∵有80个数据，
∴第二小组的频数=80×0.3=2．
故答案为：2.
本题是对频率、频数意义的综合考查．
注意：各小组频数之和等于数据总和，各小组频率之和等于3．
10、矩形（答案不唯一）
【解析】
根据轴对称图形与中心对称图形的概念，写一个即可.
【详解】
解：矩形既是轴对称图形，又是中心对称图形.
故答案为：矩形(答案不唯一).
本题考查了轴对称图形与中心对称图形的概念.
11、20
【解析】
根据图象可知小明从A地出发匀速走到B地需要4小时，走3小时后距离B地5千米，所以小明的速度为5千米/时，据此解答即可．
【详解】
解：根据题意可知小明从A地出发匀速走到B地需要4小时，走3小时后距离B地5千米，所以小明的速度为5千米/时，
所以A、B两地距离为：4×5=20（千米）．
故答案为：20
本题考查了一次函数的应用，观察函数图象结合数量关系，列式计算是解题的关键．
12、1
【解析】
设△ABC的三边分别为BC=a、AC=b、AB=c，当∠ACB＝90°时，△ABC是直角三角形，由勾股定理可得到a2+b2＝c2，即S1+S2＝S3，代入可得解.
【详解】
设△ABC的三边分别为BC=a、AC=b、AB=c，
∴S1＝a2＝9，S2＝b2，S3＝c2＝25，
当∠ACB＝90°时，△ABC是直角三角形，
∴a2+b2＝c2，即S1+S2＝S3，
∴S2＝S3﹣S1＝1．
故答案为：1．
本题考查了勾股定理的几何背景，灵活运用勾股定理是解题关键.
13、6
【解析】
先证明△AOE≌△COF，Rt△BFO≌Rt△BFC，再证明△OBC、△BEF是等边三角形即可求出答案.
【详解】
如图，连接BO，
∵四边形ABCD是矩形，
∴DC∥AB，∠DCB=90°
∴∠FCO=∠EAO
在△AOE与△COF中，
∴△AOE≌△COF
∴OE=OF,OA=OC
∵BF=BE
∴BO⊥EF，∠BOF=90°
∵∠BEF=2∠BAC=∠CAB+∠AOE
∴∠EAO=∠EOA，
∴EA=EO=OF=FC=2
在Rt△BFO与Rt△BFC中
∴Rt△BFO≌Rt△BFC
∴BO=BC
在Rt△ABC中，∵AO=OC，
∴BO=AO=OC=BC
∴△BOC是等边三角形
∴∠BCO=60°，∠BAC=30°
∴∠FEB=2∠CAB=60°，
∵BE=BF
∴EB=EF=4
∴AB=AE+EB=2+4=6，
故答案为6.
本题考查的是全等三角形的性质与判定和等边三角形的判定与性质，能够充分调动所学知识是解题本题的关键.
三、解答题（本大题共5个小题，共48分）
14、 (1)证明见解析；(2)CG=6.
【解析】
(1)由正方形的性质与已知得出∠A＝∠BEG，证出∠ABE＝∠G，即可得出结论；
(2)由AB＝AD＝4，E为AD的中点，得出AE＝DE＝2，由勾股定理得出BE＝，由△ABE∽△EGB，得出，求得BG＝10，即可得出结果.
【详解】
(1)证明：∵四边形ABCD为正方形，且∠BEG＝90°，
∴∠A＝∠BEG，
∵∠ABE+∠EBG＝90°，∠G+∠EBG＝90°，
∴∠ABE＝∠G，
∴△ABE∽△EGB；
(2)∵AB＝AD＝4，E为AD的中点，
∴AE＝DE＝2，
在Rt△ABE中，BE＝，
由(1)知，△ABE∽△EGB，
∴，即：，
∴BG＝10，
∴CG＝BG﹣BC＝10﹣4＝6.
本题主要考查了四边形与相似三角形的综合运用，熟练掌握二者相关概念是解题关键
15、（1）详见解析；（2）①4﹣2；②AF＝BH，详见解析
【解析】
(1)由“ASA”可得△BOE≌△DOF，可得DF＝BE，可得结论；
(2)①由等腰三角形的性质可得EN＝CN＝2，由勾股定理可求DN，由等腰三角形的性质可求BN的长，即可求解；
②如图，过点H作HM⊥BC于点M，由“AAS”可证△HMC≌△CND，可得HM＝CN，由等腰直角三角形的性质可得BH＝HM，即可得结论．
【详解】
(1)证明：∵平行四边形ABCD中，点O是对角线BD中点，
∴AD∥BC，BO＝DO，
∴∠ADB＝∠CBD，且∠DOF＝∠BOE，BO＝DO，
∴△BOE≌△DOF（ASA）
∴DF＝BE，且DF∥BE，
∴四边形BEDF是平行四边形；
(2)①如图2，过点D作DN⊥EC于点N，
∵DE＝DC＝6，DN⊥EC，
∴EN＝CN＝2，
∴DN＝＝＝4，
∵∠DBC＝45°，DN⊥BC，
∴∠DBC＝∠BDN＝45°，
∴DN＝BN＝4，
∴BE＝BN﹣EN＝4﹣2；
故答案为：BE＝4﹣2.
②AF＝BH，
理由如下：如图，过点H作HM⊥BC于点M，
∵DN⊥EC，CG⊥DE，
∴∠CEG+∠ECG＝90°，∠DEN+∠EDN＝90°，
∴∠EDN＝∠ECG，
∵DE＝DC，DN⊥EC，
∴∠EDN＝∠CDN，EC＝2CN，
∴∠ECG＝∠CDN，
∵∠DHC＝∠DBC+∠BCH＝45°+∠BCH，∠CDB＝∠BDN+∠CDN＝45°+∠CDN，
∴∠CDB＝∠DHC，
∴CD＝CH，且∠HMC＝∠DNC＝90°，∠ECG＝∠CDN，
∴△HMC≌△CND（AAS）
∴HM＝CN，
∵HM⊥BC，∠DBC＝45°，
∴∠BHM＝∠DBC＝45°，
∴BM＝HM，
∴BH＝HM，
∵AD＝BC，DF＝BE，
∴AF＝EC＝2CN，
∴AF＝2HM＝BH．
故答案为：AF＝BH.
本题是四边形综合题，考查了平行四边形的性质，全等三角形的判定和性质，勾股定理，等腰直角三角形的性质，添加恰当辅助线构造全等三角形是本题的关键．
16、（1）见解析；（2）见解析
【解析】
（1）延长CA交FM的平行线BG于G点，利用平行线的性质得到BM=CM、CE=GE，从而证得CE=BF；
（2）利用上题证得的EA=FA、CE=BF，进一步得到AB+AC=AB+AE+EC=AB+AF+EC=BF+EC=2EC．
【详解】
解：（1）证明：延长CA交FM的平行线BG于G点，
则∠G=∠CAD，∠GBA=∠BAD，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴AG=AB，
∵FM∥AD
∴∠F=∠BAD、∠FEA=∠DAC
∵∠BAD=∠DAC，
∴∠F=∠FEA，
∴EA=FA，
∴GE=BF，
∴M为BC边的中点，
∴BM=CM，
∵EM∥GB，
∴CE=GE，
∴CE=BF；
（2）证明：∵EA=FA、CE=BF，
∴AB+AC=AB+AE+EC=AB+AF+EC=BF+EC=2EC．
本题考查了三角形的中位线定理，解题的关键是正确地构造辅助线，另外题目中还考查了平行线等分线段定理．
17、（1）2；（2）14
【解析】
（1）根据平方差公式可以解答本题；
（2）根据二次根式的加减法可以解答本题．
【详解】
解：（1）
＝5﹣3
＝2；
（2）
＝
＝．
本题考查二次根式的混合运算，解答本题的关键是明确二次根式混合运算的计算方法．
18、x=-1
【解析】
方程两边同时乘以最简公分母x2-4，把分式方程转化为整式方程求解.
【详解】
解：方程两边都乘以（x+2）（x-2）得：（x-1）（x+2）-4=2（x+2）（x-2），
即x2-x-2=0，
解得：x=-1或2，
检验：当x=-1时，（x+2）（x-2）≠0，所以x=-1是原方程的解，
当x=2时，（x+2）（x-2）=0，所以x=2不是原方程的解，
所以原方程组的解为：x=-1.
故答案为：x=-1.
本题考查了解分式方程.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
20、
【解析】
因为阴影部分的面积=S正方形BCQW﹣S梯形VBCF，根据已知求得梯形的面积即不难求得阴影部分的面积了．
解：∵VB∥ED，三个正方形的边长分别为2、3、5，
∴VB：DE=AB：AD，即VB：5=2：（2+3+5）=1：5，
∴VB=1，
∵CF∥ED，
∴CF：DE=AC：AD，即CF：5=5：10
∴CF=2.5，
∵S梯形VBFC=（BV+CF）•BC=，
∴阴影部分的面积=S正方形BCQW﹣S梯形VBCF=．
故答案为.
21、（2n，1）
【解析】
试题分析：根据图形分别求出n=1、2、3时对应的点A4n+1的坐标，然后根据变化规律写出即可：
由图可知，n=1时，4×1+1=5，点A5（2，1），
n=2时，4×2+1=9，点A9（4，1），
n=3时，4×3+1=13，点A13（6，1），
∴点A4n+1（2n，1）．
22、4.5
【解析】
根据题意可以求得x的值，从而可以求的这组数据的中位数．
【详解】
解：∵数据1、3、x、5、4、6的平均数是4，
∴
解得：x=5，
则这组数据按照从小到大的顺序排列为：1，3，4，5，5，6
则中位数为
故答案为：4.5
本题考查了中位数和平均数的知识，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数；平均数是指在一组数据中所有数据之和再除以数据的个数．
23、
【解析】
本题是把实际问题转化为解直角三角形问题，由题意，已知DA=200，∠CDB=30°，CB：AB=1：0.5，∠CBD=90°，求CB．设AB=x，则CB=2x，由三角函数得：=tan30°，即=，求出x，从求出CB．即求出山的高度．
解：已知山坡AC的坡度i=1：0.5，
∴设AB=x，则CB=2x，又某人在D处测得山顶C的仰角为30°，即，∠CDB=30°，
∴=tan30°，即=，
解得：x=，
∴CB=2x=，
故答案为．
二、解答题（本大题共3个小题，共30分）
24、
【解析】
先去括号，再把除法统一为乘法把分式化简，再把数代入．
【详解】
解：原式
当时，原式.
本题考查分式的混合运算，通分、分解因式、约分是关键．
25、（1）12，4，0.08， 0.04；（2）补图见解析．
【解析】
分析：（1）直接利用已知表格中3＜x≤6范围的频率求出频数a即可，再求出m的值，即可得出b、n的值；
（2）利用（1）中所求补全条形统计图即可．
详解：（1）由题意可得：10÷0.2=50，a=50×0.24=12（人）．
∵m=50-10-12-16-6-2=4，
∴b==0.08，，解得：n=0.04；
故答案为：12，4，0.08， 0.04 ；
（2）如图所示：
．
点睛：本题主要考查了频数分布直方图，正确将条形统计图和表格中数据相联系是解题的关键．
26、 (Ⅰ) 40；25；（Ⅱ）平均数为5.8次；众数为5；中位数为6；(Ⅲ)176名.
【解析】
（Ⅰ）用5次的人数除以5次的人数所占百分比即可得抽查的总人数；求出6次的人数与总人数的比即可得m的值；(Ⅱ)根据平均数、众数和中位数的定义求解即可；(Ⅲ)先求出6次及以上的学生所占的百分比，用320乘以这个百分比即可得答案.
【详解】
（Ⅰ）12÷30%=40（名）；
×100%=25%，
∴m=25，
故答案为40；25
(Ⅱ)平均数为：（6×4+12×5+10×6+8×7+4×8）÷40=5.8(次)
∵这组数据中，5出现了12次，出现次数最多，
∴这组数据的众数为5，
∵将这组数据从小到大排列，其中处于中间的两个数都是6，
∴=6，即中位数为6，
(Ⅲ)6次及以上的学生人数为10+8+4=22（名）
∴×320=176（名）
答：估计该校名九年级男生中该项目良好的人数为176名.
本题考查了条形统计图，扇形统计图，掌握平均数、众数和中位数的定义是解题的关键．
题号
一
二
三
四
五
总分
得分
活动次数x
频数
频率
0＜x≤3
10
0.20
3＜x≤6
a
0.24
6＜x≤9
16
0.32
9＜x≤12
6
0.12
12＜x≤15
b
m
15＜x≤18
2
n