江苏省泰兴市分界镇初级中学2024-2025学年九年级数学第一学期开学学业质量监测模拟试题【含答案】

这是一份江苏省泰兴市分界镇初级中学2024-2025学年九年级数学第一学期开学学业质量监测模拟试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图是根据某班 40 名同学一周的体育锻炼情况绘制的统计图，该班 40 名同学一周参加体育锻炼时间的中位数，众数分别是（ ）
A．10.5，16B．8.5，16C．8.5，8D．9，8
2、（4分）下列分解因式正确的是（ ）
A．－a＋a3=－a(1＋a2)B．2a－4b＋2=2(a－2b)
C．a2－4=(a－2)2D．a2－2a＋1=(a－1)2
3、（4分）若分式的值为零，则x的值是( )
A．2或-2B．2C．-2D．4
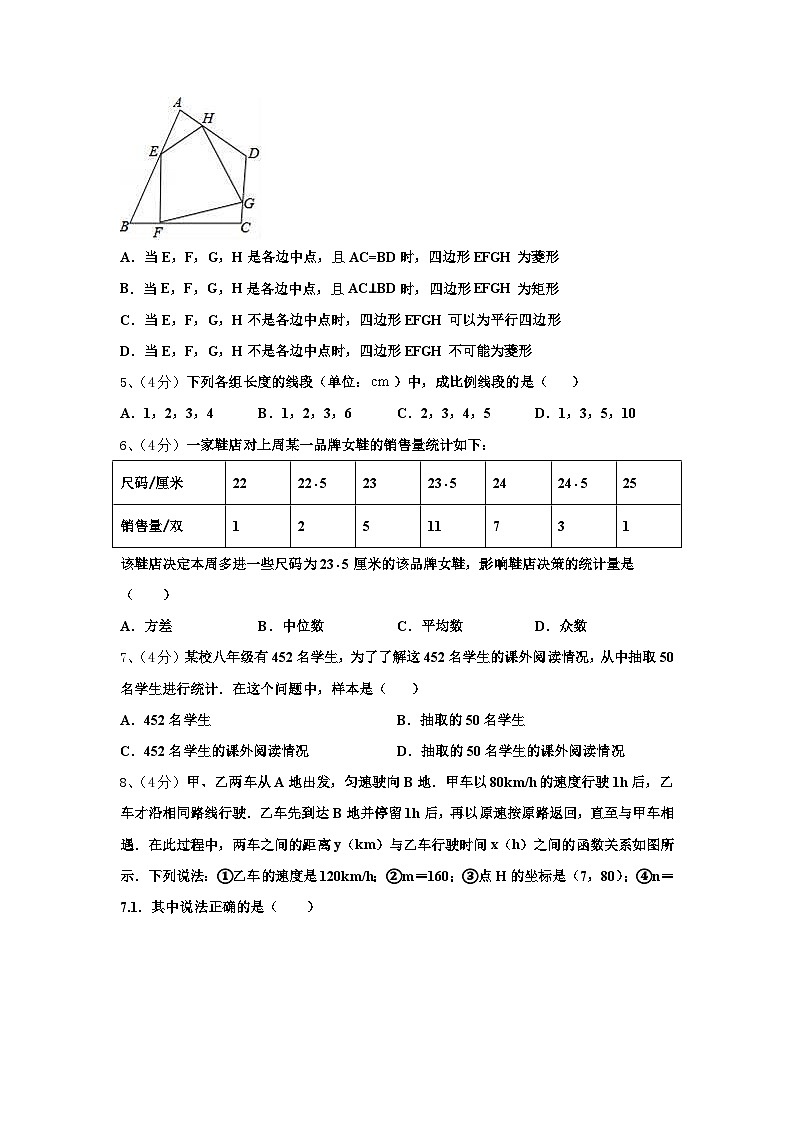
4、（4分）如图，任意四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，对于四边形EFGH的形状，某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ）
A．当E，F，G，H是各边中点，且AC=BD时，四边形EFGH为菱形
B．当E，F，G，H是各边中点，且AC⊥BD时，四边形EFGH为矩形
C．当E，F，G，H不是各边中点时，四边形EFGH可以为平行四边形
D．当E，F，G，H不是各边中点时，四边形EFGH不可能为菱形
5、（4分）下列各组长度的线段（单位：）中，成比例线段的是（ ）
A．1，2，3，4B．1，2，3，6C．2，3，4，5D．1，3，5，10
6、（4分）一家鞋店对上周某一品牌女鞋的销售量统计如下：
该鞋店决定本周多进一些尺码为23.5厘米的该品牌女鞋，影响鞋店决策的统计量是（ ）
A．方差B．中位数C．平均数D．众数
7、（4分）某校八年级有452名学生，为了了解这452名学生的课外阅读情况，从中抽取50名学生进行统计．在这个问题中，样本是（ ）
A．452名学生B．抽取的50名学生
C．452名学生的课外阅读情况D．抽取的50名学生的课外阅读情况
8、（4分）甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.1．其中说法正确的是（ ）
A．①②③B．①②④C．①③④D．①②③④
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）在正方形ABCD中，对角线AC、BD相交于点O．如果AC =，那么正方形ABCD的面积是__________．
10、（4分）分解因式=____________.
11、（4分）如图，正方形的边长为12，点、分别在、上，若，且，则______．
12、（4分）如图，正方形ABCD是由两个小正方形和两个小长方形组成的，根据图形写出一个正确的等式：_________.
13、（4分）如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则点C坐标为______．
三、解答题（本大题共5个小题，共48分）
14、（12分）先化简再求值：，其中．
15、（8分）如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
（1）求证：四边形AODE是矩形；
（2）若AB＝2，AC＝2，求四边形AODE的周长．
16、（8分）计算下列各题：（1） ；（2）.
17、（10分）如图，在平面直角坐标系xOy中，直线y=﹣2x+a与y轴交于点C （0，6），与x轴交于点B．
（1）求这条直线的解析式；
（2）直线AD与（1）中所求的直线相交于点D（﹣1，n），点A的坐标为（﹣3，0）．
①求n的值及直线AD的解析式；
②求△ABD的面积；
③点M是直线y=﹣2x+a上的一点（不与点B重合），且点M的横坐标为m，求△ABM的面积S与m之间的关系式．
18、（10分）如图，在中，，，点在延长线上，点在上，且，延长交于点，连接、．
（1）求证：；
（2）若，则__________．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）两个相似三角形的周长分别为8和6，若一个三角形的面积为36，则另一个三角形的面积为________.
20、（4分）若一组数据1，3，x，4，5，6的平均数是4，则这组数据的众数是_____．
21、（4分）已知P1（x1,y1），P2（x2 ，y2）两点都在反比例函数的图象上，且x1< x2 < 0，则y1 ____ y2.（填“>”或“
【解析】
根据反比例函数的增减性，k=1>0，且自变量x＜0，图象位于第三象限，y随x的增大而减小，从而可得结论．
【详解】
在反比例函数y=中，k=1＞0，
∴该函数在x＜0内y随x的增大而减小．
∵x1＜x1＜0，
∴y1＞y1．
故答案为：＞．
本题考查了反比例函数的性质，解题的关键是得出反比例函数在x＜0内y随x的增大而减小．本题属于基础题，难度不大，解决该题型题目时，根据系数k的取值范围确定函数的图象增减性是关键．
22、1
【解析】
利用因式分解法先求出方程的两个根，再利用勾股定理进行求解即可.
【详解】
方程x2-14x+48=0，即(x-6)(x-8)=0，
则x-6=0或x-8=0，
解得：x1=6，x2=8，
则矩形的对角线长是：=1，
故答案为：1．
本题考查了矩形的性质，勾股定理，解一元二次方程等知识，熟练掌握相关知识是解题的关键.
23、 ．
【解析】
分析：根据勾股定理分别求出直角三角形的斜边长，从而得出一般性的规律．
详解：∵，，，……，．
点睛：本题主要考查的是直角三角形的勾股定理以及规律的发现，属于基础题型．解决这种问题的关键就是得出前面几个三角形的斜边，从而得出一般性的规律．
二、解答题（本大题共3个小题，共30分）
24、（1），；（2）2，2，1，1（答案不唯一）；（3）＝7或＝1．
【解析】
(1)∵，
∴，
∴a＝m2＋3n2，b＝2mn．
故答案为m2＋3n2，2mn．
(2)设m＝1，n＝2，∴a＝m2＋3n2＝1，b＝2mn＝2．
故答案为1，2，1，2(答案不唯一)．
(3)由题意，得a＝m2＋3n2，b＝2mn．
∵2＝2mn，且m、n为正整数，
∴m＝2，n＝1或m＝1，n＝2，
∴a＝22＋3×12＝7，或a＝12＋3×22＝1．
25、（1）详见解析；（2）
【解析】
（1）依据HL判定Rt△ADE≌Rt△ADF，即可得出AE=AF；
（2）判定△DEM≌△DFN，可得S△DEM=S△DFN，进而得到S四边形AMDN=S四边形AEDF，求得S△ADF=AF×DF=2，即可得出结论．
【详解】
（1）∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，
∴DE＝DF，
又∵DE⊥AB于点E，DF⊥AC于点F，
∴∠AED＝∠AFD＝90°，
又∵AD＝AD，
∴Rt△ADE≌Rt△ADF（HL），
∴AE＝AF；
（2）∵∠MDN+∠BAC＝180°，
∴∠AMD+∠AND＝180°，
又∵∠DNF+∠AND＝180°
∴∠EMD＝∠FND，
又∵∠DEM＝∠DFN，DE＝DF，
∴△DEM≌△DFN，
∴S△DEM＝S△DFN，
∴S四边形AMDN＝S四边形AEDF，
∵AD＝6，DF＝2 ，
∴Rt△ADF中，AF＝
∴
∴
本题主要考查了全等三角形的性质和判定、角平分线的性质定理等知识；熟练掌握全等三角形的判定与性质是解决问题的关键．
26、证明见解析
【解析】
根据全等三角形的判定得出△BAE与△CAF全等，进而解答即可．
【详解】
证明：∵∠BAC＝∠EAF，
∴∠BAC﹣∠EAC＝∠EAF﹣∠EAC，
∴∠BAE＝∠CAF，
在△BAE与△CAF中，
，
∴△BAE≌△CAF（SAS）
∴∠AEB＝∠AFC．
本题考查全等三角形的判定和性质，解题的关键是根据全等三角形的判定得出△BAE与△CAF全等．
题号
一
二
三
四
五
总分
得分
尺码/厘米
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1