2024届中考数学二次函数天天练（6）及答案

这是一份2024届中考数学二次函数天天练（6）及答案，共7页。

A.米B.米C.米D.米
2.在平面直角坐标系中，将二次函数的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示（实线部分）.若直线与新函数的图象有3个公共点，则b的值是( )
A.0B.-3C.-4D.-5
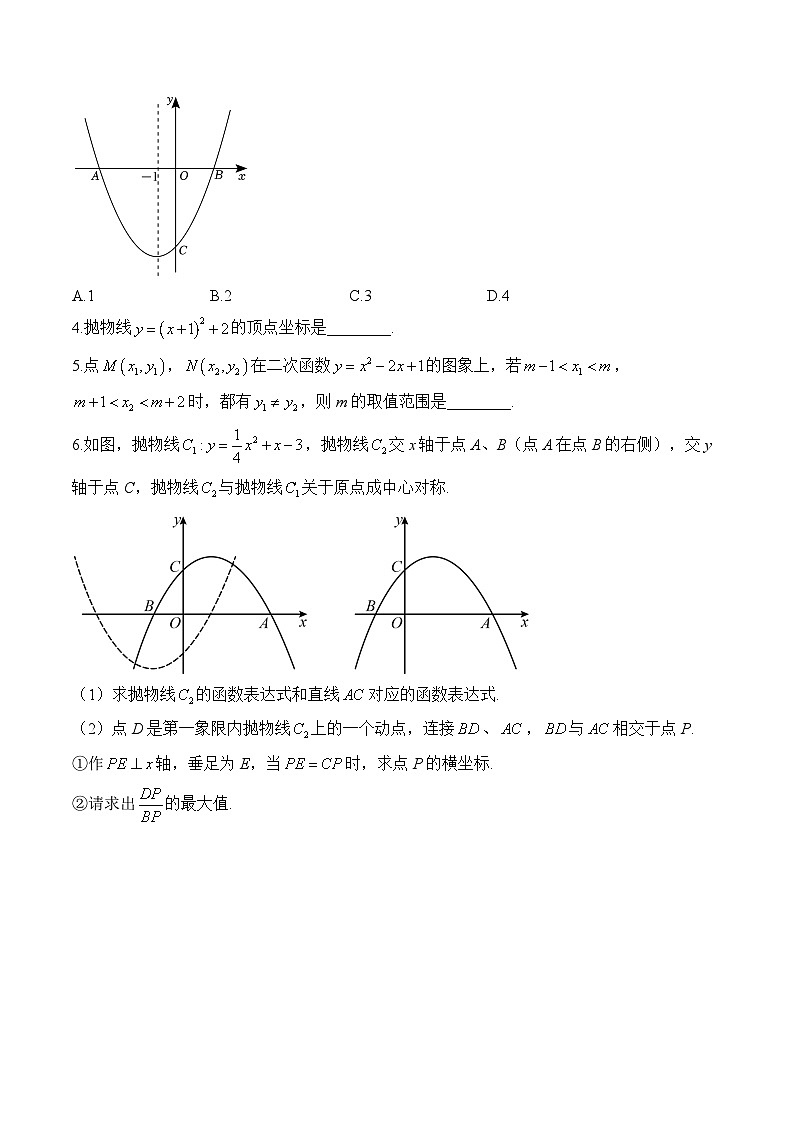
3.如图，抛物线与x轴交于点，B，与x轴交于点c，有下列结论：①；②；③；④点，在抛物线上，当时，，其中，正确结论的个数是( )
A.1B.2C.3D.4
4.抛物线的顶点坐标是________.
5.点，在二次函数的图象上，若，时，都有，则m的取值范围是________.
6.如图，抛物线，抛物线交x轴于点A、B（点A在点B的右侧），交y轴于点C，抛物线与抛物线关于原点成中心对称.
（1）求抛物线的函数表达式和直线对应的函数表达式.
（2）点D是第一象限内抛物线上的一个动点，连接、，与相交于点P.
①作轴，垂足为E，当时，求点P的横坐标.
②请求出的最大值.
答案以及解析
1.答案：C
解析：根据题意得：抛物线过点和，对称轴为直线，
设抛物线解析式为，
把和代入解析式得：，
解得，
抛物线解析式为，
，
函数的最大值为，
球在运动中离地面的最大高度为，
故选：C.
2.答案：C
解析：原二次函数，
顶点，
翻折后点C对应的点为，
当直线与新函数的图象有3个公共点，直线过点D，此时.
故选：C.
3.答案：B
解析：∵对称轴为，
∴，，
∵与轴交于点在负半轴上，
∴，
故，，故①错误；②正确；
∵
∴当时，
∴，故③正确；
∵由图象可得，抛物线对称轴为，开口向上
∴当时，y随x的增大而增大
∵
∴，故④错误；
故选：B.
4.答案：
解析：抛物线可转化为：，
抛物线的顶点坐标是，
故答案为：.
5.答案：或
解析：，，
，
，即，
，
点，不关于对称轴对称，
，的中点在对称轴的左边或右边，
即或，
解得：或，
故答案为：或.
6.答案：（1），
（2）①P的横坐标为
②的最大值为：
解析：（1）抛物线，抛物线与抛物线关于原点成中心对称.
抛物线为：，
，
当，
解得：，，
，；
，
当时，，
，
设为，
，
解得：，
为；
（2）①如图，连接，设，
而，
设直线为，
，
解得：，
直线为，
，
解得：，
，，
，
，
解得：，（不符合题意的根舍去），
，
P的横坐标为；
②作于H，而，
，
，
，
，，
，，
，
，，
当时，
的最大值为：.