

2024--2025学年北师大版九年级上册 数学期中试卷 (A)
展开
这是一份2024--2025学年北师大版九年级上册 数学期中试卷 (A),共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
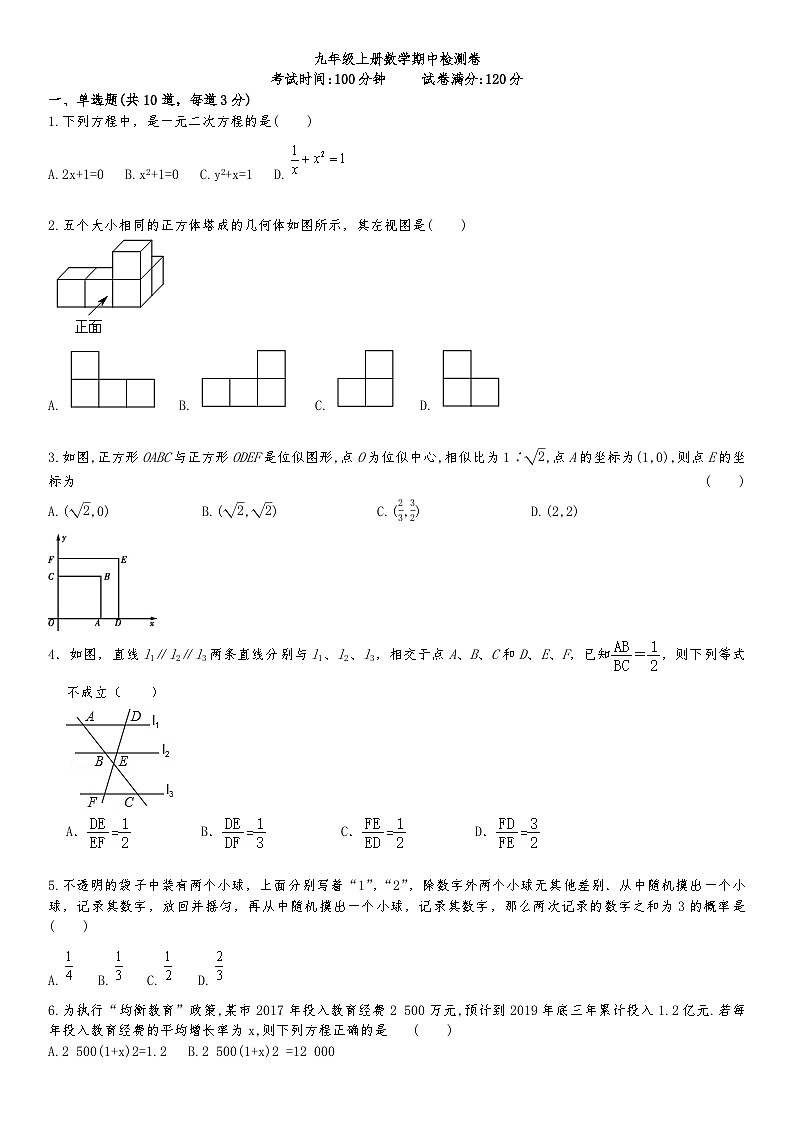
一、单选题(共10道,每道3分)
1.下列方程中,是一元二次方程的是( )
A.2x+1=0 B.x2+1=0 C.y2+x=1 D.
2.五个大小相同的正方体塔成的几何体如图所示,其左视图是( )
A. B. C. D.
3.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶2,点A的坐标为(1,0),则点E的坐标为( )
A.(2,0) B.(2,2) C.(23,32) D.(2,2)
4.如图,直线l1∥l2∥l3两条直线分别与l1、l2、l3,相交于点A、B、C和D、E、F,已知=,则下列等式不成立( )
A.B.C.D.
5.不透明的袋子中装有两个小球,上面分别写着“1”,“2”,除数字外两个小球无其他差别.从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为3的概率是( )
A. B. C. D.
6.为执行“均衡教育”政策,某市2017年投入教育经费2 500万元,预计到2019年底三年累计投入1.2亿元.若每年投入教育经费的平均增长率为x,则下列方程正确的是( )
A.2 500(1+x)2=1.2B.2 500(1+x)2 =12 000
C.2 500+2 500(1+x)+2 500(1+x)2=1.2D.2 500+2 500(1+x)+2 500(1+x)2=12 000
7.关于x的一元二次方程x2+(k-3)x+1-k=0根的情况,下列说法正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根 C.无实数根 D.无法确定
8.如图,在矩形ABCD中,AB=6,BC=8,对角线AC,BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是( )
A.5 B. 32 C. 74 D.154
9.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是( )
A.8 B. C. D.4
10.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0B.4C.6D.8
二、填空题(共5道,每道3分)
11.一元二次方程x2+3x=0的解是____.
12.在一次数学活动课上,老师将全班同学分成5个小组进行摸球试验,试验规则如下:在一个不透明的盒子中装有6个黄球和若干个红球,这些球除颜色外其他都相同,将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,这样连续摸球200次.试验结束后,5个小组分别计算出摸出黄球的频率(如下表所示).由此估计,盒子中红球的个数为 .
如图,在平行四边形ABCD中,点M为边AD上一点,AM=2MD,点E,F分别是BM,CM中点,若EF=6,则AM的长为____.
14.如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=6,BD=8,点P是AC延长线上的一个动点,过点P作PE⊥AD,垂足为点E,过点P作PF⊥DC,交DC的延长线于点F,则PE-PF= .
15.如图,在矩形ABCD中,AB=6,BC=8,对角线AC,BD相交于点O,点P为边AD上一动点,连接OP,以OP为折痕,将△AOP折叠,点A的对应点为点E,线段PE与OD相交于点F.若△PDF为直角三角形,则DP的长为____.
三、解答题(共8道,共计75分)
16.(8分)解下列方程.
(1)x(x-2)-3x2=-1;(2)(x+3)2=(1-2x)2.
17.(8分)小亮与小明做掷骰子(质地均匀的正方体,6个面上的点数分别为1,2,3,4,5,6)的试验.
(1)他们共做了50次试验,试验结果如下:
①填空:试验中,“朝上的点数为1”的频率是 .
②小亮说:“根据试验,出现朝上的点数为1的概率最大.”他的说法正确吗?为什么?
(2)两人约定:每次同时掷两枚骰子,如果两枚骰子的点数之和超过6,则小亮获胜,否则小明获胜.小亮与小明谁获胜的可能性大?试说明理由.
18.(8分)如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:=.
19.(9分)已知:矩形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)当m为何值时,四边形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
20.(10分)某商店以40元/千克的价格新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售价格x(元/千克)之间的函数关系式为y=-2x+240(40≤x≤120).
(1)该商店想在销售成本不超过3 000元的情况下,使销售利润达到2 400元,销售价格应定为多少?
(2)在(1)条件下,该商店为了国庆期间促销,经过两次降价将销售价格定为81元/千克且全部售完,求平均每次降价的百分比.
21.(10分)如图1,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB的中点时,四边形ADEF的形状为 ;
(3)延长图1中的DE到点G,使EG=DE,连接AE,AG,FG,得到图2,若AD=AG,判断四边形AEGF的形状,并说明理由.
图1 图2
22.(10分)如图1,在△ABC中,点D在线段AB上,点E在线段CB的延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB.
(1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,请说明理由;
(2)若将“点D在线段AB上,点E在线段CB的延长线上”改为“点D在线段BA的延长线上,点E在线段BC的延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长.
图1 图2
(10分)如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接BE,点M,N,P分别为DE,BE,BC的中点.
(1)观察猜想
图1中,线段NM,NP的数量关系是 ,∠MNP的大小为 ;
(2)探究证明
把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP,BD,CE,判断△MNP的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请求出△MNP面积的最大值.
参考答案
1答案:B
解题思路:
2答案:C
解题思路:
3.B 【解析】 由正方形的性质得,OA=OC=1,因为正方形OABC与正方形ODEF的相似比为1∶,所以DE=EF=,所以点E的坐标为(,).故选B.
4.【解答】解:∵l1∥l2∥l3,
∴,故A正确
∴,故B正确
∴,故D正确;
故选:C.
5答案:C
6.D 【解析】 由题意得,2018年投入的教育经费为2 500(1+x)万元,2019年投入的教育经费为2 500(1+x)2万元,预计到2019年底,三年累计投入[2 500+2 500(1+x)+2 500(1+x)2]万元,所以2 500+2 500(1+x)+2 500(1+x)2 =12 000.故选D.
7答案:A
解题思路:
8.C 【解析】 在Rt△ABC 中,AB=6,BC=8,∴AC=10,∴AO=AC=5.∵EO⊥AC,∴∠AOE=∠ADC=90°.又∵∠EAO=∠CAD,∴△AEO∽△ACD,∴=,即=,解得AE=,∴DE=8-=.故选C.
9答案:B
解题思路:
10.【解答】解:如图,作点F关于BC的对称点M,连接FM交BC于点N,连接EM,交BC于点H
∵点E,F将对角线AC三等分,且AC=12,
∴EC=8,FC=4=AE,
∵点M与点F关于BC对称
∴CF=CM=4,∠ACB=∠BCM=45°
∴∠ACM=90°
∴EM==4
则在线段BC存在点H到点E和点F的距离之和最小为4<9
在点H右侧,当点P与点C重合时,则PE+PF=12
∴点P在CH上时,4<PE+PF≤12
在点H左侧,当点P与点B重合时,BF==2
∵AB=BC,AE=CF,∠BAE=∠BCF
∴△ABE≌△CBF(SAS)
∴BE=BF=2
∴PE+PF=4
∴点P在BH上时,4<PE+PF≤4
∴在线段BC上点H的左右两边各有一个点P使PE+PF=9,
同理在线段AB,AD,CD上都存在两个点使PE+PF=9.
即共有8个点P满足PE+PF=9,
故选:D.
11答案:x1=0,x2=-3
解题思路:
12.24 【解析】 由题中表格可知,摸出黄球的频率稳定在0.20左右,所以估计摸一次球,摸出黄球的概率为0.2,所以盒子中小球约有6÷0.2=30(个),所以估计红球的个数为30-6=24.
13答案:8
解题思路:
14.4.8 【解析】 延长BC交PE于点G,∵四边形ABCD是菱形,∴AD∥BC,AC⊥BD,且AC与BD互相平分.又∵AC=6,BD=8,∴AB==5,S菱形ABCD=×6×8=24.∵PE⊥AD,∴PE⊥BG,∴EG==4.8,易证△PFC≌△PGC,∴PG=PF,∴PE-PF=PE-PG=EG=4.8.
15答案:1或
解题思路:
16.【解析】 (1)原方程可化为2x2+2x-1=0,
其中a=2,b=2,c=-1,b2-4ac=22-4×2×(-1)=12,
所以x=-2±122×2=-1±32,
即原方程的根为x1=-1+32,x2=-1-32.
(2)移项,得(x+3)2-(1-2x)2=0,
因式分解,得(3x+2)(-x+4)=0.
所以3x+2=0,或-x+4=0,解得x1=-23,x2=4.
17.【解析】 (1)①0.2
②不正确.因为在一次试验中频率并不一定等于概率,只有当试验次数很大时,频率才趋近于概率.
(2)小亮获胜的可能性大,理由如下.
列表如下:
由表格可知,所有可能的结果共有36种,每一种结果出现的可能性相同.
所以P(点数之和超过6)=2136=712,P(点数之和不超过6)=1536=512.
因为>,所以小亮获胜的可能性大.
18.【解答】证明:∵直线DN∥AF,
∴=,=,
∵在△ABC中,AF是BC边上的中线,
∴FB=FC,
∴=.
19.【解答】解:(1)∵四边形ABCD是正方形,
∴AB=AD,
又∵Δ=m2﹣4(﹣)=m2﹣2m+1=(m﹣1)2,(m﹣1)2=0时,
即m=1时,四边形ABCD是正方形,
把m=1代入x2﹣mx+﹣=0,得x2﹣x+=0,
解得:x=,
∴正方形ABCD的边长是;
(2)把AB=2代入x2﹣mx+﹣=0,得4﹣2m+﹣=0,
解得:m=,
把m=代入x2﹣mx+﹣=0,得x2﹣x+1=0,
解得x=2或x=,
∴AD=,
∵四边形ABCD是矩形,
∴矩形ABCD的周长是2×(2+)=5.
20.【解析】 (1)根据题意得,(x-40)(-2x+240)=2 400,
整理得,x2-160x+6 000=0,
解得x1=60,x2=100.
当x=60时,销售价格为60元/千克,销售量为120千克,则销售成本为40×120=4 800(元),超过了3 000元,不合题意,舍去;
当x=100时,销售价格为100元/千克,销售量为40千克,则销售成本为40×40=1 600(元),低于3 000元,符合题意.
答:销售价格应定为100元/千克.
(2)设平均每次降价的百分比是x,
根据题意得,100(1-x)2=81,
解得x1=0.1=10%,x2=1.9(舍去).
答:平均每次降价的百分比是10%.
21.【解析】 (1)∵DE∥AC,∴∠BDE=∠A.
∵∠DEF=∠A,∴∠DEF=∠BDE,∴AD∥EF.
又∵DE∥AC,∴四边形ADEF为平行四边形.
(2)菱形
∵点D为AB的中点,∴AD=12AB,
∵DE∥AC,点D为AB中点,∴DE=12AC.
∵AB=AC,∴AD=DE.
由(1)知四边形ADEF为平行四边形,
∴四边形ADEF为菱形.
(3)四边形AEGF是矩形.理由如下:
由(1)得,四边形ADEF为平行四边形,
∴AF∥DE,AF=DE.
∵EG=DE,∴AF=EG,
∴四边形AEGF是平行四边形.
∵AD=AG,EG=DE,∴AE⊥EG,
∴四边形AEGF是矩形.
22.【解析】 (1)AC=BF.证明如下:
∵∠ADP=∠ACD+∠A,∠ACB=∠ACD+∠BCD,∠ADP=∠ACB,
∴∠BCD=∠A,
又∵∠CBD=∠ABC,∴△CBD∽△ABC,
∴CDAC=BCBA.
∵FE∥AC,∴BCBA=BEBF,
∴CDAC=BEBF.
∵BE=CD,∴AC=BF.
(2)∵∠ABC=90°,∠BAC=60°,
∴∠ADP=∠ACB=30°,
∴∠BCD=60°,∠ACD=60°-30°=30°.
∵PE∥AC,∴∠E=∠ACB=30°,∠CPE=∠ACD=30°,
∴∠E=∠CPE,
∴CP=CE,
又∵BE=CD,∴BC=DP.
∵∠ABC=90°,∠D=30°,
∴BC=12CD,∴DP=12CD,即P为CD的中点.
又∵PF∥AC,∴F是AD的中点,
∴FP是△ADC的中位线,∴FP=12AC.
∵∠ABC=90°,∠ACB=30°,
∴AB=12AC,∴FP=AB=2.
∵DP=CP=BC,CP=CE,
∴BC=CE,即C为BE的中点.
又∵EF∥AC,∴A为FB的中点,
∴AC是△BEF的中位线,
∴EF=2AC=4AB=8,
∴PE=EF-FP=8-2=6.
23答案:(1)NM=NP;∠MNP=60°;
(2)△MNP为等边三角形,理由略;
(3)△MNP面积的最大值为.
解题思路:组别
第1组
第2组
第3组
第4组
第5组
摸出黄球的频率
0.19
0.22
0.20
0.19
0.20
朝上的点数
1
2
3
4
5
6
出现的次数
10
9
6
9
8
8
第2枚骰子掷得的点数
和
第1枚骰子掷得的点数
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
相关试卷
这是一份2024--2025学年人教版七年级数学上册 期中模拟测试卷,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2020—2021学年北师大版九年级上册 数学期中测试卷,共2页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份北师大版2023—2024学年九年级上册数学期中复习试卷(含答案),共23页。









