

北师大版数学九年级上册期中复习试卷03(含答案)
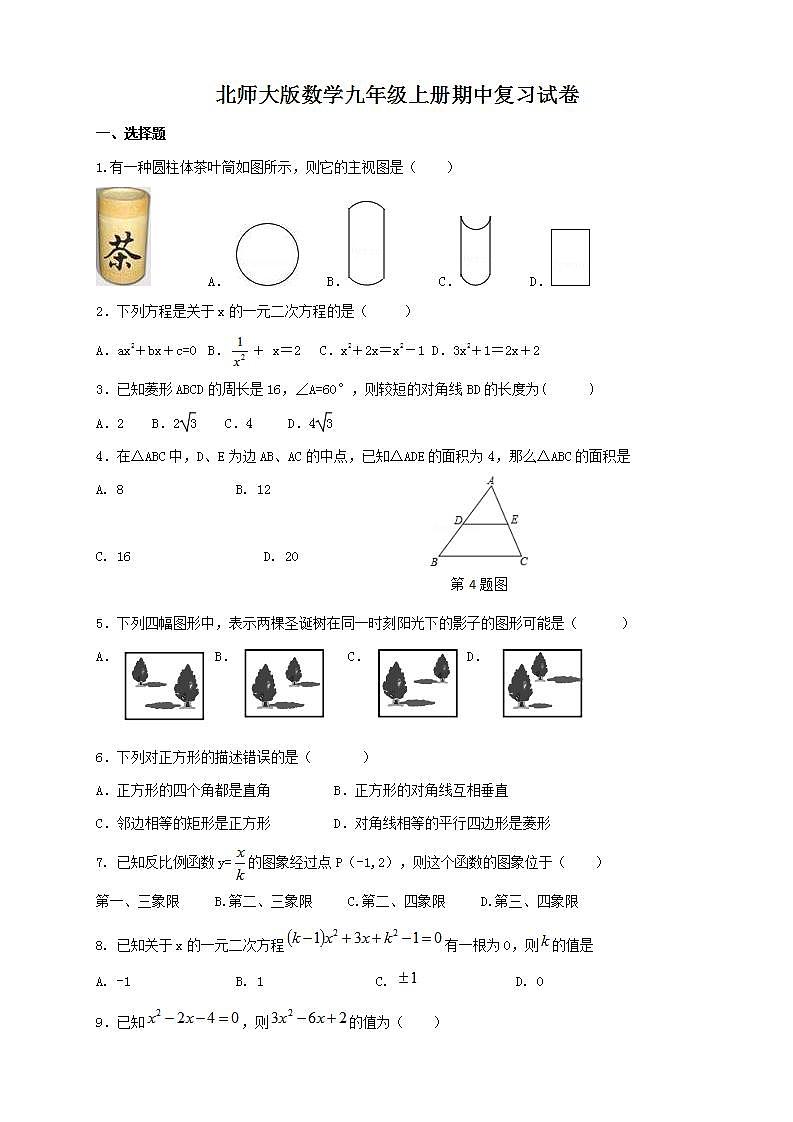
展开1.有一种圆柱体茶叶筒如图所示,则它的主视图是( )
A. B. C. D.
2.下列方程是关于x的一元二次方程的是( )
A.ax2+bx+c=0B. SKIPIF 1 < 0 + x=2C.x2+2x=x2-1D.3x2+1=2x+2
3.已知菱形ABCD的周长是16,∠A=60°,则较短的对角线BD的长度为( )
A.2 B.2 EQ \R(,3) C.4 D.4 EQ \R(,3)
4.在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是
第4题图
A. 8 B. 12
C. 16 D. 20
5.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A. B. C. D.
6.下列对正方形的描述错误的是( )
A.正方形的四个角都是直角 B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形 D.对角线相等的平行四边形是菱形
7. 已知反比例函数y= SKIPIF 1 < 0 的图象经过点P(-1,2),则这个函数的图象位于( )
第一、三象限 B.第二、三象限 C.第二、四象限 D.第三、四象限
8. 已知关于x的一元二次方程 SKIPIF 1 < 0 有一根为0,则 SKIPIF 1 < 0 的值是
A. -1B. 1 C. SKIPIF 1 < 0 D. 0
9.已知 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的值为( )
A.13 B.14 C.11 D.12
10. 如果两点P1(1,y1)和P2(2,y2)都在反比例函数y=- SKIPIF 1 < 0 的图象上,那么( )
A.y2<y1<0 B. y1<y2<0 C. y2>y1>0 D. y1>y2>0
11.如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B、C、D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A、E、D在同一条直线上,若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
A.60m B.40m C.30m D.20m
12.已知粉笔盒里有4支红色粉笔和n支白色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,取出红色粉笔的概率是 SKIPIF 1 < 0 ,则n的值是
A.4 B.6 C.8D.10
13.如图,10×2网格中有一个△ABC,下图中与△ABC相似的三角形的个数有( )
②
①
C
A
B
④
③
A
B
C
D
P
14题图
A.1个 B.2个 C.3个 D.4个
14.如图,在△ABC中,∠ACB=90°,∠ABC=60°,
BD平分∠ABC,P点是BD的中点,若AD=6,
则CP的长为( )
A.3 B.3.5 C.4 D.4.5
15如图,△OAB和△ACD是等边三角形,O、A、C在x轴上,B、D在y= SKIPIF 1 < 0 (x>0)的图象上,则点C的坐标是( )
(﹣1+,0) B.(1+,0)
C.(2,0) D.(2+,0)
二、填空题
16..若 SKIPIF 1 < 0 = SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 的值为_____.
17.如果关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 有两个相等的实数根,那么 SKIPIF 1 < 0 = _____.
18.在平面直角坐标系中,△ABC顶点A的坐标为(2,3),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于1:2,则点A′的坐标__________.
19题图
19.如上图,在矩形ABCD中,AB=9,BC=12,点E是BC的中点,点F是CD边上的任意一点,当ΔAEF的周长最小时,DF=_________。
20已知:多项式x2-kx+1是一个完全平方式,则反比例函数y= SKIPIF 1 < 0 的解析式为________.
21题图
21.如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+,其中正确结论的序号为________________ 。
三、解答题
22.用适当的方法解下列方程:
(1)x(x-2)+x-2=0 (2) SKIPIF 1 < 0
23、(1)一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请你画出从正面、左面看到的这个几何体的形状图.
(2).已知,已知点E是矩形ABCD的边CD上一点,BF⊥AE于点F,求证△ABF∽△EAD.
24.某服装店出售某品牌的棉衣,进价为100元/件,当售价为150元/件时,平均每天可卖30件;为了减少库存迎接“元旦”的到来,商店决定降价销售,增加利润,经调查每件降价5元,则每天可多卖10件,现要想平均每天获利2000元,且让顾客得到实惠,那么每件棉衣应降价多少元?
25.在一个不透明的布袋里装有4个标号为1、2、-3、-4.的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)小凯从布袋里随机取出一个小球,记下数字为x,求x为负数的概率;
(2)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(3)求点P(x,y)在反比例函数y= SKIPIF 1 < 0 图象上的概率.
26.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明
27.如图,点A(3,2)和点M(m,n)都在反比例函数y=k/x(x>0)的图象上。
(1)k的值为______;
(2)当m=4,求直线AM的解析式;
(3)当m>3时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交X轴与点Q,试说明四边形ABPQ是平行四边形。
Q
28.如图.己知四边形ABCD中,AB∥DC,AB=DC,且AB=6cm,BC=8cm,对角线AC=l0cm.
(1)求证:四边形ABCD是矩形;
(2)如图(2),若动点Q从点C出发,在CA边上以每秒5 cm的速度向点A匀速运动,同时动点P从点B出发,在BC边上以每秒4 cm的速度向点C匀速运动,运动时间为t秒(0≤t<2),连接BQ、AP,若AP⊥BQ,求t的值;
(3)如图(3),若点Q在对角线AC上,CQ=4cm,动点P从B点出发,以每秒1cm的速度沿BC运动至点C止.设点P运动了t 秒,请你探索:从运动开始,经过多少时间,以点Q、P、C为顶点的三角形是等腰三角形?请求出所有可能的结果.
图(1)
A
B
C
D
图(2)
A
Q
P
B
C
D
图(3)
A
Q
P
B
C
D
数学答案
一、DDCCB DCABC BBDAC
二、16. 7/4 17. 9 18. (4,6)或(-4,-6)19. 6 20. y=1/x 或y= -3/x
21. = 1 \* GB3 ① = 2 \* GB3 ② = 3 \* GB3 ③
三、22. (1)x= -1或 x= 2 (2)x= -3或x= -5
23(略)
24解:设每件棉衣应降价x元,由题意得到方程
(150-x-100)(30+x/5﹡10)=2000
解得:x1=10(不符合题意舍去)x2=25
答:每件棉衣应降价25元
25解(1)p(x为负)=1/2
(2)
点p的坐标共有12种情况。
(3)有2个坐标在y=2/x上,所以p=2/12=1/6
26(略)
Q
27解:(1)k=6
(2)y=-1/2x+7/2
(3)把M(m,n)代入y=6/x得m=6/n
所以M(6/n,n)
把M,A点坐标代入y=kx+b得
k= -n/3,b=2+n
所以直线AM解析式为y=-n/3x+2+n
所以Q(6/n+3,0)
又因为MP⊥x轴
所以P(6/n,0)
所以PQ=OQ-OP=3
因为AB⊥y轴
图(2)
A
Q
P
B
C
D
N
所以AB‖PQ,AB=3
所以AB=PQ
所以四边形ABPQ是平行四边形。
28(1)(略)
(2)过Q作QN⊥BC于N点CQ=5t,AB=6,BC=8,AB=10,
BP=4t。由△CQN~△CAB得QN=3t,CN=4t。
因为AP⊥BQ,所以△ABP~△BNQ,所以t=0(舍)或t=7/8
(3) = 1 \* GB3 ①QP=QC时t=1.6 = 2 \* GB3 ②CQ=CP时t=4 = 3 \* GB3 ③PQ=PC时t=5.51
2
-3
-4
1
(1,2)
(1,-3)
(1,-4)
2
(2,1)
(2,-3)
(2,-4)
-3
(-3,1)
(-3,2)
(-3,-4)
-4
(-4,1)
(-4,2)
(-4,-3)
苏科版数学九年级上册月考复习试卷03(含答案): 这是一份苏科版数学九年级上册月考复习试卷03(含答案),共12页。试卷主要包含了选择题等内容,欢迎下载使用。
北师大版数学九年级上册期末模拟试卷03(含答案): 这是一份北师大版数学九年级上册期末模拟试卷03(含答案),共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
苏科版数学九年级上册期中复习试卷03(含答案): 这是一份苏科版数学九年级上册期中复习试卷03(含答案),共9页。试卷主要包含了抛物线y=2等内容,欢迎下载使用。













