江苏省无锡市江阴市南闸实验学校2024-2025学年八年级上学期10月质量调研数学试题

这是一份江苏省无锡市江阴市南闸实验学校2024-2025学年八年级上学期10月质量调研数学试题，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共10小题，每小题3分，共30分）
1．下列四个图形中，是轴对称图形的是（ ▲ ）
A． B． C． D．
2. 下列说法中，正确的是（ ▲ ）
A．面积相等的两个图形是全等图形 B．形状相同的两个图形是全等图
C．全等图形的面积相等 D．周长相等的两个图形是全等图形
3．已知一个等腰三角形的两边长分别是 2 和 4 ，则该等腰三角形的周长为（ ▲ ）
A．10 B．8 C．6或12 D． 8或10
4．下列选项所给条件能画出唯一△ABC的是（ ▲ ）
A．AC＝3，AB＝4，BC＝8B．∠A＝50°，∠B＝30°，AB＝2
题5 题7 题8
C．∠C＝90°，AB＝90D．AC＝4，AB＝5，∠B＝60°
如图，小芳做了一个角平分仪ABCD，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整 AB 和 AD，使它们分别落在角的两边上，过点 A、C 画一条射线 AE，AE 就是
∠PRQ 的平分线．此角平分仪的画图原理是（ ▲ ）
A．SSSB．SASC．ASAD．AAS
6．有 A、B、C 三名选手站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在 △ABC 的（ ▲ ）
A．三边中线的交点 B．三条角平分线的交点
C．三边垂直平分线的交点 D．三边上高所在直线的交点
7．如图的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，在网格中与△ABC成轴对称的格点三角形一共有（ ▲ ）
A．2个 B．3个 C．4个 D．5个
8．如图，OD平分 ∠AOB，DE⊥AO 于点 E，DE＝4，点 F 是射线OB上的任意一点，则 DF 的长度不可能是（ ▲ ）
A．3B．4C．5D．6
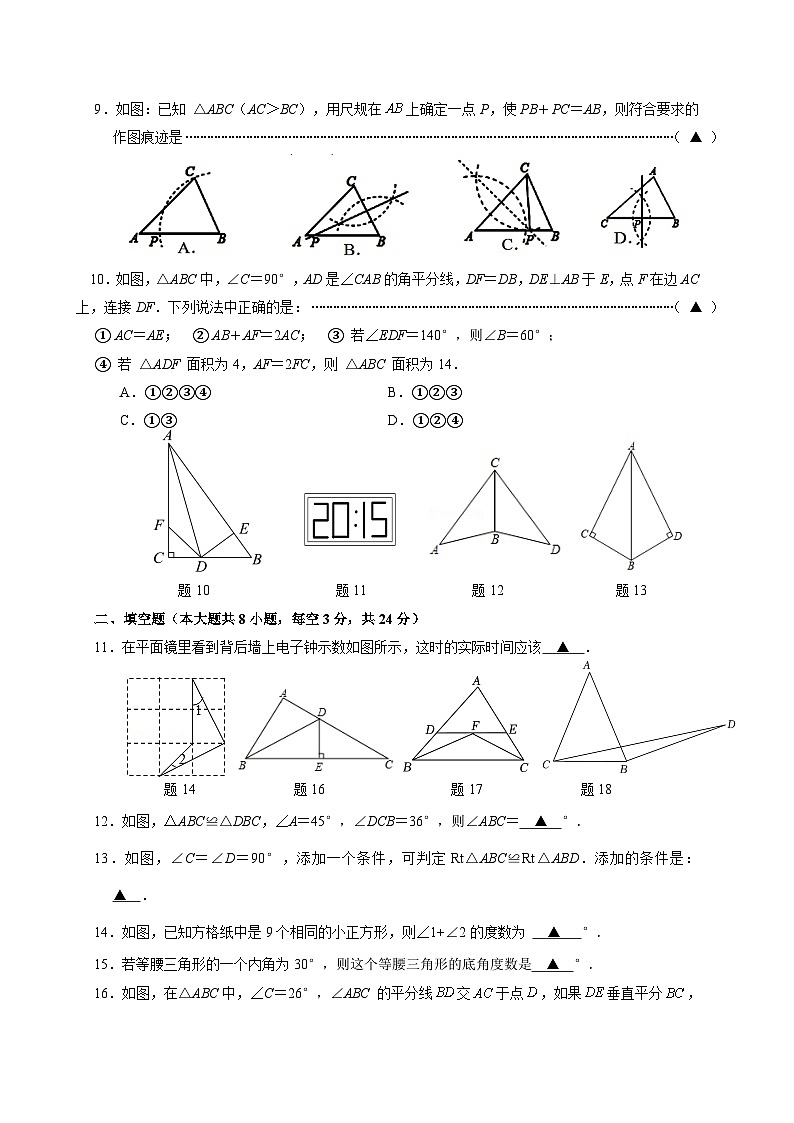
9．如图：已知 △ABC（AC＞BC），用尺规在上确定一点P，使PB＋PC＝AB，则符合要求的作图痕迹是（ ▲ ）

10．如图，△ABC中，∠C＝90°，AD是∠CAB的角平分线，DF＝DB，DE⊥AB于E，点F在边AC上，连接DF．下列说法中正确的是：（ ▲ ）
① AC＝AE； ② AB＋AF＝2AC； ③ 若∠EDF＝140°，则∠B＝60°；
= 4 \* GB3 \* MERGEFORMAT ④ 若 △ADF 面积为4，AF＝2FC，则 △ABC 面积为14．
A．①②③ = 4 \* GB3 \* MERGEFORMAT ④B．①②③
C．①③D．①② = 4 \* GB3 \* MERGEFORMAT ④
题10 题11 题12 题13
二、填空题（本大题共8小题，每空3分，共24分）
11．在平面镜里看到背后墙上电子钟示数如图所示，这时的实际时间应该 ▲ ．
题14 题16 题17 题18
12．如图，△ABC≌△DBC，∠A＝45°，∠DCB＝36°，则∠ABC＝ ▲ °．
13．如图，∠C＝∠D＝90°，添加一个条件，可判定Rt△ABC≌Rt△ABD．添加的条件是： ▲ ．
14．如图，已知方格纸中是9个相同的小正方形，则∠1+∠2的度数为 ▲ °．
15．若等腰三角形的一个内角为30°，则这个等腰三角形的底角度数是 ▲ °．
16．如图，在△ABC中，∠C＝26°，∠ABC 的平分线交于点，如果垂直平分，
则 ∠A＝ ▲ °．
17．如图，在△ABC中，∠B与∠C的平分线交于点F. 过F点作DE∥BC，分别交AB、AC
于D、E．若AB＝3，AC＝2，则△ADE的周长是 ▲ ．
18．如图，AC＝AB＝BD，∠ABD＝90°，BC＝6，则△BCD的面积为 ▲ ．
三、解答题（本大题共7小题，共66分）
19．（本题满分8分） 如图，AC＝AD，BC＝BD，求证：△ABC≌△ABD．
20．（本题满分8分）如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，
AE＝CF，∠D＝∠B，AD∥BC．求证：DF∥EB．
21．（本题满分6分）如图，两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM＝PN，请你通过尺规作图找出这一P点，（不写作法，保留作图痕迹）．
22．（本题满分8分）
（1）如图，在正方形网格上有一个△ABC．作△ABC关于直线MN的对称图形△A1B1C1（不写作法）；
（2）若网格上的最小正方形的边长为1，则△ABC的面积= ．
（3）在直线MN找一点P，使PA＋PC最短.
23.（本题满分12分）如图，在△ABC中，∠ABC＝2∠C，∠BAC的平分线AD交BC于点D，过B作BF⊥AD，垂足为F，延长BF交AC于点E．
（1）求证：△ABE为等腰三角形；
（2）已知BD＝2，AB＝3，求AC的长．
24．（本题满分12分）
某数学兴趣小组开展了一次活动，过程如下：设.∠BAC＝θ°（0°< θ <90°）．现把小棒依次摆放在两射线之间，并使小棒两端分别在射线AB、AC上.
图1 图2
活动一： 如图1所示，从点A1开始，依次向右摆放小棒，使小棒在短点处互相垂直，A1A2为第1根小棒．
数学思考：（1）小棒能无限摆下去吗？答：______. (填“能”或“不能”)
（2）设AA1＝A1A2＝A2A3，θ＝_______°．
活动二：如图2所示，从点A1开始，用等长的小棒依次向右摆放，其中A1A2为第1根小棒，且A1A2＝AA1．
数学思考：（3）若已经摆放了3根小棒，则 θ3＝_______；（用含θ的式子表示）
（4）若只能摆放4根小棒，则 θ 的范围是______________．
25．（本题满分12分）
【阅读理解】
（1）如图3，在△ABC中，AB＝3，AC＝5，D是BC的中点，求BC边上的中线AD的取值范围．小芳在组内经过合作交流，得到了如下的解决方法（也叫“倍长中线法”）：延长AD到E，使DE＝AD，再证明“△ADC≌△EDB”．探究得出AD的取值范围是______________．
【灵活运用】
（2）如图4，△ABC中，∠B＝90°，AB＝2，AC＝7，AD是△ABC的中线，CE⊥BC，AE＝6，且∠ADE＝90°，求CE的长．
【拓展延伸】
（3）如图5，在△ABC中，AD平分∠BAC，且AD交BC于点D，BC的中点为G，过点G作GE平行于AD，交AB于点E，交CA的延长线于点F．若AB＝10，AC＝6，求BE的长．

(第8题)
图3 图4 图5