江西省丰城中学2023-2024学年七年级上学期11月期中考试数学试卷(含解析)

这是一份江西省丰城中学2023-2024学年七年级上学期11月期中考试数学试卷(含解析)，共23页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列计算正确的是( )
A. B.
C. D.
2.借助一副三角尺的拼摆，你能画出度的角．( )
A. B. C. D.
3.下列方程的变形中正确的是( )
A. 由得B. 由得
C. 由得D. 由得
4.关于多项式，下列说法错误的是( )
A. 这个多项式是五次五项式
B. 常数项是
C. 四次项的系数是
D. 按降幂排列为
5.某校七年级班有学生人，其中女生人数比男生人数的多人，则女生的人数为( )
A. B. C. D.
6.如图，数轴上点，，对应的有理数分别为，，，则下列结论中：；；；；，正确的有( )
A. 个B. 个C. 个D. 个
二、填空题：本题共6小题，每小题3分，共18分。
7.单项式次数是______ ．
8.把式子改写成不含括号的形式是______ ．
9.如图是一个运算程序示意图，若第一次输入的值为，则第次输出的结果为______ ．
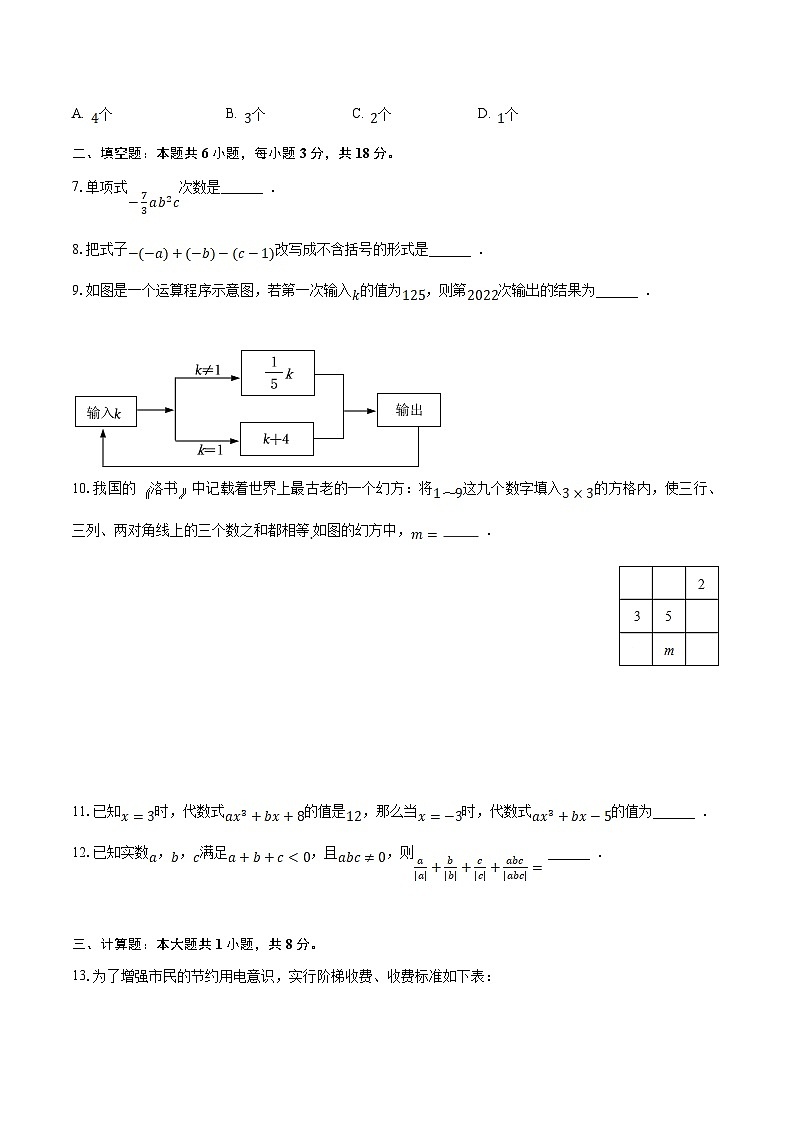
10.我国的洛书中记载着世界上最古老的一个幻方：将这九个数字填入的方格内，使三行、三列、两对角线上的三个数之和都相等如图的幻方中， ．
11.已知时，代数式的值是，那么当时，代数式的值为______ ．
12.已知实数，，满足，且，则 ______ ．
三、计算题：本大题共1小题，共8分。
13.为了增强市民的节约用电意识，实行阶梯收费、收费标准如下表：
若小新家月份用电度，则小新家月份应缴电费______元直接写出结果；
若小新家月份的平均电费为元度，则小新家月份的用电量为多少度？
若小新家月，月共用电度，月和月一共缴电费元，已知月份用电比月份少，求小新家，月各用多少度电电费每个月缴一次？
四、解答题：本题共10小题，共76分。解答应写出文字说明，证明过程或演算步骤。
14.本小题分
计算：
；
．
15.本小题分
解方程：
．
．
16.本小题分
先化简，再求值：
，其中，．
，其中，．
17.本小题分
已知、、在数轴上的位置如图：
______ ， ______ ， ______ 请用“”、“”填空；
化简．
18.本小题分
如图为大连市地铁二号线地图的一部分．某天，小王参加志愿者服务活动，从西安路站出发，到站出站时，本次志愿者服务活动结束，如果规定向东行驶为正，向西为负，当天的乘车站数按先后顺序依次记录如下单位：站：，，，，，，，．
请通过计算说明站是哪一站？小明服务期间距离西安路站最远的站是哪一站？
若相邻两站之间的平均距离为千米，求小王这次做志愿服务期间乘坐地铁行进的总路程约是多少千米？
19.本小题分
仔细观察下列三组数：
第一组：，，，，，
第二组：，，，，，
第三组：，，，，，
根据它们的规律，解答下列问题：
取每组数的第个数，计算它们的和；
取每组数的第个数，它们的和能否是，说明理由．
20.本小题分
在学习整式加减法时，小明同学做了这样一道题目：
化简：



小明发现，化简后含项的系数和为，所以整式的值和的取值无关请根据小明发现的规律，解决下列问题．
已知整式的值与、的取值无关回答下列问题：
直接写出 ______ ， ______ ；
求整式的值；
解关于的方程：．
21.本小题分
已知多项式和，且，．
阅读材料：我们总可以通过添加括号的形式，求出多项式和如：
应用材料：请用类似于阅读材料的方法，求多项式．
小红取，互为倒数的一对数值代入多项式中，恰好得到的值为，求多项式的值．
聪明的小刚发现，只要字母取一个固定的数，无论字母取何数，的值总比的值大，那么小刚所取的的值是多少呢？
22.本小题分
阅读与理解
已知是关于的多项式，记为我们规定：的导出多项式为，记为例如：若，则的导出多项式．
根据以上信息，回答问题：
若，则它的导出多项式______；
设是的导出多项式．
若，求关于的方程的解；
已知是关于的二次多项式，且关于的方程的解为整数，求正整数的值．
23.本小题分
如图，，两点在数轴上对应的数分别为和．
，两点之间的距离为______．
若在数轴上存在一点，使得，求点表示的数．
如图，现有动点，，若点从点出发，以每秒个单位长度的速度沿数轴向右运动，同时点从点出发，以每秒个单位长度的速度沿数轴向左运动，当点到达原点后立即以每秒个单位长度的速度沿数轴向右运动，设运动时间为秒．求：当时的值．
答案和解析
1.【答案】
【解析】解：，即项不合题意，
B.和不是同类项不能合并，即项不合题意，
C.，即项符合题意，
D.，即项不合题意，
故选：．
根据去括号法则和合并同类项法则计算即可求解．
本题考查了整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
2.【答案】
【解析】解：，
由一副三角板拼摆的度数为的整数倍，
故选：．
根据直角三角板中，，与加减组合求解．
本题考查角的计算，解题关键是掌握三角板中三角形的度数与三角板拼摆组成角的度数的关系．
3.【答案】
【解析】解：、由得，故错误；
B、由得，故错误；
C、由得，故错误；
D、由，得，正确．
故选：．
分别对所给的四个方程利用等式性质进行变形，可以找出正确答案．
本题考查解一元一次方程，解一元一次方程的一般步骤是：去分母、去括号、移项、合并同类项、化系数为注意移项要变号．
4.【答案】
【解析】解：、这个多项式是一个五次五项式，原说法正确，故此选项不符合题意；
B、常数项是，原说法正确，故此选项不符合题意；
C、四次项的系数是，原说法错误，故此选项符合题意；
D、按降幂排列为，原说法正确，故此选项不符合题意．
故选：．
根据多项式的相关概念即可求出答案．
本题主要考查了多项式．熟练掌握多项式的相关概念是解题的关键．
5.【答案】
【解析】本题考查了根据数量关系列代数式。解决问题的关键是读懂题意，找到所求的量的等量关系，根据“女生数男生数总人数”进行解答。
【解答】
解：设男生人数为人，则女生的人数为人。
依题意，得：
则
所以
故选A。
6.【答案】
【解析】解：由数轴可得：
，
，故错误；
，，中两负一正，
，故正确；
，，，
，故错误；
，
，故正确；
，故正确；
综上可知，正确的有个．
故选：．
先由数轴得出，再根据有理数的加法法则、有理数的乘除法法则等分别分析，可得答案．
本题考查了数轴在有理数加减乘除法运算中的应用，数形结合，是解题的关键．
7.【答案】
【解析】解：单项式次数是：，
故答案为：．
直接利用单项式的次数的概念：所有字母的指数和即可．
此题考查了单项式，正确把握相关定义是解题的关键．
8.【答案】
【解析】解：；
故答案为：．
根据去括号法则：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反，去掉括号．
本题主要考查了去括号与添括号，熟练掌握去括号法则，符号的确定是解题关键．
9.【答案】
【解析】解：第一次输入，
，
第次输出，
，
第次输出，
，
第次输出，
，
第次输出，
，
第次输出，
按此规律，第次输出，
故答案为：．
根据给定的运算规则，找出输出结果的规律，即可确定．
本题考查了代数式求值，规律型，找出输出结果的规律是解题的关键．
10.【答案】
【解析】
本题考查数的特点和有理数的加法，抓住每行、每列、每条对角线上的三个数之和相等，数的对称性是解题的关键．
根据“每行、每列、每条对角线上的三个数之和相等”解答即可．
【解答】
解：，
根据“每行、每列、每条对角线上的三个数之和相等”，可知三行、三列、两对角线上的三个数之和都等于，
第一列第三个数为：，
第三列第二个数为：，第三个数为：，如图所示：
．
故答案为：．
11.【答案】
【解析】解：时，代数式的值是，
即：，
；
当时：．
故答案为：．
将代入，求出值，将，以及值，代入进行求值即可．
本题考查代数式求值．解题的关键是利用整体思想，代入求值．
12.【答案】或
【解析】解：当，，中有一个负数时，不妨设，
原式；
当，，中有两个负数时，不妨设，，
原式；
当，，都是负数时，即，，，
原式．
故答案为：或．
，，分有一个负数、两个负数和三个负数三种情况分别计算即可得到答案．
本题考查了绝对值，分类讨论的数学思想，掌握正数的绝对值等于它本身，负数的绝对值等于它的相反数是解题的关键．
13.【答案】解：；
设小新家月份用电量为度，
因为当用电量为度时平均电费为，
，
所以小新家月份用电量为第二档，
依题意得：，
解得：，
则小新家月份用电量为度；
设小新家月份用电度，则月份用电度，
第二档电费为元度；
第三档电费为元度，
因为月份用电量小于月份用电量，
所以，，
当时，，
解得：舍去；
当时，，
解得：，
则小新家月份用电量为度，
答：小新家月份用电量为度，月份用电量为度．
【解析】解：根据题意得：
元；
故答案为：；
见答案；
见答案．
判断位于表格中的第二档，列出相应算式，计算即可得到结果；
设小新家月份用电量为度，求出用电量度时的平均电费，判断月份用电量为第二档，根据题意列出方程，求出方程的解即可得到结果；
设小新家月份用电度，则月份用电度，根据表格求出第二档与第三档每度的电费，再由月份用电量小于月份用电量，求出与的范围，分类讨论的范围，列出相应的方程，求出解即可得到结果．
此题考查了有理数的混合运算，以及一元一次方程的应用，弄清题意是解本题的关键．
14.【答案】解：



；



．
【解析】先算乘方和括号内的式子，再算括号外的乘除法，然后算减法即可；
先算乘方，再算乘除法，然后算加减法即可．
本题考查了有理数的混合运算，熟练掌握有理数的运算法则是解题的关键．
15.【答案】解：去分母，得：．
去括号，得：．
移项，得：．
合并同类项，得：．
系数化为，得：．
去分母，得：．
去括号，得：．
移项，得：．
合并同类项，得：．
系数化为，得：．
【解析】去分母、去括号、移项、合并同类项、系数化为即可得；
去分母、去括号、移项、合并同类项、系数化为即可得．
本题考查了解含有分母的一元一次方程，熟练掌握解一元一次方程的步骤和依据是解题的关键．
16.【答案】解：

，
当，时，原式；



，
当，时，原式．
【解析】去括号合并同类项后，再代入求值；
先去括号合并同类项，根据已知结果提取后整体代入．
本题考查了整式的化简求值，掌握去括号法则合并同类项法则是解决本题的关键．
17.【答案】
【解析】解：由图可得，，
，，；
故答案为：，，；
，，，
．
根据、、在数轴上的位置得到，进而求解即可；
根据，，，利用绝对值的性质化简，然后去括号合并求解即可．
本题主要考查的是有理数的大小比较，整式的加减运算，绝对值的化简，根据数轴上各点的位置判断出、、的符号及其大小是解答此题的关键．
18.【答案】解：，东行驶为正，向西为负，
站在西安路站向西两站即辽师大站；
，，，，，，，
的绝对值最大，可知小王服务期间距离西安路站最远在西安路站西侧站，即机场站；
，
小王这次做志愿服务期间乘坐地铁行进站．
相邻两站之间的平均距离为千米，
千米．
答：小王这次做志愿服务期间乘坐地铁行进的总路程约是千米．
【解析】通过计算各数据的代数和，依据题意可得站的站名；通过依次计算每相邻两站的代数和，找出绝对值最大的数即为距离西安路站最远的站；
计算各个数据的绝对值的和即可得到行走的总站数，再乘以即可得出结论．
本题主要考查了有理数的混合运算，绝对值的意义，正数和负数，准确理解数据的实际意义是解题的关键．
19.【答案】解：第一组第个数为：，则第个数为：，
则第二组第个数为：，
第三组第个数为：，
故；
不能，理由如下：
设第一组的第个数是，则第二组的第个数为：，第三组第个数为，


，
所以取每组数的第个数，它们的和是．
【解析】不难看出第一组的第个数为：，第二组的数是第一组相应的数减去，第三组的数是第二组相应的数乘以，据此写出第个数再相加即可；
可设第一组的第个数是，则表示出第二组，第三组相应的数再相加运算即可判断．
本题主要考查数字的变化规律，解答的关键是由所给的数字总结出存在的规律．
20.【答案】
【解析】解：原式
，
原式的值与、的取值无关，
，，
解得：，，
故答案为：；；
当，时，
；
由题意可得方程为，
去分母得：，
去括号得：，
移项，合并同类项得：．
将原式去括号，合并同类项后根据题意即可求得，的值；
将，的值代入中计算即可；
将，的值代入方程中解方程即可．
本题考查整式的加减及解一元一次方程，结合已知条件求得，的值是解题的关键．
21.【答案】解：


，
；
根据题意知，，
，
解得，
，
则


；




，
由题意知，且与字母无关，
，即．
【解析】计算后可得多项式；
由，知，据此求得的值，继而得出的值，再代入计算即可；
先计算得出，根据且与字母无关知，据此可得答案．
本题主要考查整式的加减，几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接；然后去括号、合并同类项．
22.【答案】解：，
因为，
所以它的导出多项式，
因为，
所以，
所以，
所以关于的方程的解为：；
因为，
所以它的导出多项式，
因为，
所以，
所以，
因为关于的方程的解为整数，
所以，
所以，
所以的值为：，，，，
所以的值为：，，，，，，，，
所以正整数的值为：，，，
又因为，
所以，
所以正整数的值为：，，
【解析】
本题考查了新定义，一元一次方程的解，根据题目的已知理解，是解题的关键．
利用题目已知的规定：的导出多项式为，记为，即可解答；
根据题目已知的规定，求出导出的多项式，进行计算即可；
根据题目已知的规定，求出导出的多项式，再根据关于的方程的解为整数，进行计算即可．
【解答】
解：因为，
所以它的导出多项式，
故答案为：，
见答案．
23.【答案】
【解析】解：，两点在数轴上对应的数分别为和，
，两点之间的距离是：，
故答案为：；
设点表示的数为，
当点在线段之间时，
，
，
解得：；
当点在点的左侧时，
，
，
解得：，
综上所述：点表示的数为或；
当时，点表示的数为：，点表示的数为：，
由得：，
解得：或，符合题意；
当时，点表示的数为：，点表示的数为：，
由得：，
解得：或不符合题意，舍去，
综上所述，的值为：或或．
结合，两点在数轴上的位置进行求解即可；
可分两种情况：当点在线段之间时；当点在点的左侧时，结合数轴进行求解即可；
分两种情况：当时；当时，分别表示出点，，结合条件进行求解即可．
本题主要考查一元一次方程的应用，数轴，解答的关键是分类讨论点所在的位置及的值．
每月用电量
收费
第一档
不超过度的部分
电费元度
第二档
度以上至度的部分
每度比上一档提价元
第三档
度以上的部分
每度比上一档提价元