内蒙古通辽市科左中旗2024-2025学年 八年级上学期月考数学试卷

这是一份内蒙古通辽市科左中旗2024-2025学年 八年级上学期月考数学试卷，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
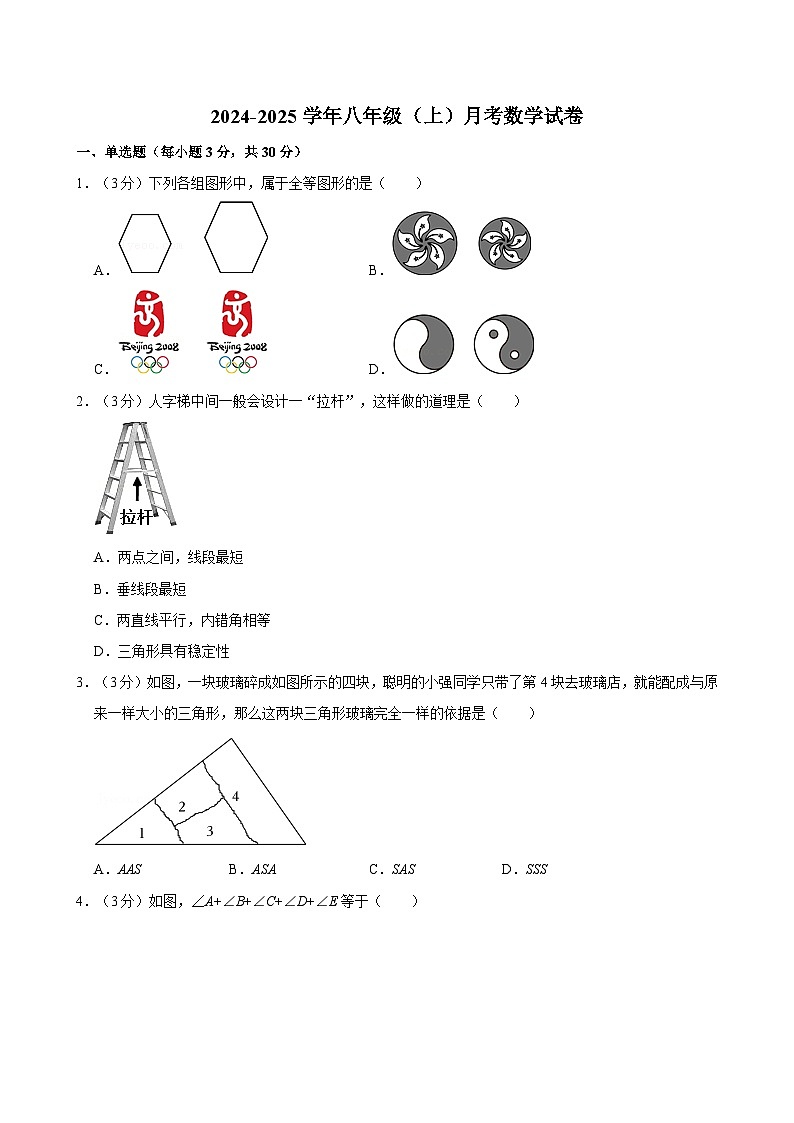
1．（3分）下列各组图形中，属于全等图形的是（ ）
A．B．
C．D．
2．（3分）人字梯中间一般会设计一“拉杆”，这样做的道理是（ ）
A．两点之间，线段最短
B．垂线段最短
C．两直线平行，内错角相等
D．三角形具有稳定性
3．（3分）如图，一块玻璃碎成如图所示的四块，聪明的小强同学只带了第4块去玻璃店，就能配成与原来一样大小的三角形，那么这两块三角形玻璃完全一样的依据是（ ）
A．AASB．ASAC．SASD．SSS
4．（3分）如图，∠A+∠B+∠C+∠D+∠E等于（ ）
A．90°B．120°C．180°D．360°
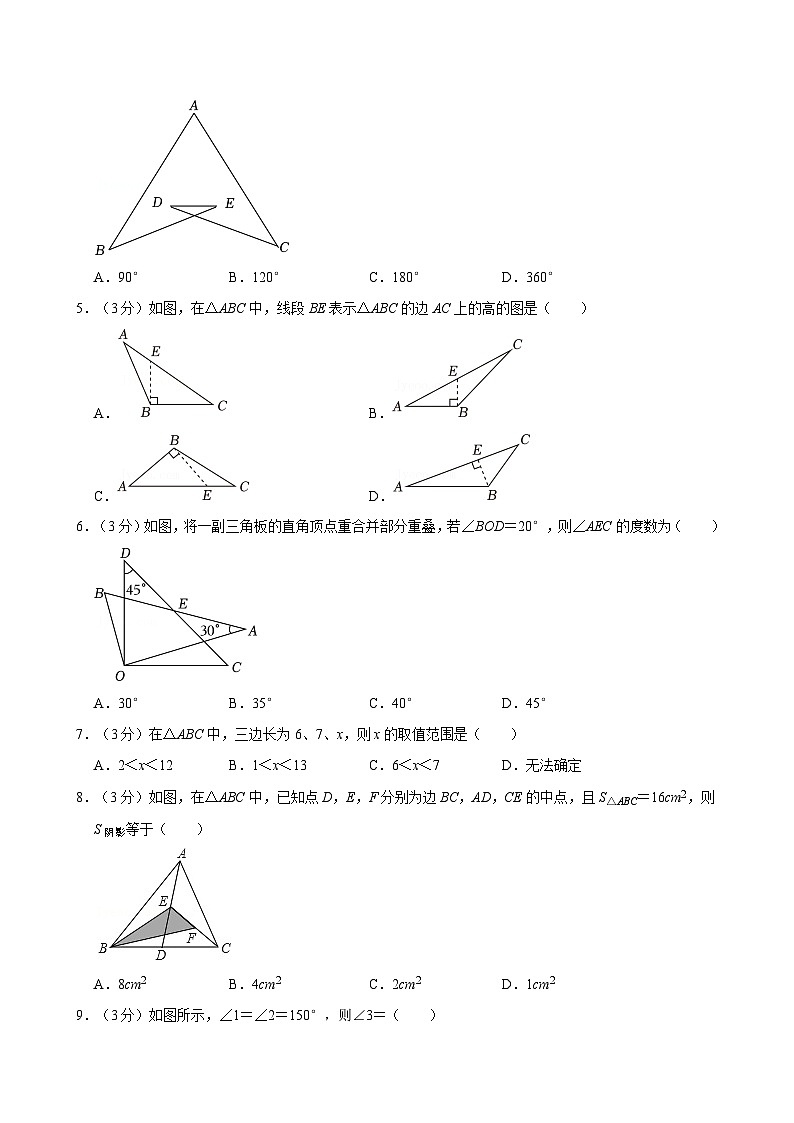
5．（3分）如图，在△ABC中，线段BE表示△ABC的边AC上的高的图是（ ）
A．B．
C．D．
6．（3分）如图，将一副三角板的直角顶点重合并部分重叠，若∠BOD＝20°，则∠AEC的度数为（ ）
A．30°B．35°C．40°D．45°
7．（3分）在△ABC中，三边长为6、7、x，则x的取值范围是（ ）
A．2＜x＜12B．1＜x＜13C．6＜x＜7D．无法确定
8．（3分）如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC＝16cm2，则S阴影等于（ ）
A．8cm2B．4cm2C．2cm2D．1cm2
9．（3分）如图所示，∠1＝∠2＝150°，则∠3＝（ ）
A．30°B．150°C．120°D．60°
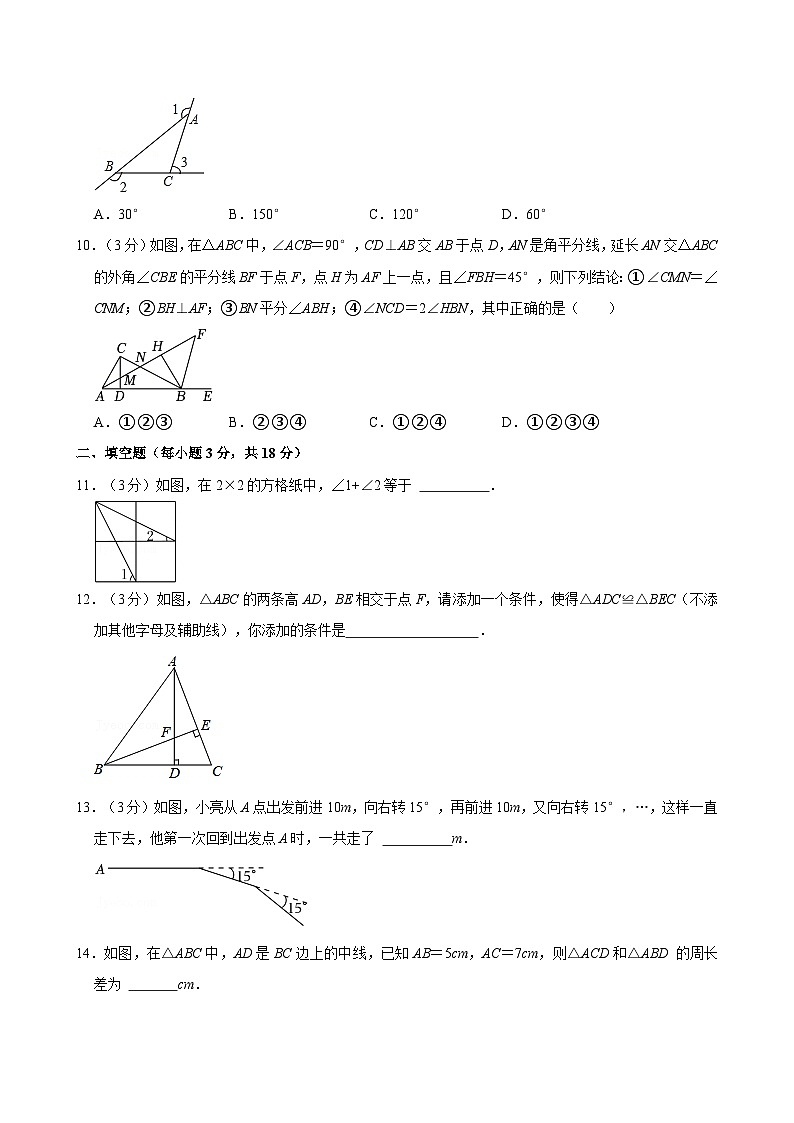
10．（3分）如图，在△ABC中，∠ACB＝90°，CD⊥AB交AB于点D，AN是角平分线，延长AN交△ABC的外角∠CBE的平分线BF于点F，点H为AF上一点，且∠FBH＝45°，则下列结论：①∠CMN＝∠CNM；②BH⊥AF；③BN平分∠ABH；④∠NCD＝2∠HBN，其中正确的是（ ）
A．①②③B．②③④C．①②④D．①②③④
二、填空题（每小题3分，共18分）
11．（3分）如图，在2×2的方格纸中，∠1+∠2等于 ．
12．（3分）如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是 ．
13．（3分）如图，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°，…，这样一直走下去，他第一次回到出发点A时，一共走了 m．
14．如图，在△ABC中，AD是BC边上的中线，已知AB＝5cm，AC＝7cm，则△ACD和△ABD 的周长差为 cm．
15.小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第 块．
16．（3分）如图，AB＝5cm，AC＝BD＝3cm．∠CAB＝∠DBA，点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．设运动时间为t（s），则当点Q的运动速度为 cm/s时，△ACP与△BPQ有可能全等．
三、解答题
17．（6分)已知一个多边形的内角和与外角和的和为1080°，且这个多边形的各个内角都相等．求这个多边形的每个外角度数．
18．（6分）已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，
且∠1＝∠A．若∠BFE＝110°，∠1＝60°，求∠B的度数．
19．（7分）如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC．求证：△ABC≌△ADE．
20．（7分）在直角三角形ABC中，∠ACB＝90°，CD是AB边上的高，AB＝10cm，BC＝8cm，AC＝6cm
（1）求△ABC的面积；
（2）求CD的长；
（3）若△ABC的边AC上的中线是BE，求出△ABE的面积．
21．（8分）已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD．
（1）求证：∠E＝∠F；
（2）若∠A＝40°，∠D＝80°，求∠E的度数．
22．（8分）如图，在四边形ABCD中，点E为对角线BD上一点，∠A＝∠BEC，AD∥BC，且AD＝BE．
（1）证明：△ABD≌△ECB；
（2）若BC＝15，AD＝6，请求出DE的长度．
23．（10分）如图①，在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥MN于点M，BN⊥MN于点N．
（1）求证：MN＝AM+BN；
（2）如图②，若过点C作直线MN与线段AB相交，AM⊥MN于点M，BN⊥MN于点N（AM＞BN），（1）中的结论是否仍然成立？若不成立，请写出正确的结论，并说明理由．
2024-2025学年八年级（上）月考数学试卷
参考答案与试题解析
一、选择题（每小题3分，共30分）
1．（3分）下列各组图形中，属于全等图形的是（ ）
A．B．
C．D．
【分析】能够完全重合的两个图形叫做全等形，由此即可判断．
【解答】解：A、B、两个图形的大小不相同，不能够完全重合，不是全等图形，故A、B不符合题意；
C、两个图形能够完全重合，是全等图形，故C符合题意；
D、两个图形的形状不相同，不能够完全重合，不是全等图形，故D不符合题意；
故选：C．
【点评】本题考查全等图形，关键是掌握全等图形的定义．
2．（3分）人字梯中间一般会设计一“拉杆”，这样做的道理是（ ）
A．两点之间，线段最短
B．垂线段最短
C．两直线平行，内错角相等
D．三角形具有稳定性
【分析】根据三角形的稳定性解答即可．
【解答】解：人字梯中间一般会设计一“拉杆”，是为了形成三角形，利用三角形具有稳定性来增加其稳定性，
故选：D．
【点评】此题考查了三角形的性质，关键是根据三角形的稳定性解答．
3．（3分）如图，一块玻璃碎成如图所示的四块，聪明的小强同学只带了第4块去玻璃店，就能配成与原来一样大小的三角形，那么这两块三角形玻璃完全一样的依据是（ ）
A．AASB．ASAC．SASD．SSS
【分析】根据“配成与原来一样大小的三角形”，分析第4块玻璃碎与原来的三角形存在哪些角、哪些边相等，即可作答．
【解答】解：依题意，聪明的小强同学只带了第4块去玻璃店，
∴第4块玻璃碎与原来的三角形存在两个角、夹边相等，
那么这两块三角形玻璃完全一样的依据是ASA，
故选：B．
【点评】本题考查了全等三角形的应用，三角形的稳定性，解答本题的关键是熟练掌握全等三角形的判定定理．
4．（3分）如图，∠A+∠B+∠C+∠D+∠E等于（ ）
A．90°B．120°C．180°D．360°
【分析】根据三角形内角和定理以及对顶角相等可得答案．
【解答】解：如图，连接BC，
∵∠D+∠E+∠EFD＝180°，∠FBC+∠FCB+∠BFC＝180°，∠DFE＝∠BFC，
∴∠D+∠E＝∠FBC+∠FCB，
∴∠A+∠ABE+∠ACD+∠D+∠E
＝∠A+∠ABE+∠ACD+∠FBC+∠FCB
＝∠A+∠ABC+∠ACB
＝180°，
故选：C．
【点评】本题考查三角形内角和定理，掌握三角形内角和是180°是正确解答的前提．
5．（3分）如图，在△ABC中，线段BE表示△ABC的边AC上的高的图是（ ）
A．B．
C．D．
【分析】根据三角形高的定义判断即可．
【解答】解：过点B作AC的垂线，且垂足在直线AC上，
所以正确画出AC边上的高的是D选项，
故选：D．
【点评】本题主要考查了三角形高线的定义，熟练掌握从三角形的一个顶点向对边所在直线作垂线，顶点与垂足间的线段叫做三角形的高是解题的关键．
6．（3分）如图，将一副三角板的直角顶点重合并部分重叠，若∠BOD＝20°，则∠AEC的度数为（ ）
A．30°B．35°C．40°D．45°
【分析】根据三角形内角和定理求出∠B的度数，进而根据三角形外角的性质求出∠AFO的度数，再由三角形外角的性质求出∠DEF的度数，最后根据对顶角相等即可得到答案．
【解答】解：如图，
由题意得，∠B＝180°﹣30°﹣90°＝60°，
∵∠BOD＝20°，
∴∠AFO＝∠BOD+∠B＝80°，
∴∠DEF＝∠AFO﹣∠D＝35°，
∴∠AEC＝∠DEB＝35°，
故选：B．
【点评】本题主要考查了三角形内角和定理，三角形外角的性质，熟练掌握各知识点是解题的关键．
7．（3分）在△ABC中，三边长为6、7、x，则x的取值范围是（ ）
A．2＜x＜12B．1＜x＜13C．6＜x＜7D．无法确定
【分析】根据三角形的三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边可得7﹣6＜x＜7+6，再解即可．
【解答】解：由题意得：7﹣6＜x＜7+6，
解得：1＜x＜13，
故选：B．
【点评】此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
8．（3分）如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC＝16cm2，则S阴影等于（ ）
A．8cm2B．4cm2C．2cm2D．1cm2
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答．
【解答】解：∵点E是AD的中点，
∴S△DBE＝S△ABD，S△DCE＝S△ADC，
∴S△BCE＝S△ABC＝×16＝8（cm2），
∵点F是CE的中点，
∴S△BEF＝S△BCE＝×8＝4（cm2）．
故选：B．
【点评】本题考查了三角形的面积，主要利用了三角形的中线把三角形分成两个面积相等的三角形，原理为等底同高的三角形的面积相等．
9．（3分）如图所示，∠1＝∠2＝150°，则∠3＝（ ）
A．30°B．150°C．120°D．60°
【分析】由∠1，∠2的度数，利用邻补角互补可求出∠ABC，∠BAC的度数，再利用三角形的外角性质即可求出∠3的度数．
【解答】解：∵∠1＝∠2＝150°，
∴∠ABC＝∠BAC＝180°﹣150°＝30°，
∴∠3＝∠ABC+∠BAC＝60°．
故选：D．
【点评】本题考查了三角形的外角性质以及邻补角，牢记“三角形的一个外角等于和它不相邻的两个内角的和”是解题的关键．
10．（3分）如图，在△ABC中，∠ACB＝90°，CD⊥AB交AB于点D，AN是角平分线，延长AN交△ABC的外角∠CBE的平分线BF于点F，点H为AF上一点，且∠FBH＝45°，则下列结论：①∠CMN＝∠CNM；②BH⊥AF；③BN平分∠ABH；④∠NCD＝2∠HBN，其中正确的是（ ）
A．①②③B．②③④C．①②④D．①②③④
【分析】①先由∠ACB＝90°，CD⊥AB得∠CAN+∠CNM＝90°，∠DAN+∠AMD＝90°，根据角平分线的定义及对顶角的性质得∠CAN＝∠DAN，∠AMD＝∠CMN，据此可对结论①进行判断；
②利用三角形外角性质及角平分线的定义可得出∠CBF＝45°+∠CAN，再证∠CAN+∠ACB＝∠CBF+∠F，据此可得∠F＝45°，然后根据∠FBH＝45°可对结论②进行判断；
③假设BN平分∠ABH，则∠HBN＝∠ABN，然后证∠CAN＝∠DAN＝∠HBN＝∠ABN，由此可求出∠ABN＝30°，然而根据已知条件无法判定∠ABN＝30°，因此假设BN平分∠ABH是错误的，故结论③得到判定；
④由结论①正确得∠CMN＝∠CNM，再由∠CMN+∠CNM+∠DCN＝180°得2∠CNM+∠DCN＝180°，由结论②正确得∠BHN＝90°，则∠HNB＝90°﹣∠HBN，再由∠HNB＝∠CNM可得出2（90°﹣∠HBN）+∠DCN＝180°，据此可对结论④进行判断，综上所述即可得出答案．
【解答】解：①∵∠ACB＝90°，CD⊥AB，
∴∠CAN+∠CNM＝90°，∠DAN+∠AMD＝90°，
∵AN平分∠ACB，
∴∠CAN＝∠DAN，∠CAB＝2∠CAN，
∴∠CNM＝∠AMD
又∵∠AMD＝∠CMN，
∴∠CMN＝∠CNM，
故结论①正确；
②∵∠ACB＝90°，∠CAB＝2∠CAN，
∴∠CBE＝∠ACB+∠CAB＝90°+2∠CAN，
∵BE是∠CBE的平分线，
∴∠CBF＝∠CBE＝45°+∠CAN，
∵∠CAN+∠ACB+∠CNA＝180°，∠CBF+∠F+∠BNF＝180°，∠CNA＝∠BNF，
∴∠CAN+∠ACB＝∠CBF+∠F，
即：∠CAN+90°＝45°+∠CAN+∠F，
∴∠F＝45°，
∵∠FBH＝45°，
∴∠BHF＝180°﹣（∠F+∠FBH）＝90°，
即：BH⊥AF，
故结论②正确；
③假设BN平分∠ABH，则∠HBN＝∠ABN，
由结论②正确得：BH⊥AF，则∠BHN＝90°，
∴∠BNH+∠HBN＝90°
∵∠ACB＝90°，
∴∠CNA+∠CAN＝90°，
∵∠BNH＝∠CNA，
∴∠HBN＝∠CAN，
∵N平分∠ACB，∠HBN＝∠ABN，
∴∠CAN＝∠DAN＝∠HBN＝∠ABN，
即：∠CAB＝2∠ABN，
∵∠CAB+∠ABN＝90°，
∠ABN＝30°，
根据已知条件无法判定∠ABN＝30°，因此假设BN平分∠ABH是错误的．
故结论③不正确；
④由结论①正确得：∠CMN＝∠CNM，
∵∠CMN+∠CNM+∠DCN＝180°，即：2∠CNM+∠DCN＝180°，
由结论②正确得：BH⊥AF，则∠BHN＝90°，
∵∠HNB＝90°﹣∠HBN，
∵∠HNB＝∠CNM，
∴∠CNM＝90°﹣∠HBN，
∴2（90°﹣∠HBN）+∠DCN＝180°，
∴∠NCD＝2∠HBN．
故结论④正确．
综上所述：正确的结论是①②④．
故选：C．
【点评】此题主要考查了角平分线的定义，三角形的内角和定理，直角三角形的性质，熟练掌握角平分线的定义，理解直角三角形的两个锐角互余，灵活运用三角形的内角和进行角度计算是解答此题的关键．
二、填空题（每小题3分，共18分）
11．（3分）如图，在2×2的方格纸中，∠1+∠2等于 90° ．
【分析】标注字母，然后利用“边角边”求出△ABC和△DEA全等，根据全等三角形对应角相等可得∠2＝∠3，再根据直角三角形两锐角互余求解．
【解答】解：如图，在△ABC和△DEA中，
，
∴△ABC≌△DEA（SAS），
∴∠2＝∠3，
在Rt△ABC中，∠1+∠3＝90°，
∴∠1+∠2＝90°，
故答案为：90°．
【点评】本题考查了全等图形，主要利用了网格结构以及全等三角形的判定与性质，准确识图并确定出全等三角形是解题的关键．
12．（3分）如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是 AC＝BC（答案不唯一） ．
【分析】添加AC＝BC，根据三角形高的定义可得∠ADC＝∠BEC＝90°，再添加AC＝BC可利用AAS判定△ADC≌△BEC．
【解答】解：添加AC＝BC（答案不唯一），
∵△ABC的两条高AD，BE，
∴∠ADC＝∠BEC＝90°，
在△ADC和△BEC中，
∴△ADC≌△BEC（AAS），
故答案为：AC＝BC（答案不唯一）．
【点评】此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
13．（3分）如图，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°，…，这样一直走下去，他第一次回到出发点A时，一共走了 240 m．
【分析】由题意可知小亮所走的路线为正多边形，根据多边形的外角和定理即可求出答案．
【解答】解：∵小亮从A点出发最后回到出发点A时正好走了一个正多边形，
∴根据外角和定理可知正多边形的边数为n＝360°÷15°＝24，
则一共走了24×10＝240（米）．
故答案为：240．
【点评】本题主要考查了多边形的外角和定理，掌握任何一个多边形的外角和都是360°是解题的关键．
14.如图，在△ABC中，AD是BC边上的中线，已知AB＝5cm，AC＝7cm，则△ACD和△ABD 的周长差为 2 cm．
【分析】根据三角形的中线的定义得到BD＝DC，再根据三角形周长公式计算即可．
【解答】解：∵AD是BC边上的中线，
∴BD＝DC，
∴△ACD的周长﹣△ABD 的周长＝（AC+AD+DC）﹣（AB+AD+BD）＝AC﹣AB＝7﹣5＝2（cm），
故答案为：2．
【点评】本题考查的是三角形的中线，三角形一边的中点与此边所对顶点的连线叫做三角形的中线．
15.小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第 4 块．
【分析】本题应先假定选择哪块，再对应三角形全等判定的条件进行验证即可得到结论．
【解答】解：1、2、3块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，
只有第4块有完整的两角及夹边，符合ASA，满足三角形全等的条件，是符合题意的，
故答案为：4．
【点评】本题主要考查三角形全等的判定，解决问题的关键的关键是掌握判定两个三角形全等的一般方法：SSS、SAS、ASA、AAS、HL．
16．（3分）如图，AB＝5cm，AC＝BD＝3cm．∠CAB＝∠DBA，点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．设运动时间为t（s），则当点Q的运动速度为 1或 cm/s时，△ACP与△BPQ有可能全等．
【分析】根据题意可得：AP＝t cm，则BP＝（5﹣t）cm，然后根据已知∠CAB＝∠DBA，分两种情况：当AC＝BP＝3cm，AP＝BQ＝t cm时；当AC＝BQ＝3cm，AP＝BP时，分别进行计算即可解答．
【解答】解：由题意得：
AP＝t cm，
∵AB＝5cm，
∴BP＝AB﹣AP＝（5﹣t）cm，
∵∠CAB＝∠DBA，
∴①当AC＝BP＝3cm，AP＝BQ＝t cm时，△ACP与△BPQ全等，
∴5﹣t＝3，
∴t＝2，
∴AP＝BQ＝2cm，
∴点Q的运动速度＝＝1（cm/s）；
②当AC＝BQ＝3cm，AP＝BP时，△ACP与△BPQ全等，
∴t＝5﹣t，
∴t＝2.5，
∴点Q的运动速度＝＝（cm/s）；
综上所述：当点Q的运动速度为1或cm/s时，△ACP与△BPQ有可能全等，
故答案为：1或．
【点评】本题考查了全等三角形的判定，分两种情况讨论是解题的关键．
三、解答题
17．（6分）已知一个多边形的内角和与外角和的和为1080°，且这个多边形的各个内角都相等．求这个多边形的每个外角度数．
【分析】设这个多边形是n边形，它的内角和可以表示成（n﹣2）•180°，就得到关于n的方程，求出边数n．然后根据多边形的外角和是360°，多边形的每个内角都相等即每个外角也相等，这样就能求出多边形的一个外角．
【解答】解：设这个多边形是n边形，
根据题意得：（n﹣2）•180°+360°＝1080°，
解得n＝6；
那么这个多边形的一个外角是360°÷6＝60°，
即这个多边形的每个外角的度数是60°．
【点评】考查了多边形内角与外角，根据多边形的内角和定理，求边数的问题就可以转化为解方程的问题来解决．同时考查了多边形内角与外角的关系．
18．（6分）已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，
且∠1＝∠A．若∠BFE＝110°，∠1＝60°，求∠B的度数．
【分析】由三角形的外角公式可求出∠D，AB∥DC可推得∠D＝∠B．
【解答】解：∵∠BFE＝∠1+∠D，
∴∠D＝∠BFE﹣∠1＝110°﹣60°＝50°，
∵AB∥DC
∴∠B＝∠D，
∴∠B＝50°．
【点评】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键．
19．（7分）如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC．求证：△ABC≌△ADE．
【分析】根据题意，得到∠BAC＝∠EAD，在△ABC和△ADE中，利用SAS得到△ABC≌△ADE，由此得到证明．
【解答】证明：∵∠BAD＝∠CAE＝90°，
∴∠BAC+∠CAD＝∠EAD+∠CAD，
∴∠BAC＝∠EAD，
在△ABC和△ADE中，
，
∴△ABC≌△ADE（SAS）．
【点评】本题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解答本题的关键．
20．（7分)在直角三角形ABC中，∠ACB＝90°，CD是AB边上的高，AB＝10cm，BC＝8cm，AC＝6cm
（1）求△ABC的面积；
（2）求CD的长；
（3）若△ABC的边AC上的中线是BE，求出△ABE的面积．
【分析】（1）先画图，根据直角三角形面积的求法，即可得出△ABC的面积；
（2）根据三角形的面积公式即可求得CD的长；
（3）根据中线的性质可得出△ABE和△BCE的面积相等，从而得出答案．
【解答】解：（1）∵∠ACB＝90°，BC＝8cm，AC＝6cm，
∴S△ABC＝AC•BC＝×6×8＝24；
（2）∵S△ABC＝×AB×CD＝24，
∴CD＝4.8cm；
（3）∵AE＝CE，
∴S△ABE＝S△BCE＝S△ABC＝12，
∴△ABE的面积为12cm2．
【点评】本题考查了勾股定理的逆定理和三角形面积的计算，是基础知识要熟练掌握．
21．(8分）已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD．
（1）求证：∠E＝∠F；
（2）若∠A＝40°，∠D＝80°，求∠E的度数．
【分析】（1）首先利用平行线的性质得出，∠A＝∠FBD，根据AB＝CD即可得出AC＝BD，进而得出△EAC≌△FBD解答即可；
（2）根据全等三角形的性质和三角形内角和解答即可．
【解答】证明：（1）∵EA∥FB，
∴∠A＝∠FBD，
∵AB＝CD，
∴AB+BC＝CD+BC，
即AC＝BD，
在△EAC与△FBD中，
，
∴△EAC≌△FBD（SAS），
∴∠E＝∠F；
（2）∵△EAC≌△FBD，
∴∠ECA＝∠D＝80°，
∵∠A＝40°，
∴∠E＝180°﹣40°﹣80°＝60°，
答：∠E的度数为60°．
【点评】此题主要考查了全等三角形的判定与性质等知识，解题时注意：两边及其夹角分别对应相等的两个三角形全等．根据已知得出△EAC≌△FBD是解题关键．
22．（8分）如图，在四边形ABCD中，点E为对角线BD上一点，∠A＝∠BEC，AD∥BC，且AD＝BE．
（1）证明：△ABD≌△ECB；
（2）若BC＝15，AD＝6，请求出DE的长度．
【分析】（1）由AD∥BC，得∠ADB＝∠EBC，即可根据全等三角形的判定定理“ASA”证明△ABD≌△ECB；
（2）由△ABD≌△ECB，得DB＝BC＝15，AD＝EB＝6，即可由DE＝DB﹣EB求得DE的长度为9．
【解答】（1）证明：∵AD∥BC，
∴∠ADB＝∠EBC，
在△ABD和△ECB中，
，
∴△ABD≌△ECB（ASA）．
（2）解：△ABD≌△ECB，
∴DB＝BC＝15，AD＝EB＝6，
∴DE＝DB﹣EB＝15﹣6＝9，
∴DE的长度是9．
【点评】此题重点考查平行线的性质、全等三角形的判定与性质等知识，正确地找到全等三角形的对应边和对应角并且证明∠ADB＝∠EBC是解题的关键．
23．（10分）如图①，在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥MN于点M，BN⊥MN于点N．
（1）求证：MN＝AM+BN；
（2）如图②，若过点C作直线MN与线段AB相交，AM⊥MN于点M，BN⊥MN于点N（AM＞BN），（1）中的结论是否仍然成立？若不成立，请写出正确的结论，并说明理由．
【分析】（1）先根据垂直的定义得到∠AMC＝∠CNB＝90°，则∠MAC+∠ACM＝90°，又∠ACB＝90°，则∠ACM+∠NCB＝90°，于是根据等量代换得到∠MAC＝∠NCB，根据“AAS”可证明△ACM≌△CBN，根据全等的性质得AM＝CN，CM＝BN，则MN＝MC+CN＝AM+BN；
（2）与（1）证明方法一样可得到△ACM≌△CBN，根据全等的性质得AM＝CN，CM＝BN，而MN＝CN﹣CM＝AM﹣BN．
【解答】证明：（1）∵AM⊥MN于M，过B作BN⊥MN于N，
∴∠AMC＝∠CNB＝90°，
∴∠MAC+∠ACM＝90°，
∵∠ACB＝90°，
∴∠ACM+∠NCB＝90°，
∴∠MAC＝∠NCB，
∵在△ACM和△CBN中，
，
∴△ACM≌△CBN（AAS），
∴AM＝CN，CM＝BN，
∴MN＝MC+CN＝AM+BN；
（2）（1）中的结论不成立，MN与AM、BN之间的数量关系为MN＝AM﹣BN．理由如下：
∵AM⊥MN于M，过B作BN⊥MN于N，
∴∠AMC＝∠CNB＝90°，
∴∠MAC+∠ACM＝90°，
∵∠ACB＝90°，
∴∠ACM+∠NCB＝90°，
∴∠MAC＝∠NCB，
在△ACM和△CBN中，
，
∴△ACM≌△CBN（AAS），
∴AM＝CN，CM＝BN，
∴MN＝CN﹣CM＝AM﹣BN．
【点评】本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．