北京市人大附中朝阳分校2024年数学九年级第一学期开学调研模拟试题【含答案】

这是一份北京市人大附中朝阳分校2024年数学九年级第一学期开学调研模拟试题【含答案】，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知平面上四点，，，，一次函数的图象将四边形ABCD分成面积相等的两部分，则
A．2B．C．5D．6
2、（4分）小红把一枚硬币抛掷10次，结果有4次正面朝上，那么（ ）
A．正面朝上的频数是0.4
B．反面朝上的频数是6
C．正面朝上的频率是4
D．反面朝上的频率是6
3、（4分）下列多边形中，不能够单独铺满地面的是（ ）
A．正三角形B．正方形C．正五边形D．正六边形
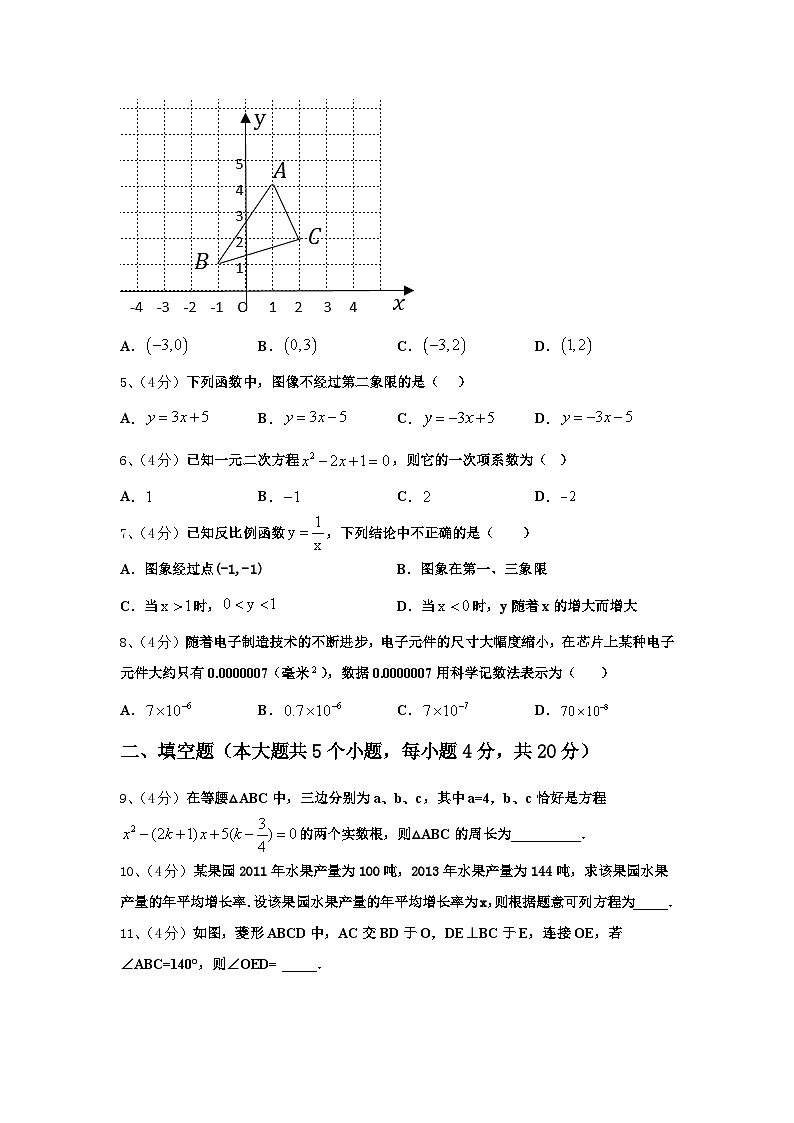
4、（4分）如图，的顶点坐标分别为，，，如果将先向左平移个单位，再向上平移个单位得到，那么点的对应点的坐标是（ ）
A．B．C．D．
5、（4分）下列函数中，图像不经过第二象限的是（ ）
A．B．C．D．
6、（4分）已知一元二次方程，则它的一次项系数为（ ）
A．B．C．D．
7、（4分）已知反比例函数，下列结论中不正确的是（ ）
A．图象经过点(-1,-1)B．图象在第一、三象限
C．当时，D．当时，y随着x的增大而增大
8、（4分）随着电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只有0.0000007（毫米），数据0.0000007用科学记数法表示为（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）在等腰△ABC中，三边分别为a、b、c，其中a=4，b、c恰好是方程的两个实数根，则△ABC的周长为__________．
10、（4分）某果园2011年水果产量为100吨，2013年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x，则根据题意可列方程为_____．
11、（4分）如图，菱形ABCD中，AC交BD于O，DE⊥BC于E，连接OE，若∠ABC=140°，则∠OED= _____．
12、（4分）若代数式有意义，则x的取值范围是__________．
13、（4分）已知一次函数的图象过点（3，5）与点（-4，-9），则这个一次函数的解析式为____________.
三、解答题（本大题共5个小题，共48分）
14、（12分）甲、乙两人加工一种零件，甲比乙每小时多加工10个零件，甲加工150个零件所用的时间与乙加工120个零件所用的时间相等．
（1）求甲每小时加工多少个零件？
（2）由于厂家在12小时内急需一批这种零件不少于1000件，决定由甲、乙两人共同完成．乙临时有事耽搁了一段时间，先让甲单独完成一部分零件后两人合作完成剩下的零件．求乙最多可以耽搁多长时间？
15、（8分）如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
16、（8分）如图，在平面直角坐标系中，一次函数的图象与正比例函数的图象都经过点．
（1）求一次函数和正比例函数的解析式；
（2）若点是线段上一点，且在第一象限内，连接，设的面积为，求面积关于的函数解析式．
17、（10分）问题发现：
（1）如图①，正方形ABCD的边长为4，对角线AC、BD相交于点O，E是AB上点（点E不与A、B重合），将射线OE绕点O逆时针旋转90°，所得射线与BC交于点F，则四边形OEBF的面积为 ．
问题探究：
（2）如图②，线段BQ＝10，C为BQ上点，在BQ上方作四边形ABCD，使∠ABC＝∠ADC＝90°，且AD＝CD，连接DQ，求DQ的最小值；
问题解决：
（3）“绿水青山就是金山银山”，某市在生态治理活动中新建了一处南山植物园，图③为南山植物园花卉展示区的部分平面示意图，在四边形ABCD中，∠ABC＝∠ADC＝90°，AD＝CD，AC＝600米．其中AB、BD、BC为观赏小路，设计人员考虑到为分散人流和便观赏，提出三条小路的长度和要取得最大，试求AB+BD+BC的最大值．
18、（10分）如图，在12×12的正方形网格中，△TAB 的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）．
（1）以点T（1，1）为位似中心，按比例尺（TA′∶TA）3∶1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′．画出△TA′B′，并写出点A′、B′的坐标；
（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）在平行四边形ABCD中，若∠A+∠C=140°，则∠B= ．
20、（4分）如图，在平面直角坐标系中有两点A（6，0），B（0，3），如果点C在x轴上（C与A不重合），当点C的坐标为 时，△BOC与△AOB相似．
21、（4分）如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为40，则OH的长等于_____．
22、（4分）已知平行四边形ABCD中，∠B＋∠D＝270°，则∠C＝________.
23、（4分）如图，△ABC中，已知AB=8，∠C=90°，∠A=30°，DE是中位线，则DE的长为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）在菱形ABCD中，∠ABC=60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化.
(1)探索发现
如图1，当点E在菱形ABCD内部时，连接CE，BP与CE的数量关系是_______，CE与AD的位置关系是_______.
(2)归纳证明
证明2，当点E在菱形ABCD外部时，(1)中的结论是否还成立?若成立，请予以证明；若不成立，请说明理由.
(3)拓展应用
如图3，当点P在线段BD的延长线上时，连接BE，若AB=5，BE=13，请直接写出线段DP的长.
25、（10分）实践与探究
宽与长的比是（约0.618）的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。
下面我们通过折纸得到黄金矩形。
第一步，在一张矩形纸片的一端，利用图1的方法折出一个正方形，然后把纸片展平。
第二步，如图2，把这个正方形折成两个相等的矩形，再把纸片展平，折痕是。
第三步，折出内侧矩形的对角线，并把折到图3中所示的处，折痕为。
第四步，展平纸片，按照所得的点折出，使；过点折出折痕，使。
（1）上述第三步将折到处后，得到一个四边形，请判断四边形的形状，并说明理由。
（2）上述第四步折出折痕后得到一个四边形，这个四边形是黄金矩形，请你说明理由。（提示：设的长度为2）
（3）在图4中，再找出一个黄金矩形_______________________________（黄金矩形除外，直接写出答案，不需证明，可能参考数值：）
（4）请你举一个采用了黄金矩形设计的世界名建筑_________________________.
26、（12分）在进行二次根式化简时，我们有时会碰上如，，一样的式子，其实我们还可以将其进一步化简：，，；以上这种化简的步骤叫做分母有理化.还可以用以下方法化简：
（1）请用不同的方法化简；（2）化简：.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
根据题意四边形ABCD是矩形，直线只要经过矩形对角线的交点，即可得到k的值．
【详解】
，，，，
，，
四边形ABCD是平行四边形，，
四边形ABCD是矩形，
对角线AC、BD的交点坐标为，
直线经过点时，直线将四边形ABCD的面积分成相等的两部分，
，
．
故选：B．
本题考查矩形的判定和性质、一次函数图象上点的坐标特征等知识，掌握中心对称图形的性质是解决问题的关键．
2、B
【解析】
小红做抛硬币的实验，共抛了10次，4次正面朝上，6次反面朝上，则正面朝上的频数是4，反面朝上的频数是6.
故选B.
3、C
【解析】
由镶嵌的条件知，在一个顶点处各个内角和为360°．
【详解】
∵正三角形的内角=180°÷3=60°，360°÷60°=6，即6个正三角形可以铺满地面一个点，∴正三角形可以铺满地面；
∵正方形的内角=360°÷4=90°，360°÷90°=4，即4个正方形可以铺满地面一个点，∴正方形可以铺满地面；
∵正五边形的内角=180°－360°÷5=108°，360°÷108°≈3.3，∴正五边形不能铺满地面；
∵正六边形的内角=180°－360°÷6=120°，360°÷120°=3，即3个正六边形可以铺满地面一个点，∴正六边形可以铺满地面．
故选C．
几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．
4、C
【解析】
把B点的横坐标减2，纵坐标加1即为点B´的坐标．
【详解】
解：由题中平移规律可知：点B´的横坐标为-1−2=−3；纵坐标为1+1=2，
∴点B´的坐标是(−3,2)．
故选：C．
本题考查了坐标与图形变化−平移，平移变换是中考的常考点，平移中点的变化规律是：左右移动改变点的横坐标，左减右加；上下移动改变点的纵坐标，下减上加．
5、B
【解析】
根据一次函数的性质，逐个进行判断，即可得出结论．
【详解】
各选项分析得：
A. k=3>0，b=5>0，图象经过第一、二、三象限；
B. k=3>0，b=−5<0，图象经过第一、三、四象限；
C. k=−3<0，b=5>0，图象经过第一、二、四象限；
D. k=−3<0，b=−5<0，图象经过第二、三、四象限.
故选B.
此题考查一次函数的性质，解题关键在于掌握一次函数的性质.
6、D
【解析】
根据一般地，任何一个关于x的一元二次方程经过整理，都能化成如下形式ax2+bx+c=0（a≠0）．这种形式叫一元二次方程的一般形式．其中ax2叫做二次项，a叫做二次项系数；bx叫做一次项；c叫做常数项可得答案．
【详解】
解：一元二次方程，则它的一次项系数为-2，
故选：D．
此题主要考查了一元二次方程的一般形式，关键是掌握一元二次方程的一般形式为ax2+bx+c=0（a≠0）．
7、D
【解析】
根据反比例函数的性质，利用排除法求解．
【详解】
解：A、x=-1，y==-1，∴图象经过点（-1，-1），正确；
B、∵k=1＞0，∴图象在第一、三象限，正确；
C、∵k=1＞0，∴图象在第一象限内y随x的增大而减小，∴当x＞1时，0＜y＜1，正确；
D、应为当x＜0时，y随着x的增大而减小，错误．
故选：D．
本题考查了反比例函数的性质，当k＞0时，函数图象在第一、三象限，在每个象限内，y的值随x的值的增大而减小．
8、C
【解析】
科学记数法就是将一个数字表示成（a×10的n次幂的形式），其中1≤|a|＜10，n表示整数．即从左边第一位开始，在首位非零的后面加上小数点，再乘以10的n次幂．本题0.000 000 1＜1时，n为负数．
【详解】
0.000 000 1=1×10-1．
故选C．
此题考查的是电子原件的面积，可以用科学记数法表示，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、9或10.1
【解析】
根据等腰△ABC中，当a为底，b，c为腰时，b=c，得出△=[-（2k+1）]2-4×1（k-）=4k2+4k+1-20k+11=4k2-16k+16=0，解方程求出k=2，则b+c=2k+1=1；当a为腰时，则b=4或c=4，然后把b或c的值代入计算求出k的值，再解方程进而求解即可．
【详解】
等腰△ABC中，当a为底，b，c为腰时，b=c，若b和c是关于x的方程x2-（2k+1）x+1（k-）=0的两个实数根，
则△=[-（2k+1）]2-4×1（k-）=4k2+4k+1-20k+11=4k2-16k+16=0，
解得：k=2，
则b+c=2k+1=1，
△ABC的周长为4+1=9；
当a为腰时，则b=4或c=4，
若b或c是关于x的方程x2-（2k+1）x+1（k-）=0的根，
则42-4（2k+1）+1（k-）=0，
解得：k=，
解方程x2-x+10=0，
解得x=2.1或x=4，
则△ABC的周长为：4+4+2.1=10.1．
10、100（1+x）2=1
【解析】分析：2013年的产量=2011年的产量×（1+年平均增长率）2，把相关数值代入即可．
详解：设该果园水果产量的年平均增长率为x，根据题意，得：
100（1+x）2=1，
故答案为：100（1+x）2=1．
点睛：本题考查了由实际问题抽象出一元二次方程；得到2013年产量的等量关系是解决本题的关键．
11、20°
【解析】
解：∵四边形ABCD是菱形，∴DO=OB，∵DE⊥BC于E，∴OE为直角三角形BED斜边上的中线，∴OE=BD，∴OB=OE，∴∠OBE=∠OEB，∵∠ABC=140°，∴∠OBE=70°，∴∠OED=90°﹣70°=20°，故答案为20°．
点睛：本题考查了菱形的性质、直角三角形斜边上中线的性质，得到OE为直角三角形BED斜边上的中线是解题的关键．
12、且
【解析】
结合二次根式和分式有意义的条件，列式求解即可得到答案；
【详解】
解：∵代数式有意义，
∴，
解得：且，
故答案为：且．
本题主要考查了二次根式和分式有意义的条件；对于二次根式，被开方数不能为负；对于分式，分母不能为0；掌握这两个知识点是解题的关键．
13、
【解析】
设一次函数的解析式为：，利用待定系数法把已知点的坐标代入解析式，解方程组即可得答案．
【详解】
解：设一次函数的解析式为：，

解得：
所以这个一次函数的解析式为：
故答案为：
本题考查的是利用待定系数法求解一次函数的解析式，掌握待定系数法是解题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）甲每小时加工50个零件，则乙每小时加工40个零件；（2）2小时．
【解析】
(1)主要利用甲加工150个零件所用的时间与乙加工120个零件所用的时间相等，建立等式关系，即可求解，
(2)乙最多可以耽搁多长时间，这是一个不等式，把乙的完成的工作量+甲完成的工作量≥1000，
【详解】
解：（1）设甲每小时加工x个零件，则乙每小时加工（x﹣10）个零件，
根据题意，得：＝，
解得：x＝50，
经检验x＝50是分式方程的解，
答：甲每小时加工50个零件，则乙每小时加工40个零件；
（2）设乙耽搁的时间为x小时，
根据题意，得：50x+（50+40）（12﹣x）≥1000，
解得：x≤2，
答：乙最多可以耽搁2小时．
本题主要考查分式方程和一元一次不等式的实际应用
15、（1）证明见解析；（2）1．
【解析】
（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
【详解】
证明：（1）∵D、G分别是AB、AC的中点，∴DG∥BC，DG=BC，
∵E、F分别是OB、OC的中点，
∴EF∥BC，EF=BC，
∴DE=EF，DG∥EF，
∴四边形DEFG是平行四边形；
（2）∵∠OBC和∠OCB互余，
∴∠OBC+∠OCB=90°，
∴∠BOC=90°，
∵M为EF的中点，OM=3，
∴EF=2OM=1．
由（1）有四边形DEFG是平行四边形，∴DG=EF=1．
16、（1）y=﹣x+4，；（2）S=2x（0＜x≤3）．
【解析】
（1）把B（3，1）分别代入y=﹣x+b和y=kx即可得到结论；
（2）根据三角形的面积公式即可得到结论．
【详解】
（1）把B（3，1）分别代入y=﹣x+b和y=kx得1=﹣3+b，1=3k，解得：b=4，k，∴y=﹣x+4，yx；
（2）∵点P（x，y）是线段AB上一点，∴S•xP2x（0＜x≤3）．
本题考查了两直线相交或平行，三角形面积的求法，待定系数法确定函数关系式，正确的理解题意是解题的关键．
17、（1）4；（2）5；（3）600（+1）．
【解析】
（1）如图①中，证明△EOB≌△FOC即可解决问题；
（2）如图②中，连接BD，取AC的中点O，连接OB，OD．利用四点共圆，证明∠DBQ＝∠DAC＝45°，再根据垂线段最短即可解决问题．
（3）如图③中，将△BDC绕点D顺时针旋转90°得到△EDA，首先证明AB+BC+BD＝（+1）BD，当BD最大时，AB+BC+BD的值最大．
【详解】
解：（1）如图①中，
∵四边形ABCD是正方形，
∴OB＝OC，∠OBE＝∠OCF＝45°，∠BOC＝90°，
∵∠EOF＝90°，
∴∠EOF＝∠BOC，
∴∠EOB＝∠FOC，
∴△EOB≌△FOC（SAS），
∴S△EOB＝S△OFC，
∴S四边形OEBF＝S△OBC＝•S正方形ABCD＝4，
故答案为：4；
（2）如图②中，连接BD，取AC的中点O，连接OB，OD．
∵∠ABD＝∠ADC＝90°，AO＝OC，
∴OA＝OC＝OB＝OD，
∴A，B，C，D四点共圆，
∴∠DBC＝∠DAC，
∵DA＝DC，∠ADC＝90°，
∴∠DAC＝∠DCA＝45°，
∴∠DBQ＝45°，
根据垂线段最短可知，当QD⊥BD时，QD的值最短，DQ的最小值＝BQ＝5．
（3）如图③中，将△BDC绕点D顺时针旋转90°得到△EDA，
∵∠ABC+∠ADC＝180°，
∴∠BCD+∠BAD＝∠EAD+BAD＝180°，
∴B，A，E三点共线，
∵DE＝DB，∠EDB＝90°，
∴BE＝BD，
∴AB+BC＝AB+AE＝BE＝BD，
∴BC+BC+BD＝（+1）BD，
∴当BD最大时，AB+BC+BD的值最大，
∵A，B，C，D四点共圆，
∴当BD为直径时，BD的值最大，
∵∠ADC＝90°，
∴AC是直径，
∴BD＝AC时，AB+BC+BD的值最大，最大值＝600（+1）．
本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，四点共圆，圆周角定理，垂线段最短等知识，解题的关键是学会添加常用辅助线面构造全等三角形解决问题，学会用转化的思想思考问题，属于中考常考题型．
18、（1）A′坐标为（4，7），B′坐标为（10，4）；（2）点C′的坐标为(3a－2，3b－2 ) ．
【解析】
（1）根据题目的叙述，正确地作出图形，然后确定各点的坐标即可；（2）由（1）中坐标分析出x值变化=3x-2，y值变化=3y-2，从而使问题得解．
【详解】
解：（1）依题意知，以点T（1,1）为位似中心，按比例尺（TA′：TA）3:1的位似中心的同侧将TAB放大为△TA′B′，故TA′=3TA， B′T=3BT．则延长如图，连结A’B’得△TA′B′．
由图可得A′坐标为（4,7），B′坐标为（10，4）；
（2） 易知A、B坐标由A（2,3），B（4,2）变化为A′（4,7），B′（10，4）；
则x值变化=3x-2，y值变化=3y-2；
若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标，则变化后点C的对应点C′的坐标为：C′（3a-2，3b-2）
本题难度中等，主要考查了作图-位似变换，正确理解位似变换的定义，会进行位似变换的作图是解题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、110°
【解析】
试题解析：∵平行四边形ABCD，
∴∠A+∠B=180°，∠A=∠C，
∵∠A+∠C=140°，
∴∠A=∠C=70°，
∴∠B=110°．
考点：平行四边形的性质．
20、（﹣1.5，0），（1.5，0），（﹣6，0）
【解析】
本题可从两个三角形相似入手，根据C点在x轴上得知C点纵坐标为0，讨论OC与OA对应以及OC与OB对应的情况，分别讨论即可．
【详解】
解：∵点C在x轴上，
∴∠BOC=90°，两个三角形相似时，应该与∠BOA=90°对应，
若OC与OA对应，则OC=OA=6，C（﹣6，0）；
若OC与OB对应，则OC=1.5，C（﹣1.5，0）或者（1.5，0）．
∴C点坐标为：（﹣1.5，0），（1.5，0），（﹣6，0）．
故答案为（﹣1.5，0），（1.5，0），（﹣6，0）．
考点：相似三角形的判定；坐标与图形性质．
21、2
【解析】
首先求得菱形的边长，则OH是直角△AOD斜边上的中线，依据直角三角形的性质即可求解．
【详解】
AD＝×40＝1．
∵菱形ANCD中，AC⊥BD．
∴△AOD是直角三角形，
又∵H是AD的中点，
∴OH＝AD＝×1＝2．
故答案是：2．
本题考查了菱形的性质和直角三角形的性质，直角三角形斜边上的中线等于斜边的一半．
22、45°
【解析】
试题解析：∵四边形ABCD为平行四边形，
∴AD∥BC，∠B=∠D，
且


故答案为
点睛：平行四边形的对角相等，邻角互补.
23、2
【解析】
先由含30°角的直角三角形的性质,得出BC,再由三角形的中位线定理得出DE即可.
【详解】
因为，△ABC中，∠C=90°，∠A=30°，
所以， ,
因为，DE是中位线，
所以，.
故答案为2
本题考核知识点：直角三角形，三角形中位线. 解题关键点：熟记直角三角形性质，三角形中位线性质.
二、解答题（本大题共3个小题，共30分）
24、 (1)BP=CE，CE⊥AD；(2)(1)中的结论仍成立.理由见解析； (3)PD= ．
【解析】
（1）由菱形ABCD和∠ABC=60°可证△ABC与△ACD是等边三角形，由等边△APE可得AP=AE，∠PAE=∠BAC=60°，减去公共角∠PAC得∠BAP=∠CAE，根据SAS可证得△BAP≌△CAE，故有BP=CE，∠ABP=∠ACE．由菱形对角线平分一组对角可证∠ABP=30°，故∠ACE=30°即CE平分∠ACD，由AC=CD等腰三角形三线合一可得CE⊥AD．
（2）证明过程同（1）．
（3）由AB=5即△ABC为等边三角形可求得BD的长．连接CE，由（2）可求∠BCE=90°，故在Rt△BCE中，由勾股定理可求CE的长．又由（2）可得BP=CE，由DP=BP-BD即求得DP的长．
【详解】
解：(1) ∵菱形ABCD中，∠ABC=60°
∴AB=BC=CD=AD，∠ADC=∠ABC=60°
∴△ABC、△ACD是等边三角形
∴AB=AC，AC=CD，∠BAC=∠ACD=60°
∵△APE是等边三角形
∴AP=AE，∠PAE=60°
∴∠BAC-∠PAC=∠PAE-∠PAC
即∠BAP=∠CAE
在△BAP与△CAE中

∴△BAP≌△CAE（SAS）
∴BP=CE，∠ABP=∠ACE
∵BD平分∠ABC
∴∠ACE=∠ABP=∠ABC=30°
∴CE平分∠ACD
∴CE⊥AD
故答案为：BP=CE，CE⊥AD；
(2)(1)中的结论仍成立，证明如下：
设AD与CE交于点O
∵四边形ABCD为菱形，且∠ABC=60°
∴△ABC为等边三角形.
∴AB=AC，∠BAC=60°
∴∠BAP=∠CAE
又∵ΔAPE为等边三角形
∴AP=AE
在△BAP与△CAE中
∴△BAP≌ΔCAE(SAS)
∴BP=CE
∴∠ACE=∠ABP=30°
又∵∠CAD=60°
∠A0C=90°
∴AD⊥CE；
(3) 连接CE，设AC与BD相交于点O
∵AB=5
∴BC=AC=AB=5
∴AO=AC=
∴BO= ＝＝
∴BD=2BO=5
∵∠BCE=∠BCA+∠ACE=90°，BE=13
∴CE= ＝=12
由（2）可知，BP=CE=12
∴DP=BP-BD=12-5
故答案为：(1)BP=CE，CE⊥AD；(2)(1)中的结论仍成立.理由见解析； (3)PD= ．
本题考查菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理．第（2）题的证明过程可由（1）适当转化而得，第（3）题则可直接运用（2）的结论解决问题．
25、（1）四边形是菱形，见解析；（2）见解析；（3）黄金矩形（或黄金矩形）；（4）希腊的巴特农神庙（或巴黎圣母院）.
【解析】
（1）根据菱形的判定即可求解；
（2）根据菱形的性质及折叠得到，即可证明；
（3）
【详解】
（1）解：
四边形是菱形，
理由如下：
由矩形纸片可得，
∴，
由折叠可得，
∴，
∴，
又由折叠可得，
∴，
∴四边形是菱形；
（2）证明：设的长度为2，
由正方形可得，，
∴，
∵，
∴，
∴，
∴四边形是矩形，
∵，由折叠可得，，
在中，根据勾股定理，，
由折叠可得，
∴，
∴，
∴矩形是黄金矩形；
（3）黄金矩形
理由：AG=AD+DG=AB+DG=
AH=2，
∴
∴四边形AGEH为黄金矩形
（4）希腊的巴特农神庙（或巴黎圣母院）
此题主要考查矩形的性质与判定，解题的关键是熟知特殊平行四边形的判定与性质.
26、（1）；（2）.
【解析】
试题分析：（1）分式的分子和分母都乘以，即可求出答案；把2看出5-3，根据平方差公式分解因式，最后进进约分即可．
（2）先每一个二次根式分母有理化，再分母不变，分子相加，最后合并即可．
试题解析：（1）①
②；
（2）原式=
=.
考点：分母有理化．
题号
一
二
三
四
五
总分
得分
批阅人