上海市华东师范大学松江实验高级中学2024-2025学年高三上学期10月检测数学试题(无答案)

这是一份上海市华东师范大学松江实验高级中学2024-2025学年高三上学期10月检测数学试题(无答案)，共4页。试卷主要包含了10）等内容，欢迎下载使用。

（2024.10）
（完卷时间120分钟，试卷分值：150分，命题：徐素琳 杜佳伟）
一､填空题（本大题满分54分）本大题共有12题，第1~6题每题4分，第7~12题每题5分.
1.已知全集，则__________.
2.函数的定义域是__________.
3.已知角的顶点在坐标原点，始边在轴的正半轴上，终边上一点，则__________.
4.函数是幂函数，且上为减函数，则实数的值是__________.
5.不等式恒成立，则的取值范围是__________.
5.已知函数，则__________.
6.已知，则的最小值为__________.
7.已知是方程的两个实数根，则__________.
8.在中，若，则这个三角形是__________三角形.
9.已知函数，对任意，都有（为常数），且当时，，则__________.
10.函数在区间上是单调函数，则实数的取值范围是__________.
11.如果函数在区间上是增函数，且函数在区间上是减函数，那么称函数是区间上的“缓增函数”，区间叫做“缓增区间”.若函数是区间上的“缓增函数”，则“缓增区间”为__________.
二､选择题（本大题满分18分）本大题共有4题，每题有且只有一个正确答案，第13､14题选对得4分，第15､16题选对得5分，否则一律得零分.
13.已知，使成立的一个充分不必要条件是（ ）
A. B.
C. D.
14.已知是三角形的内角，若，则的值等于（ ）
A. B. C. D.
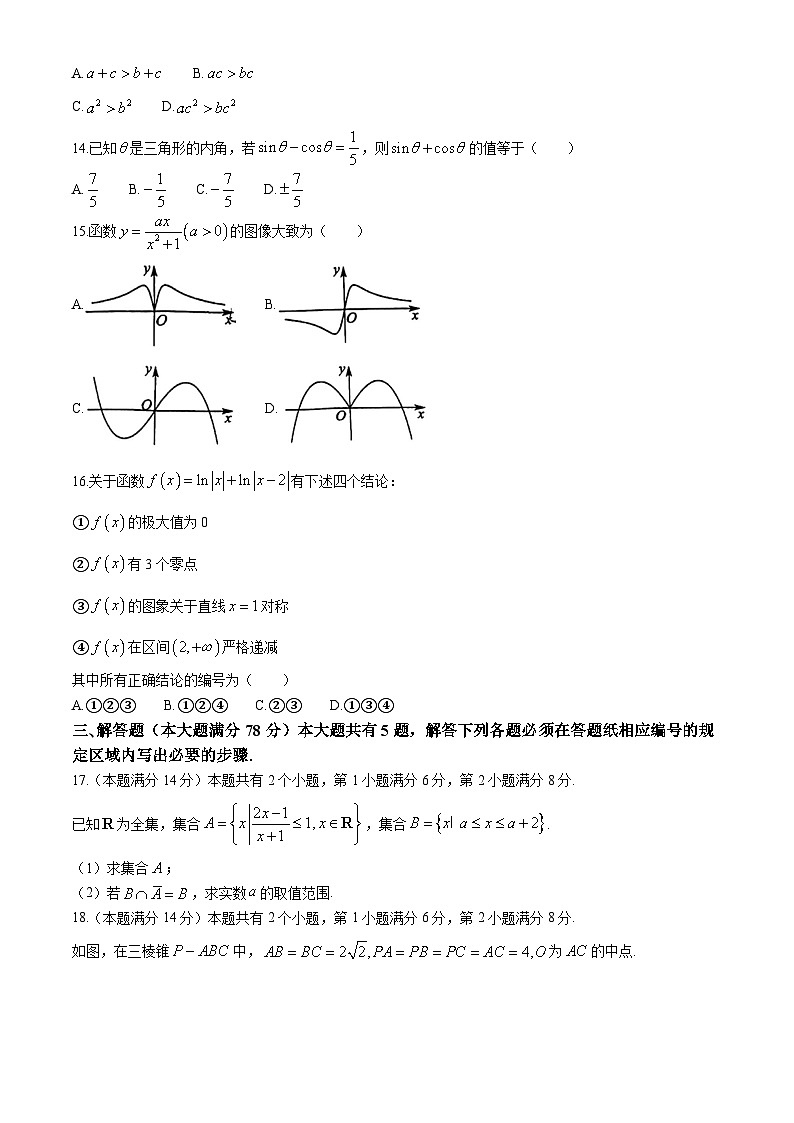
15.函数的图像大致为（ ）
A. B.
C. D.
16.关于函数有下述四个结论：
①的极大值为0
②有3个零点
③的图象关于直线对称
④在区间严格递减
其中所有正确结论的编号为（ ）
A.①②③ B.①②④ C.②③ D.①③④
三､解答题（本大题满分78分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
17.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
已知为全集，集合，集合.
（1）求集合；
（2）若，求实数的取值范围.
18.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
如图，在三棱锥中，为的中点.
（1）证明：平面；
（2）若点在棱上，且，求点到平面的距离.
19.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
为了在夏季降温和冬季供暖时减少能源耗损，建筑物的外墙需要建造隔热层，现某建筑物要建造可使用20年的隔热层，已知每厘米厚的隔热层建造成本为5万元，该建筑物每年的能源消耗费用（单位：万元）与隔热层厚度（单位：cm）满足关系，若不建隔热层，则该建筑物每年的能源消费费用为6万元，设为隔热层建造费用与20年的能源消耗费用之和.
（1）请写出函数的表达式；
（2）当隔热层多厚时，达到最小，并求出其最小值.
20.（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.
已知函数.
（1）若曲线在点处的切线为轴，求的值；
（2）讨论在区间内的极值点个数：
（3）若，求证：存在两个零点，且满足.
21.（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.
设函数的定义域为，对于区间，当且仅当函数满足以下①②两个性质中的任意一个时，则称区间是的一个“美好区间”.
性质①：对于任意，都有；性质②：对于任意，都有.
（1）已知.分别判断区间和区间是否为函数的“美好区间”，并说明理由；
（2）已知且，若区间是函数的一个“美好区间”，求实数的取值范围；
（3）已知函数的定义域为，其图像是一条连续不断的曲线，且对于任意，都有.求证：函数存在“美好区间”，且存在，使得不属于函数的任意一个“美好区间”.