初中数学浙教版（2024）七年级上册（2024）2.3 有理数的乘法精品ppt课件

这是一份初中数学浙教版（2024）七年级上册（2024）2.3 有理数的乘法精品ppt课件，文件包含231有理数的乘法pptx、核心素养教学设计docx、核心素养导学案docx等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

1.贴近生活实例感受有理数的乘法，理解有理数乘法法则2.能判断多个有理数相乘时积的符号3.理解倒数的概念
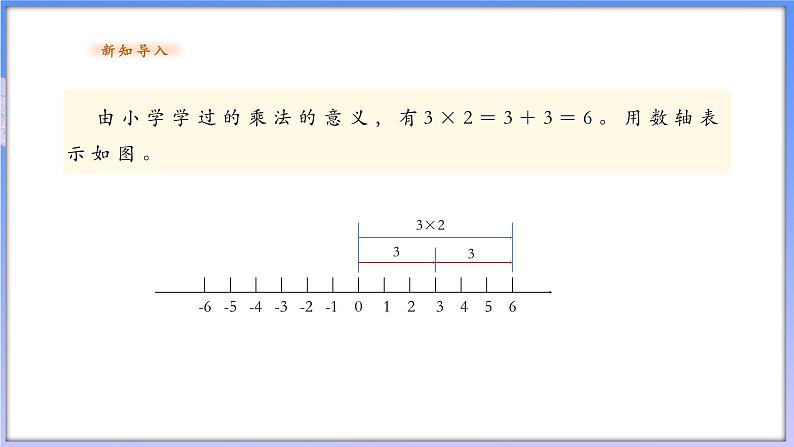
由小学学过的乘法的意义，有3×2＝3＋3＝6。用数轴表示如图。
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
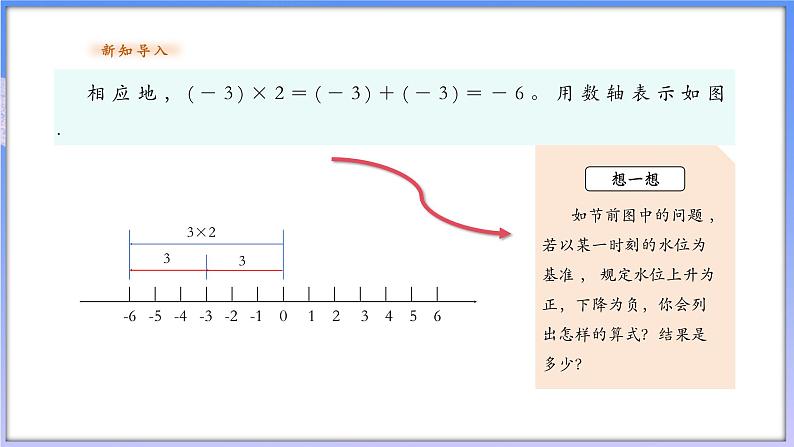
相应地，(－3)×2＝(－3)＋(－3)＝－6。用数轴表示如图.
如节前图中的问题 ，若以某一时刻的水位为基准 ， 规定水位上升为正，下降为负，你会列出怎样的算式？结果是多少？
做一做(1)完成下列填空：4×2＝_______； (－4)×2＝_______＋_______＝_______ (用数轴表示)；5×2＝_______； (－5)×2＝_______＋_______＝_______；6×2＝_______； (－6)×2＝_______＋_______=_______ 。
8 -4 -4 -810 -5 -5 -1012 -6 -6 -12
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
做一做(2)观察上面左右两列算式中相乘两数及计算结果的符号，你有什么发现?
我们发现，当我们改变相乘两数中一个数的符号时，其积就变为原来积 的相反数例如,(－3)×2＝－(3×2)。 同样，3×(－2)的积也应是3×2的积的相反数，即3×(－2)＝－(3×2)＝－6,用数轴表示如图.
同样，(－3)×(－2)的积是3×(－2)的积的相反数，即(－3)×(－2)＝ 3×2＝6，用数轴表示如图.
根据生活经验，我们也可以获得相同的结论，比如水库的水位每天下降 3厘米，那么2天前的水位比现在的水位高6厘米。如果把水位下降3厘米记为(－3)厘米，2天前记为(－2)天，那么根据实际意义，可知(－3)×(－2)＝＋6。
做一做写出下列各算式的结果：3×7＝_______ ；(－3)×7＝ _______ ；3×(－7)＝ _______ ；(－3)×(－7)＝ _______ ；0×7＝ _______ ；0×(－7)＝ _______ 。由此你认为两个数相乘，积的符号与这两个数的符号有什么关系？积的绝对值呢？
21 -21 -21 21 0 0
一般地，我们有以下有理数的乘法法则:两数相乘，同号得正，异号得负，并把绝对值相乘。任何数与零相乘，积为零。
想一想几 个 有 理 数 相 乘 ，怎 样 确 定 积 的 符号？
【例2】若一个数的倒数仍是这个数，则这个数是( )或-1
解：倒数是本身的数是1或-1.故选D
【例3】两个互为相反数的有理数相乘，积为( ).A.正数B.负数C.零D.负数或零
两个互为相反数的数有两种情况：一正一负或都为0，所以应选D.
【例4】现有四种说法：①几个有理数相乘，当负因数有奇数个时，积为负；②几个有理数相乘，积为负时，负因数有奇数个；③当x<0时,|x|=-x;④当|x|=-x时，x<0.其中正确的说法是( )A.②③ B.③④ C.②③④ D.①②③④
解：①几个有理数相乘，只要有一个因数为0，不管负因数有奇数个还是偶数个，积都为0，而不会是负数，错误;②正确;③正确;④当|x|=-x时，x≤0，错误.故选：A.
-2 -1 0 1
c b a
一般地，我们有以下有理数的乘法法则:两数相乘，同号得正，异号得负，并把绝对值相乘。任何数与零相乘，积为零。有多个不为0的有理数相乘时，可以先确定积的符号，再将绝对值相乘。若两个有理数的乘积为1，就称这两个有理数互为倒数。0没有倒数。
【必做】2.下列结论正确的是( )A.若a<0,b>0,则ab>0B.若a>0,b<0，则ab<0C.若a<0,b<0，则ab<0D.若a>0,b>0，则ab<0
【必做】3.绝对值不大于4的整数的积是( )负数或0D.-1
绝对值不大于4的整数有0，±1，±2，±3，±4，任何数与零相乘，积为0. 故选B
【必做】4.商店降价销售某种商品，每件降价5元，售出60件后，与原价销售同样数量的商品相比，销售额变化情况的算式表示为( )A.(-5)×60C.5×(-60)B.5×60D.(-5)×(-60)
【选做】5.若a,b互为相反数，c,d互为倒数，m的绝对值是1，求(a+b)cd-2024m的值。
a,b互为相反数，则a+b=0，c,d互为倒数，则cd=1，m的绝对值是1，m为±1，当m=+1,(a+b)cd-2024m=0+2024=2024当m=-1,(a+b)cd-2024m=0+(-2024)=-2024
【选做】6.已知a，b，c在数轴上的位置如图所示，有下列结论:①b+c＞0；②abc＞0；③b﹣c＜0；④(b+c)(b﹣c)，其中正确结论的个数是(　)A．1B．2C．3D．4
a c 0 b
【选做】6.解：由a，b，c在数轴上的位置可知，a|a|>|c|,∴①b+c>0，故正确;②abc>0，故正确；③b-c>0，故错误;④(b+c)(b-c)>0，故正确故选：C.
【拓展题】【阅读】我们学习了有理数的加法法则与有理数的乘法法则.在学习此内容时，掌握了法则，同时也学会了分类思考.【探索】(1)若ab=6,则a+b的值为①正数，②负数,③0.你认为结果可能是_____.(填序号)(2)若a+b=-5,且a,b为整数，则ab的最大值为_____【拓展】(3)数轴上A，B两点分别对应有理数ab，若ab<0，试比较a+b与0的大小.
【拓展题】解:(1)①②ab可能同号也可能异号(2)6若ab有最大值，则积为正，故ab同号，又知a+b=-5，∴a,b为-2，-3 ∴ab最大值为6