

四川省达州铁路中学2023-2024学年八年级下学期期中检测数学试卷
展开1.下列手机中的图标是中心对称图形的是( )
A.B.C.D.
2.若a<b,则下列结论不一定成立的是( )
A.a﹣1<b﹣1B.a2<b2C.a3
A.2,4B.-6,4C.1,-3D.-5,5
4.下列等式从左到右的变形,属于因式分解的是( )
A.4x2+y2=2x+y2x-y B.a4-y=4a-ay2
C.x2+3x-1=xx+3-1 D.-4x+12xy-9y2=-2x-3y2
5.下图是一个不等式组中的所有不等式的解集在数轴上的表示,则该不等式组的解集是( )
A.x>-1B.-1
A.11B.13C.11或13D.11或15
7.一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三边的距离相等,凉亭的位置应选在( )
A.三角形三条边的垂直平分线的交点B.三角形三条角平分线的交点
C.三角形三条高所在直线的交点D.三角形三条中线的交点
8.如图,将△ABC绕点C顺时针旋转,点A的对应点为点E,点B的对应点为点D,当旋转角为90°,A,D,E三点在同一直线上时,则∠E的度数为( )
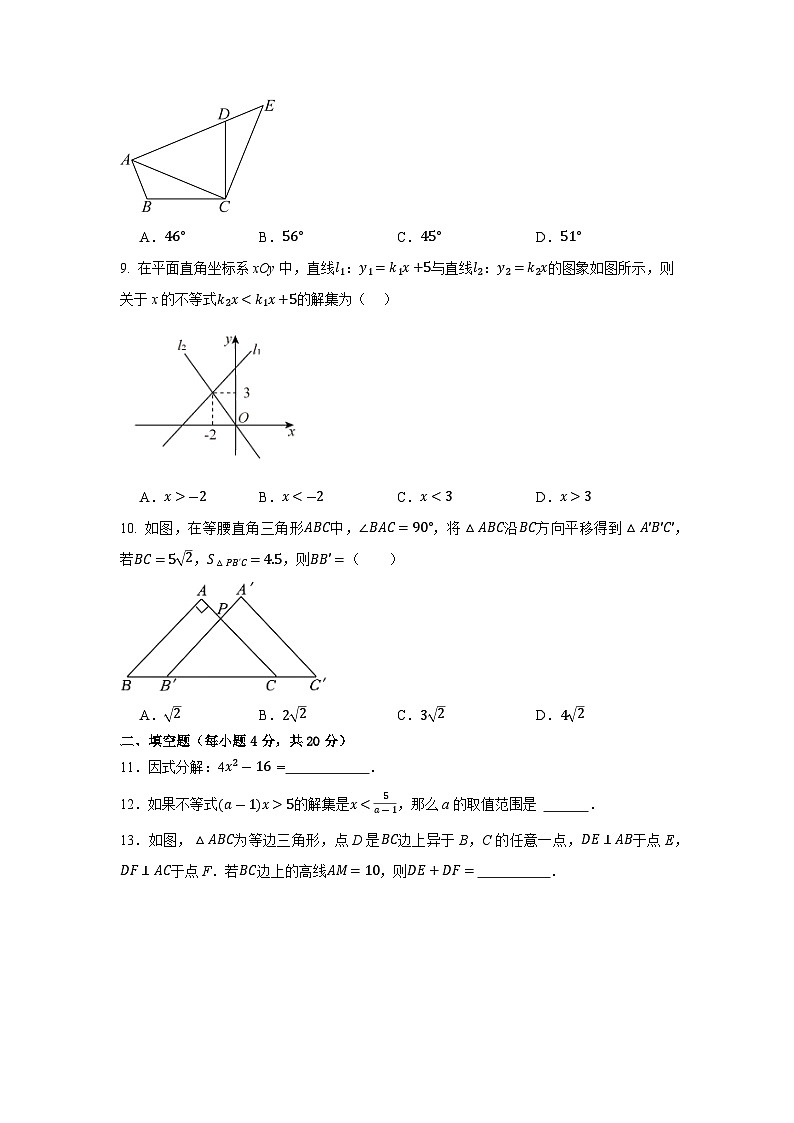
A.46°B.56°C.45°D.51°
在平面直角坐标系xOy中,直线l1:y1=k1x+5与直线l2:y2=k2x的图象如图所示,则关于x的不等式k2x
x>-2B.x<-2C.x<3D.x>3
如图,在等腰直角三角形ABC中,∠BAC=90°,将△ABC沿BC方向平移得到△A'B'C',若BC=52,S△PB'C=4.5,则BB'=( )
A.2B.22C.32D.42
二、填空题(每小题4分,共20分)
11.因式分解:4x2-16 = .
12.如果不等式a-1x>5的解集是x<5a-1,那么a的取值范围是 .
13.如图,△ABC为等边三角形,点D是BC边上异于B,C的任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC边上的高线AM=10,则DE+DF= .
如图,在△ABC中,分别以点A和点C为圆心,大于12AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=2,△ABD的周长为11,则△ABC的周长为 .
15.如图,△ABC中,∠ABC的角平分线BD和AC边的中垂线DE交于点D,DM⊥BA的延长线于点M,DN⊥BC于点N.若AB=3,BC=7,则AM的长为 .
三、解答题(共90分)
16. (1)(4分)解不等式:10+3x+2≤x-2
(2)(6分)解不等式组:4+3x<13x+23-x≤2
17.(5分)因式分解:a3+ab2﹣2a2b
18.(9分)如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.请你画出以下图形:
(1)将△ABC向下平移4个单位,得到的△A′B′C′;
(2)将△A′B′C′绕点C'顺时针旋转90°,得到的△A″B″C′;
(3)以点AA′A″为顶点的三角形的面积为 .
(8分)如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
(9分)先阅读下面的内容,再解决问题:
对于形如这样的二次三项式,可以用公式法将它分解成的形式.但对于二次三项式,就不能直接运用公式了.此时,我们可以在二次三项式x2+中先加上一项,使它与的和成为一个完全平方式,再减去,于是有:
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.利用“配方法”,解决下列问题:
(1)分解因式:
(2)已知、、是的三边,且满足,试判断的形状.
(3)当为何值时代数式有最大值?求出这个最大值.
21. (9分)计算:
(1)1﹣= ;
(2)(1﹣)(1﹣)= ;
(3)(1﹣)(1﹣)(1﹣)= ;
(4)请你利用你找到的简便方法计算:
(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
22.(10分)【初步探究】
(1)如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE、DE.判断△AED的形状,并说明理由.
【拓展应用】
(2)如图2,在平面直角坐标系xOy中,已知点A1,0,点B4,1,点C在第四象限内,若△ABC是等腰直角三角形,则点C的坐标是 .
(3)如图3,在平面直角坐标系xOy中,已知点A2,0,点C是y轴上的动点,线段CA绕若点C按逆时针方向旋转至线段CB,CA=CB,连接BO、BA,则BO+BA的最小值是 .
23.(8分)达州铁路中学组织七年级、八年级学生和带队老师共700人参加研学活动,已知学生人数的一半比带队老师人数的10倍还多35人.
(1)参加活动的八年级学生和带队老师各有多少人?
(2)某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示;
学校计划租用A、B两种型号的客车共16辆接送八年级师生,若每天租车的总费用不超过16200元.共有几种不同的租车方案?最少的租车费用为多少元?
24.(11分)如图1,直线AB:y=2x+2与直线AC交于y轴上一点A,点C在x轴正半轴上,OC=32.
(1)求直线AC的函数表达式;
(2)如图2,将直线AC绕点C逆时针旋转与射线AB交于点D,若△ACD面积是154,求点D的坐标;
(3)点E是直线AC上的一个动点,在坐标轴上找一点F,连接BE,EF,FB,当△BEF是以EF为底边的等腰直角三角形时,直接写出F点的坐标.
25.(11分)请阅读材料并填空:
如图1,在等边三角形ABC内有一点P,且PA=2,PB=3,PC=1.求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:
将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2).连接PP'.
(1)根据李明同学的思路,进一步思考后可求得∠BPC= °,等边△ABC的边长为 .
(2)请你参考李明同学的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA= 5,BP= 2,PC=1.求∠BPC的度数和正方形ABCD的边长.
(3)【实际应用】图4所示是一个三角形公园,其中顶点A,B,C为公园的出入口,∠A=75°,AB=22km,AC=4km,工人师傅准备在公园内修建一凉亭P,使该凉亭到三个出入口的距离最小,则PA+PB+PC的最小值是__ ____km.
A型号客车
B型号客车
载客量(人辆)
40
55
租金(元/辆)
900
1200
参考答案:
一、选择:1-5 BBBDC 6-10 CBCAB
二、填空:11.4(x+2)(x-2) 12. a<1 13. 10 14. 15 15. 2
三、解答题16.解:(1)10+3x+2≤x-2,
去括号得:10+3x+6≤x-2,
移项得:3x-x≤-2-10-6,
合并同类项得:2x≤-18,
系数化为1得:x≤-9;
(2)4+3x<13①x+23-x≤2②
解不等式①得:x<3,
解不等式②得:x>-2,
∴不等式组的解集为-2≤x<3.
17.aa-b2
【分析】先提取公因式a,再利用完全平方公式继续分解即可.
【详解】a3﹣2a2b+ab2
=a(a2-2ab+b2)
=a(a-b)2.
18.解:(1)如图所示 (2)如图所示
(3)8
19.(1)证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中
∴Rt△ACD≌Rt△AED(HL);
(2)解:∵DC=DE=1,DE⊥AB,
∴∠DEB=90°,
∵∠B=30°,
∴BD=2DE=2.
(1)(a-4)(a-2)
(2)解:∵a2c2-b2c2=a4-b4,
∴a2-b2c2=a2-b2a2+b2,
∴a2-b2a2+b2-c2=0
∴a2-b2=0或a2+b2-c2=0,
解得a=b或a2+b2=c2,
∴△ABC是等腰三角形或直角三角形.
(3)-x2-4x+8
=-x2+4x-8
=-x2+4x+4-12
=-(x+2)2+12
∴x+2=0,解得x=-2,原式有最大值=12
21.解:(1) (2) (3)
(4)请你利用你找到的简便方法计算:
(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣)
=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)
=××××××…××××
=.
22.(1)结论:△AED是等腰直角三角形.
理由:∵在△ABE和△ECD中,
AB=CE∠B=∠C=90°BE=CD,
∴△ABE≌△ECDSAS,
∴AE=DE,∠AEB=∠EDC,
∵在Rt△EDC中,∠C=90°,
∴∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∵∠AEB+∠DEC+∠AED=180°,
∴∠AED=90°,
∴△AED是等腰直角三角形;
2,-3或5,-2或3,-1
(3)25.
23.(1)解:设带队老师有x人,则学生有210x+35人,
由题意可得:x+210x+35=700,
解得:x=30,
∴210x+35=2×10×30+35=670,
答:参加活动的八年级学生有670人,老师有30人;
(2)解:设租用A种型号的客车a辆,则租用B种型号的客车16-a辆,总费用为w元,
由题意可得:w=900a+120016-a=-300a+19200,
∵w=-300<0,
∴w随a的增大而减小,
∵每天租车的总费用不超过16200元,学校组织八年级学生和带队老师共700人参加研学活动,
∴-300a+19200≤1620040a+5516-a≥700,
解得:10≤a≤12,
∵a为整数,
∴a=10或11或12,即共有三种租车方案,
∴当a=12时,w取得最小值,此时w=15600,
答:共有三种不同的租车方案,最少的租车费用为15600元.
24.(1)解:∵直线AB:y=2x+2分别与x轴,y轴交于B、A两点,
∴在y=2x+2中,当x=0时,y=2,
∴A点坐标为0,2,
∵点C在x轴正半轴上,OC=32,
∴C32,0,
设直线AC的解析式为y=kx+b,
∴32k+b=0b=2,
∴k=-43b=2,
∴直线AC的函数表达式为y=-43x+2;
(2)解:∵直线AB:y=2x+2分别与x轴,y轴交于B、A两点,
∴在y=2x+2中,当y=0时,2x+2=0,
解得x=-1,
∴B-1,0,
∴OB=1,
∴BC=1+32=52,
∵A0,2,
∴OA=2,
∴S△ABC=12BC⋅AO=12×52×2=52,
由题意知,点D在x轴下方,
∵S△ACD=S△ABC+S△BCD,
∴52+12×52×yD=154,
∴yD=-1,
把y=-1代入y=2x+2,
∴2x+2=-1,
解得x=-32,
∴D-32,-1;
点F的坐标为73,0或-133,0或0,-74或0,134.
(1)150, 7
(2)如图,
将△BPC绕点B逆时针旋转90°,得△BP'A,则△BPC≌△BP'A.
∴AP'=PC=1,BP=BP'=2;
连接PP',在Rt△BP'P中,
∵BP=BP'=2,∠PBP'=90°,
∴PP'=2,∠BP'P=45°;
在△AP'P中,AP'=1,PP'=2,AP=5,
∵12+22=52,即AP'2+PP'2=AP2;
∴△AP'P是直角三角形,即∠AP'P=90°,
∴∠AP'B=135°,
∴∠BPC=∠AP'B=135°.
过点B作BE⊥AP',交AP'的延长线于点E;则△BEP'是等腰直角三角形,
∴∠EP'B=45°,
∴EP'=BE=1,
∴AE=2;
∴在Rt△ABE中,由勾股定理,得AB=5;
∴∠BPC=135°,正方形边长为5.
(3)210
2023-2024学年四川省成都市金牛区铁路中学八年级(下)期中数学试卷(含解析): 这是一份2023-2024学年四川省成都市金牛区铁路中学八年级(下)期中数学试卷(含解析),共24页。试卷主要包含了选择题,非选择题等内容,欢迎下载使用。
四川省达州市渠县中学2022—2023学年下学期八年级期中数学试卷: 这是一份四川省达州市渠县中学2022—2023学年下学期八年级期中数学试卷,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省达州市通川区铁路中学七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年四川省达州市通川区铁路中学七年级(下)期末数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












