2024-2025学年铜川市重点中学数学九年级第一学期开学质量检测模拟试题【含答案】

这是一份2024-2025学年铜川市重点中学数学九年级第一学期开学质量检测模拟试题【含答案】，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）利用反证法证明命题“在中，若，则”时，应假设
A．若，则B．若，则
C．若，则D．若，则
2、（4分）如图，正方形ABCD中，AB=6，点E在边CD上，且CD=1DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S△FGC=1．其中正确结论的个数是（ ）
A．1B．2C．1D．4
3、（4分）点P（﹣3，m+1）在第二象限，则m的取值范围在数轴上表示正确的是（ ）
A．B．
C．D．
4、（4分）已知△ABC的三边长分别为10，24，26，则最长边上的中线长为（ ）
A．14B．13C．12D．11
5、（4分）使用同一种规格的下列地砖，不能进行平面镶嵌的是（ ）
A．正三角形地砖 B．正四边形地砖 C．正五边形地砖 D．正六边形地砖
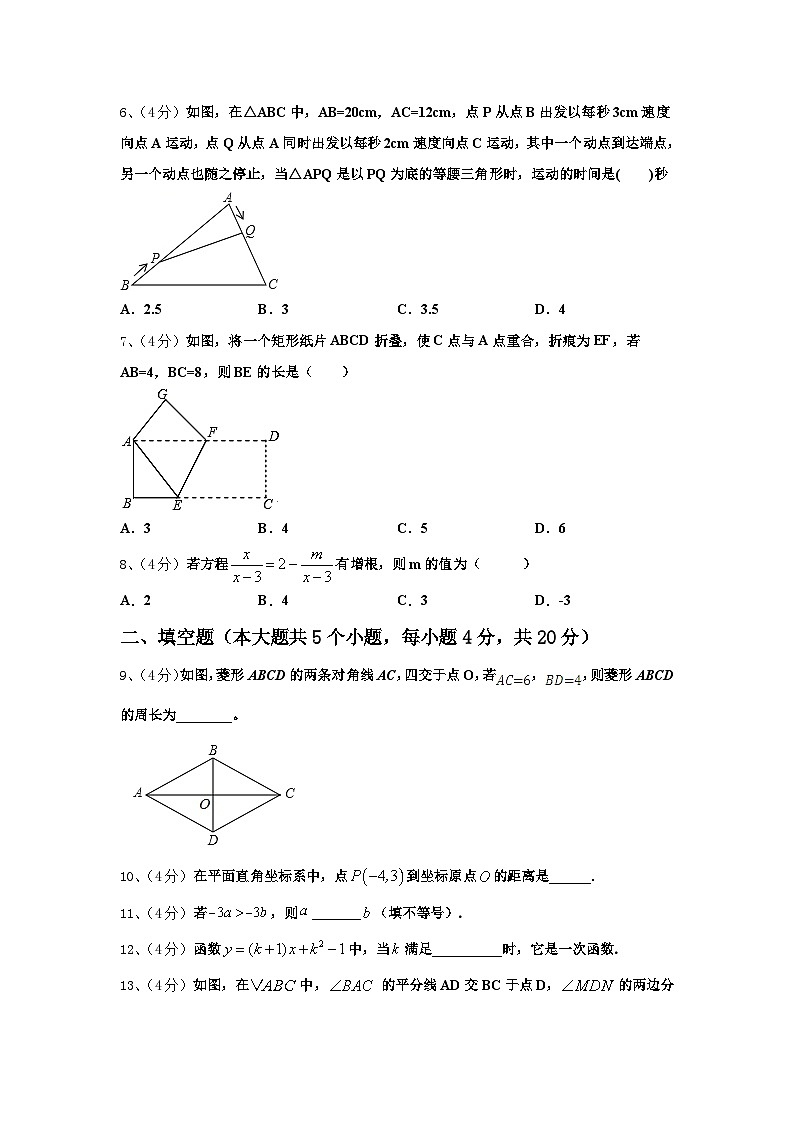
6、（4分）如图，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm速度向点A运动，点Q从点A同时出发以每秒2cm速度向点C运动，其中一个动点到达端点，另一个动点也随之停止，当△APQ是以PQ为底的等腰三角形时，运动的时间是( )秒
A．2.5B．3C．3.5D．4
7、（4分）如图，将一个矩形纸片ABCD折叠，使C点与A点重合，折痕为EF，若AB=4，BC=8，则BE的长是（ ）
A．3B．4C．5D．6
8、（4分）若方程有增根，则m的值为（ ）
A．2B．4C．3D．-3
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，菱形ABCD的两条对角线AC，四交于点O，若，，则菱形ABCD的周长为________。
10、（4分）在平面直角坐标系中，点到坐标原点的距离是______.
11、（4分）若，则_______（填不等号）.
12、（4分）函数中，当满足__________时，它是一次函数.
13、（4分）如图，在中，的平分线AD交BC于点D，的两边分别与AB、AC相交于M、N两点，且，若，则四边形AMDN的面积为___________.
三、解答题（本大题共5个小题，共48分）
14、（12分）杨梅是漳州的特色时令水果.杨梅一上市，水果店的老板用1200元购进一批杨梅，很快售完；老板又用2500元购进第二批杨梅，所购件数是第一批的2倍，但进价每件比第一批多了5元.
（1）第一批杨梅每件进价多少元？
（2）老板以每件150元的价格销售第二批杨梅，售出后，为了尽快售完，决定打折促销.要使得第二批杨梅的销售利润不少于320元，剩余的杨梅每件售价至少打几折（利润售价进价）？
15、（8分）如图，已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数；
(2)若AB=10,BC=12,求△ABD的周长.
16、（8分）分解因式：2x2﹣12x+1．
17、（10分）随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业，据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座。
（1）计划到2020年底，全省5G基站的数量是多少万座？；
（2）按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率。
18、（10分）如图，一架5米长的梯子AB斜靠在一面墙上，梯子底端B到墙底的垂直距离BC为3米．
（1）求这个梯子的顶端A到地面的距离AC的值；
（2）如果梯子的顶端A沿墙AC竖直下滑1米到点D处，求梯子的底端B在水平方向滑动了多少米？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若x=3是分式方程的根，则a的值是__________．
20、（4分）如图所示，折叠矩形的一边 AD，使点 D 落在边 BC 的点 F处，已知 AB=8cm，BC=10cm，则 EC 的长为_____cm．
21、（4分）如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若BD=2，CD=1，则AC的长是_______．
22、（4分）已知，则__________．
23、（4分）点A（-1，y1），B（2，y2）均在直线y=-2x+b的图象上，则y1___________y2（选填“＞”＜”=”）
二、解答题（本大题共3个小题，共30分）
24、（8分）某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同.
（1）a=__，=____；
（2）①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析，谁将被选中.
25、（10分）阅读下列材料：
关于x的方程：的解是，；即的解是；的解是，；的解是，；
请观察上述方程与解的特征，比较关于x的方程与它们的关系，猜想它的解是什么？并利用“方程的解”的概念进行验证．
由上述的观察、比较、猜想、验证，可以得出结论：
如果方程的左边是未知数与其倒数的倍数的和，方程的右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解，请用这个结论解关于x的方程：．
26、（12分）先化简，再求值： [其中，]
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
反证法的步骤中，第一步是假设结论不成立，反面成立，据此进行解答．
【详解】
解：用反证法证明命题“在中，若，则”时，应假设若，则，
故选：．
本题考查的是反证法，解此题关键要懂得反证法的意义及步骤．在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
2、C
【解析】
根据正方形基本性质和相似三角形性质进行分析即可.
【详解】
①正确．因为AB=AD=AF，AG=AG，∠B=∠AFG=90°，∴△ABG≌△AFG；
②正确．因为：EF=DE=CD=2，设BG=FG=x，则CG=6﹣x．在直角△ECG中，根据勾股定理，得（6﹣x）2+42=（x+2）2，解得x=1．所以BG=1=6﹣1=GC；
③正确．因为CG=BG=GF，所以△FGC是等腰三角形，∠GFC=∠GCF．又∠AGB=∠AGF，∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF，
∴∠AGB=∠AGF=∠GFC=∠GCF，∴AG∥CF；
④错误．
过F作FH⊥DC，
∵BC⊥DH，
∴FH∥GC，
∴△EFH∽△EGC，
∴
EF=DE=2，GF=1，
∴EG=5，
∴
∴S△FGC=S△GCE﹣S△FEC=
故选C．
考核知识点：相似三角形性质.
3、C
【解析】
由第二象限纵坐标大于零得出关于m的不等式，解之可得．
【详解】
解：由题意知m+1＞0，
解得m＞﹣1，
故选：C．
本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
4、B
【解析】
根据勾股定理的逆定理可判定△ABC是直角三角形，从而可根据斜边上的中线是斜边上的中线是斜边的一半求解．
【详解】
∵102+242=262，
∴△ABC是直角三角形，
∵直角三角形中最长的边即斜边为26，
∴最长边上的中线长=1．
故选B．
此题主要考查学生对勾股定理的逆定理及直角三角形斜边上的中线的综合运用能力．
5、C
【解析】试题解析：A、正三角形的每个内角是60°，能整除360°，能密铺，故A不符合题意；
B、正四边形每个内角是90°，能整除360°，能密铺，故B不符合题意；
C、正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能密铺，故C符合题意；
D、正六边形每个内角是120°，能整除360°，能密铺，故D不符合题意．
故选C．
6、D
【解析】
解：设运动的时间为x，
在△ABC中，AB=20cm，AC=12cm，
点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，
当△APQ是等腰三角形时，AP=AQ，AP=20﹣3x，AQ=2x，即20﹣3x=2x，
解得x=1．
故选D．
此题主要考查学生对等腰三角形的性质这一知识点的理解和掌握，此题涉及到动点，有一定的拔高难度，属于中档题．
7、A
【解析】
分析：根据翻折变换的性质可得AE=CE，设BE=x，表示出AE，然后在Rt△ABE中，利用勾股定理列方程求解即可．
详解：∵矩形纸片ABCD折叠C点与A点重合，
∴AE=CE，
设BE=x，则AE=8−x，
在Rt△ABE中,由勾股定理得,AB2+BE2=AE2，
即42+x2=(8−x)2，
解得x=3，
即BE=3.
故选A.
点睛：本题考查了翻折变换的性质，主要利用了翻折前后对应线段相等，难点在于利用勾股定理列出方程.
8、D
【解析】
增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母（x−1）＝0，得到x＝1，然后代入化为整式方程的方程算出m的值．
【详解】
方程两边都乘（x−1），
得x=2（x−1）-m，
∵原方程有增根，
∴最简公分母（x−1）＝0，
解得x＝1，
当x＝1时，1=2（1−1）-m
m＝-1．
故选：D．
本题考查了分式方程的增根，增根问题可按如下步骤进行：
①让最简公分母为0确定增根；
②化分式方程为整式方程；
③把增根代入整式方程即可求得相关字母的值．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
首先根据菱形的性质可知菱形的对角线垂直平分，然后在Rt△AOD中利用勾股定理求出AD的长，再由菱形的四边形相等，可得菱形ABCD的周长．
【详解】
∵四边形ABCD是菱形，
∴AC⊥BD，AO=AC=3，DO=BD=2，
在Rt△AOD中，AD=，
∴菱形ABCD的周长为4．
故答案为：4．
本题考查了菱形的性质以及勾股定理的知识，解答本题的关键是掌握菱形的对角线互相垂直且平分以及勾股定理等知识．
10、5
【解析】
根据勾股定理解答即可．
【详解】
点P到原点O距离是．
故答案为：5
此题考查勾股定理，关键是根据勾股定理得出距离．
11、<
【解析】
试题分析：根据不等式的基本性质3，直接求解得a＜b.
故答案为＜
12、k≠﹣1
【解析】
分析: 根据一次函数的定义解答即可，一般地，形如y=kx+b,（k为常数，k≠0）的函数叫做一次函数.
详解:由题意得，
k+1≠0,
∴k ≠-1.
故答案为k ≠-1.
点睛: 本题考查了一次函数的定义，熟练掌握一次函数的定义是解答本题的关键.
13、9 ．
【解析】
作DE⊥AB于点E，DF⊥AC于点F，依据HL判定Rt△ADE≌Rt△ADF，即可得出AE=AF；判定△DEM≌△DFN，可得S△DEM=S△DFN，进而得到S四边形AMDN=S四边形AEDF，求得S△ADF=AF×DF= ，即可得出结论．
【详解】
解：作DE⊥AB于点E，DF⊥AC于点F，
∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，
∴DE=DF，
又∵DE⊥AB于点E，DF⊥AC于点F，
∴∠AED=∠AFD=90°，
又∵AD=AD，
∴Rt△ADE≌Rt△ADF（HL），
∴AE=AF；
∵∠MDN+∠BAC=180°，
∴∠AMD+∠AND=180°，
又∵∠DNF+∠AND=180°
∴∠EMD=∠FND，
又∵∠DEM=∠DFN，DE=DF，
∴△DEM≌△DFN，
∴S△DEM=S△DFN，
∴S四边形AMDN=S四边形AEDF，
∵，AD平分∠BAC，
∴∠DAF=30°，
∴Rt△ADF中，DF=3，AF= =3 ，
∴S△ADF= AF×DF=×3×3= ，
∴S四边形AMDN=S四边形AEDF=2×S△ADF=9 ．
故答案为9 ．
本题考查全等三角形的性质和判定、角平分线的性质定理等知识；熟练掌握全等三角形的判定与性质是解决问题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）120元（2）至少打7折．
【解析】
（1）设第一批杨梅每件进价是x元，则第二批每件进价是（x+5）元，再根据等量关系：第二批杨梅所购件数是第一批的2倍；
（2）设剩余的杨梅每件售价y元，由利润=售价-进价，根据第二批的销售利润不低于320元，可列不等式求解．
【详解】
解：(1)设第一批杨梅每件进价是x元，
则
解得
经检验，x=120是原方程的解且符合题意．
答：第一批杨梅每件进价为120元．
(2)设剩余的杨梅每件售价打y折．
则
解得y≥7.
答：剩余的杨梅每件售价至少打7折．
考查分式方程的应用, 一元一次不等式的应用，读懂题目，从题目中找出等量关系以及不等关系是解题的关键.
15、（1）20°；（2）22.
【解析】
试题分析：（1）根据三角形内角和定理求出∠C，根据线段垂直平分线的性质得到DA=DC，求出∠DAC，计算即可；
（2）根据DA=DC，三角形的周长公式计算．
解：(1)∵∠BAC=60°,∠B=80°,
∴∠C=180°-∠BAC-∠B=180°-60°-80°=40°,
∵DE垂直平分AC,∴DA=DC.
∴∠DAC=∠C=40°,
∴∠BAD=60°-40°=20°.
（2）∵DE垂直平分AC,
∴AD=CD,
∴AB+AD+BD=AB+CD+BD=AB+BC=10+12=22，
∴△ABD的周长为22.
16、2(x﹣3)2．
【解析】
原式提取公因式后，利用完全平方公式分解即可．
【详解】
原式＝2(x2﹣6x+9)
＝2(x﹣3)2．
此题考查了提公因式与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
17、（1）到2020年底，全省5G基站的数量是6万座；（2）2020年底到2022年底，全省5G基站数量的年平均增长率为.
【解析】
（1）2020年全省5G基站的数量=目前广东5G基站的数量×4，即可求出结论；
（2）设2020年底到2022年底，全省5G基站数量的年平均增长率为x，根据2020年底及2022年底全省5G基站数量，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
【详解】
解：（1）由题意可得：到2020年底，全省5G基站的数量是（万座）.
答：到2020年底，全省5G基站的数量是6万座.
（2）设年平均增长率为，由题意可得：
，
解得：，（不符合，舍去）
答：2020年底到2022年底，全省5G基站数量的年平均增长率为.
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
18、（1）4（2）1
【解析】
（1）在直角三角形ABC中，利用勾股定理即可求出AC的长；
（2）首先求出CD的长，利用勾股定理可求出CE的长，进而得到BE=CE-CB的值．
【详解】
（1）在Rt△ABC中，由勾股定理得AC2+CB2=AB2，
即AC2+32=52，
所以AC=4（m），
即这个梯子的顶端A到地面的距离AC为4m；
（2）DC=4-1=3（m），DE=5=m，
在Rt△DCE中，由勾股定理得DC2+CE2=DE2，
即32+CE2=52，
所以CE=5（m），
BE=CE-CB=4-3=1（m），
即梯子的底端B在水平方向滑动了1m．
本题考查了勾股定理在实际生活中的应用，本题中根据梯子长不会变这一关系进行求解是解题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
首先根据题意，把x=1代入分式方程，然后根据一元一次方程的解法，求出a的值是多少即可．
【详解】
解：∵x=1是分式方程的根，
∴，
∴＝0，
∴a-1=0，
∴a=1，
即a的值是1
故答案为：1．
此题主要考查了分式方程的解，要熟练掌握，解答此题的关键是要明确：在解方程的过程中因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根，增根是令分母等于0的值，不是原分式方程的解．此题还考查了一元一次方程的求解方法，要熟练掌握．
20、2
【解析】
试题解析：∵D，F关于AE对称，所以△AED和△AEF全等，
∴AF=AD=BC=10，DE=EF，
设EC=x，则DE=8-x．
∴EF=8-x，
在Rt△ABF中，BF==6，
∴FC=BC-BF=1．
在Rt△CEF中，由勾股定理得：CE2+FC2=EF2，
即：x2+12=（8-x）2，解得x=2．
∴EC的长为2cm．
考点：1.勾股定理；2.翻折变换（折叠问题）．
21、
【解析】
作DE⊥AB于E，根据角平分线的性质得到DE=DC，根据勾股定理求出BE，再根据勾股定理计算即可．
【详解】
解：作DE⊥AB于E，
∵AD是∠BAC的平分线，∠ACB=90°，DE⊥AB，
∴DE=DC=1，
在Rt△ACD和Rt△AED中，
∴Rt△ACD≌Rt△AED（HL），
∴AC=AE，
由勾股定理得，
设AC=AE=x，
由勾股定理得x2+32=（x+）2，
解得x=．
∴AC=．
故答案为：．
本题考查的是勾股定理以及角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
22、1
【解析】
直接利用二次根式非负性得出a，b的值，进而得出答案．
【详解】
∵，
∴a＝−1，b＝1，
∴−1＋1＝1．
故答案为：1．
此题主要考查了非负数的性质，正确得出a，b的值是解题关键．
23、＞．
【解析】
函数解析式y=-2x+b知k＜0，可得y随x的增大而减小，即可求解．
【详解】
y=-2x+b中k＜0，
∴y随x的增大而减小，
∵-1＜2，
∴y1＞y2，
故答案为＞．
本题考查一次函数的图象及性质；熟练掌握一次函数的图象及性质是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）4，6；（2）乙
【解析】
（1）根据总成绩相同可求得a;
（2）根据方差公式，分别求两者方差.即s²=[(x1-)²+(x2-)²+...+(xn-)²]；因为两人成绩的平均水平（平均数）相同，所以从方差得出乙的成绩比甲稳定.
【详解】
（1）由题意得：甲的总成绩是：9+4+7+4+6=30，则a=30﹣7﹣7﹣5﹣7=4， ═30÷5=6；
（2）甲的方差为：[（9﹣6）2+（4﹣6）2+（7﹣6）2+（4﹣6）2+（6﹣6）2]=3.6.
乙的方差为： [（7﹣6）2+（5﹣6）2+（7﹣6）2+（4﹣6）2+（7﹣6）2]=1.6.
②因为两人成绩的平均水平（平均数）相同，根据方差得出乙的成绩比甲稳定，所以乙将被选中；
本题考核知识点：平均数，方差.解题关键点：理解平均数和方差的意义.
25、猜想的解是，．验证见解析；，．
【解析】
此题为阅读分析题，解此题要注意认真审题，找到规律：的解为，．据规律解题即可．
【详解】
猜想的解是，．
验证：当时，方程左边，方程右边，
方程成立；
当时，方程左边，方程右边，
方程成立；
的解是，；
由得，
，，
，．
考查解分式方程，通过观察，比较，猜想，验证，可以得出结论.解决此题的关键是理解题意，认真审题，寻找规律.
26、
【解析】
分析：先化简，再把代入化简后的式子进行运算即可.
详解：
，
当x=时，
原式=
点睛：本题考查了分式的化简求值.
题号
一
二
三
四
五
总分
得分
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7