2024-2025学年陕西省渭南市合阳县九年级数学第一学期开学统考模拟试题【含答案】

这是一份2024-2025学年陕西省渭南市合阳县九年级数学第一学期开学统考模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
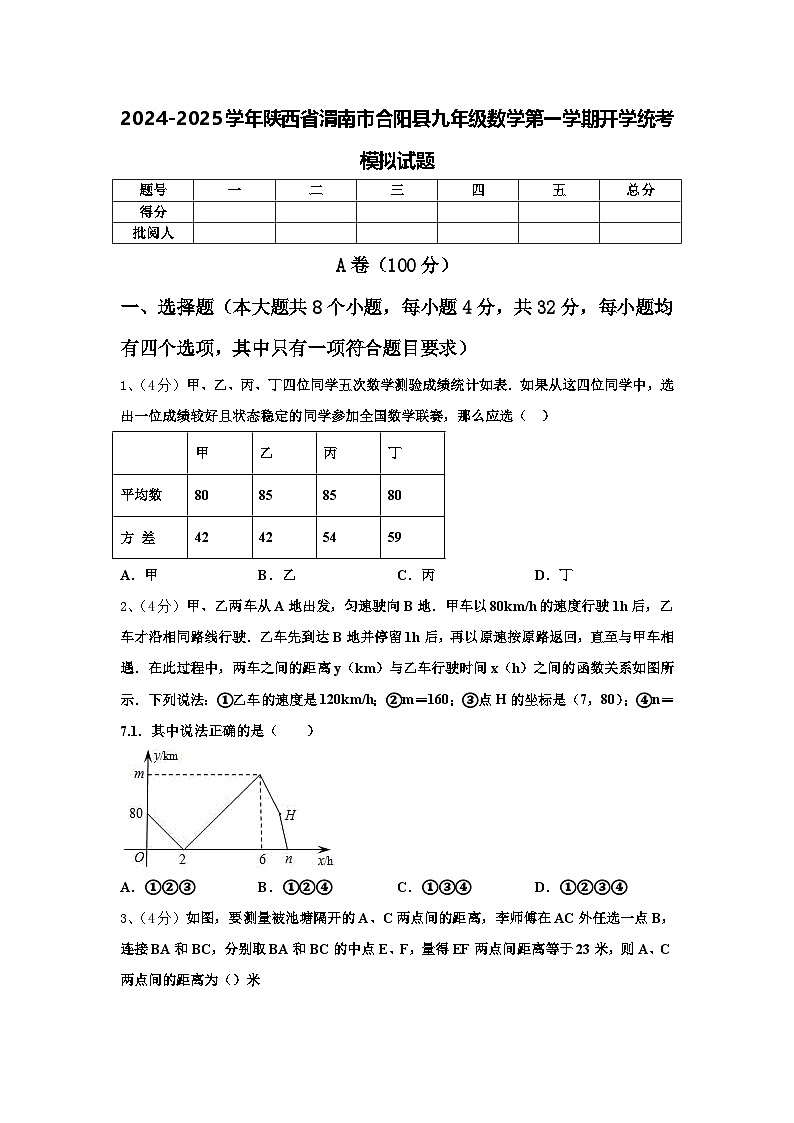
1、（4分）甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加全国数学联赛，那么应选（ ）
A．甲B．乙C．丙D．丁
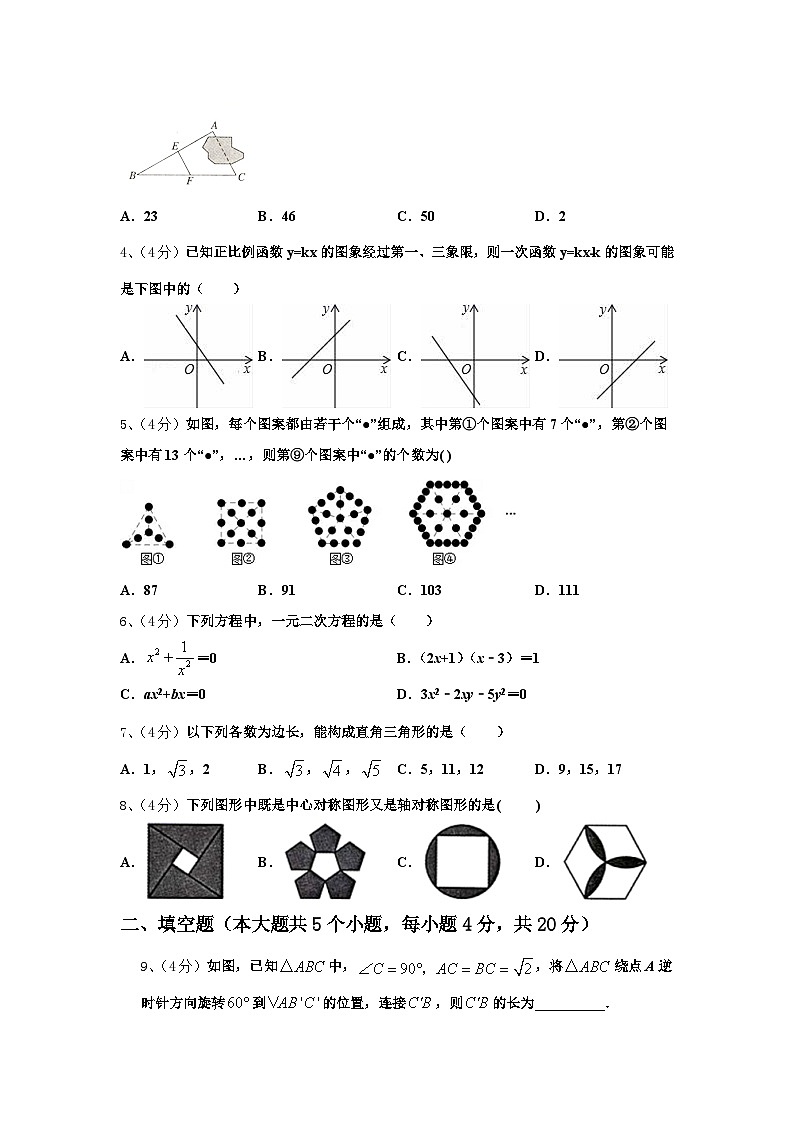
2、（4分）甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.1．其中说法正确的是（ ）
A．①②③B．①②④C．①③④D．①②③④
3、（4分）如图，要测量被池塘隔开的A、C两点间的距离，李师傅在AC外任选一点B，连接BA和BC，分别取BA和BC的中点E、F，量得EF两点间距离等于23米，则A、C两点间的距离为（）米
A．23B．46C．50D．2
4、（4分）已知正比例函数y=kx的图象经过第一、三象限，则一次函数y=kx﹣k的图象可能是下图中的（ ）
A．B．C．D．
5、（4分）如图，每个图案都由若干个“●”组成，其中第①个图案中有7个“●”，第②个图案中有13个“●”，…，则第⑨个图案中“●”的个数为( )
A．87B．91C．103D．111
6、（4分）下列方程中，一元二次方程的是（ ）
A．＝0B．（2x+1）（x﹣3）＝1
C．ax2+bx＝0D．3x2﹣2xy﹣5y2＝0
7、（4分）以下列各数为边长，能构成直角三角形的是（ ）
A．1，，2B．，，C．5，11，12D．9，15，17
8、（4分）下列图形中既是中心对称图形又是轴对称图形的是( )
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，已知中，，将绕点A逆时针方向旋转到的位置，连接，则的长为__________．
10、（4分）某班同学要测量学校升国旗的旗杆高度，在同一时刻，量得某同学的身高是1.5米，影长是1米，且旗杆的影长为8米，则旗杆的高度是 _________________ 米.
11、（4分）如图，矩形纸片中，已知，，点在边上，沿折叠纸片，使点落在点处，连结，当为直角三角形时，的长为______.
12、（4分）已知直角三角形中，分别以为边作三个正方形，其面积分别为，则__________（填“”，“”或“”）
13、（4分）如图，正比例函数y＝kx与反比例函数y＝的图象有一个交点A（m，3），AB⊥x轴于点B，平移直线y＝kx，使其经过点B，得到直线l，则直线l对应的函数解析式是___．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在中，是的中点，，的延长线相交于点，
（1）求证：；
（2）若，且，求的长.
15、（8分）因式分解：am2﹣6ma+9a．
16、（8分）某市从今年1月l同起调整居民用水价格，每立方米水费上涨20%．小丽家去年12月份的水费是15元，而今年5月的水费则是10元．已知小丽家今年5月的用水量比去年12月的用水量多5m1．求该市今年居民用水的价格．
17、（10分）如图，在平面直角坐标系中，OA=OB=8，OD=1，点C为线段AB的中点
(1)直接写出点C的坐标 ；
(2)求直线CD的解析式；
(3)在平面内是否存在点F，使得以A、C、D、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．
18、（10分）如图，在平行四边形ABCD中，BE平分∠ABC交CD的延长线于点E，作CF⊥BE于F．
(1)求证：BF=EF；
(2)若AB=8，DE=4，求平行四边形ABCD的周长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）在Rt△ABC中，∠C＝90°，若a=6，b=8，则c=________．
20、（4分）如图，在菱形ABCD中，对角线AC与BD相交于点O，AC＝24，BD＝10，DE⊥BC，垂足为点E，则DE＝_______．
21、（4分）在平面直角坐标系中，直线与轴交于点，与反比例函数在第一象限内的图像相交于点，将直线平移后与反比例函数图像在第一象限内交于点，且的面积为18，则平移后的直线解析式为__________．
22、（4分）为了解当地气温变化情况，某研究小组记录了寒假期间连续6天的最高气温，结果如下（单位：℃）：－6，－3，x，2，－1，3，若这组数据的中位数是－1，在下列结论中：①方差是8；②极差是9；③众数是－1；④平均数是－1，其中正确的序号是________.
23、（4分）点A（-1，y1），B（3，y2）是直线y=-4x+3图象上的两点，则y1______y2（填“>”或“<”）.
二、解答题（本大题共3个小题，共30分）
24、（8分）某校开展爱“我容城，创卫同行”的活动，倡议学生利用双休日在浜江公园参加评选活动，为了了解同学们劳动时间，学校随机调查了部分同学劳动的时间，并用得到的数据绘制了不完整的统计图，根据图中信息解答下列问题：
（1）将条形统计图补充完整；
（2）抽查的学生劳动时间的众数为______，中位数为_______；
（3）已知全校学生人数为1200人，请估算该校学生参加义务劳动2小时的有多少人？
25、（10分）在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
步数分组统计表
请根据以上信息解答下列问题：
（1）填空：m= ______ ，n= ______ ；
（2）补全频数发布直方图；
（3）这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组；
（4）若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．
26、（12分）如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子的长为13米，此人以0.5米/秒的速度收绳，6秒后船移动到点的位置，问船向岸边移动了大约多少米？（假设绳子是直的，结果精确到0.1米，参考数据：，）
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
试题分析：乙和丙的平均数较高，甲和乙的方差较小，则选择乙比较合适．故选B.
考点：平均数和方差．
【详解】
请在此输入详解！
2、A
【解析】
根据乙追上甲的时间求出乙的速度可判断①，根据乙由相遇点到达B点所用时间可确定m的值，即可判断②，根据乙休息1h甲所行驶的路程可判断③，由乙返回时，甲乙相距80km，可求出两车相遇的时间即可判断④.
【详解】
由图象可知，乙出发时，甲乙相距80km，2小时后，乙车追上甲．则说明乙每小时比甲快40km，则乙的速度为120km/h．①正确；
由图象第2﹣6小时，乙由相遇点到达B，用时4小时，每小时比甲快40km，则此时甲乙距离4×40=160km，则m=160，②正确；
当乙在B休息1h时，甲前进80km，则H点坐标为（7，80），③正确；
乙返回时，甲乙相距80km，到两车相遇用时80÷（120+80）=0.4小时，则n=6+1+0.4=7.4，④错误．
所以正确的有①②③，
故选A.
本题考查通过分段函数图像解决问题，根据题意明确图像中的信息是解题关键.
3、B
【解析】
先判断出EF是△ABC的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半可得AC＝2EF．
【详解】
解：∵点E、F分别是BA和BC的中点，
∴EF是△ABC的中位线，
∴AC＝2EF＝2×23＝46米．
故选：B．
本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理并准确识图是解题的关键．
4、D
【解析】
根据正比例函数的图象经过第一,三象限可得:, 因此在一次函数中,,根据直线倾斜方向向右上方,直线与y轴的交点在y轴负半轴,画出图象即可求解.
【详解】
根据正比例函数的图象经过第一,三象限可得:
所以,
所以一次函数中,,
所以一次函数图象经过一,三,四象限,
故选D.
本题主要考查一次函数图象象限分布性质,解决本题的关键是要熟练掌握一次函数图象图象的象限分布性质.
5、D
【解析】
根据第①个图案中“●”有：1+3×（0+2）个，第②个图案中“●”有：1+4×（1+2）个，第③个图案中“●”有：1+5×（2+2）个，第④个图案中“●”有：1+6×（3+2）个，据此可得第⑨个图案中“●”的个数．
【详解】
解：∵第①个图案中“●”有：1+3×（0+2）=7个，
第②个图案中“●”有：1+4×（1+2）=13个，
第③个图案中“●”有：1+5×（2+2）=21个，
第④个图案中“●”有：1+6×（3+2）=31个，
…
∴第9个图案中“●”有：1+11×（8+2）=111个，
故选：D．
本题考查规律型：图形的变化，解题的关键是将原图形中的点进行无重叠的划分来计数．
6、B
【解析】
试题分析：根据一元二次方程的定义:
A、x2+=0是分式方程；
B、（2x﹣1）（x+2）=1，即2x2+3x﹣3=0是一元二次方程；
C、ax2+bx=0中a=0时，不是一元二次方程；
D、3x2﹣2xy﹣5y2=0是二元二次方程；
故选B．
考点：一元二次方程的定义
7、A
【解析】
根据勾股定理的逆定理可知，当三角形中三边的关系为：a2+b2=c2时，则三角形为直角三角形．
【详解】
A、12+（）2=22，符合勾股定理的逆定理，能组成直角三角形，故正确；
B、（）2+（）2≠（）2，不符合勾股定理的逆定理，不能组成直角三角形，故错误；
C、52+112≠122，不符合勾股定理的逆定理，不能组成直角三角形，故错误；
D、92+152≠172，不符合勾股定理的逆定理，不能组成直角三角形，故错误．
故选：A．
考查的是勾股定理的逆定理：已知三角形ABC的三边满足：a2+b2=c2时，则三角形ABC是直角三角形．解答时，只需看两较小数的平方和是否等于最大数的平方．
8、C
【解析】
根据轴对称图形与中心对称图形的概念求解．
【详解】
A、不是轴对称图形，是中心对称图形，故本选项错误；
B、是轴对称图形，不是中心对称图形，故本选项错误；
C、是轴对称图形，也是中心对称图形，故本选项正确；
D、是轴对称图形，不是中心对称图形，故本选项错误，
故选C．
本此题考查了轴对称及中心对称图形的判断，解答本题的关键是掌握中心对称图形与轴对称图形的概念.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
连接交于D，中，根据勾股定理得，，根据旋转的性质得：垂直平分为等边三角形，分别求出，根据计算即可.
【详解】
如图，连接交于D，如图，
中，∵，
∴，
∵绕点A逆时针方向旋转到的位置，
∴，
∴垂直平分为等边三角形，
∴，
∴．
故答案为：．
考查等腰直角三角形的性质，等边三角形的判定与性质，旋转的性质等，
10、1．
【解析】
在同一时刻，物体的实际高度和影长成比例，据此列方程即可解答．
【详解】
解：设旗杆高度为x，则
，
解得x=1．
故答案为：1．
本题考查相似三角形的应用，熟知同一时刻物高与影长成正比是解题关键．
11、3或
【解析】
分两种情况：①当∠EFC=90°，先判断出点F在对角线AC上，利用勾股定理求出AC，设BE=x,表示出CE，根据翻折变换的性质得到AF=AB,EF=BE，再根据Rt△CEF利用勾股定理列式求解；②当∠CEF=90°，判断四边形ABEF是正方形，根据正方形的性质即可求解.
【详解】
分两种情况：①当∠EFC=90°，如图1，
∵∠AFE=∠B=90°，∠EFC=90°，
∴点A、F、C共线，
∵矩形ABCD的边AD=4，
∴BC=AD=4，
在Rt△ABC中，AC=
设BE=x，则CE=BC-BE=4-x，
由翻折的性质得AF=AB=3,EF=BE=x，∴CF=AC-AF=5-3=2
在Rt△CEF中，EF2+CF2=CE2，
即x2+22=(4-x)2，
解得x=；
②当∠CEF=90°，如图2
由翻折的性质可知∠AEB=∠AEF=45°，
∴四边形ABEF是正方形，
∴BE=AB=3，
故BE的长为3或
此题主要考查矩形的折叠问题，解题的关键是根据图形进行分类讨论.
12、
【解析】
由勾股定理得出AC2+BC2=AB2，得出S1+S2=S3，可得出结果．
【详解】
解：∵∠ACB=90°，
∴AC2+BC2=AB2，
∴S1+S2=S3，
故答案为：=.
本题考查了勾股定理、正方形面积的计算；熟练掌握勾股定理，由勾股定理得出正方形的面积关系是解决问题的关键．
13、y＝x﹣1．
【解析】
可以先求出点A的坐标，进而知道直线平移的距离，得出点B的坐标，平移前后的k相同，设出平移后的关系式，把点B的坐标代入即可．
【详解】
∵点A（m，1）在反比例函数y＝的图象，
∴1＝，即：m＝2，
∴A（2，1）、B（2，0）
点A在y＝kx上，
∴k＝
∴y＝x
∵将直线y＝x平移2个单位得到直线l，
∴k相等
设直线l的关系式为：y＝x+b，把点B（2，0）代入得：b＝﹣1，
直线l的函数关系式为：y＝x﹣1；
故答案为：y＝x﹣1．
本题考查反比例函数的图象上点的坐标的特点、待定系数法求函数解析式、一次函数和平移等知识，理解平移前后两个因此函数的k值相等，是解决问题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）见解析；（2）.
【解析】
（1）由“ASA”可证△AEF≌△DEC；
（2）由直角三角形的性质可得，即可求BC的长．
【详解】
解：（1）∵四边形ABCD是平行四边形
∴AB∥CD，AD=BC
∴∠EAF=∠D，
∵点E是AD中点，
∴AE=DE，且∠EAF=∠D，∠AEF=∠CED
∴△AEF≌△DEC（ASA）
（2）∵∠FCB=90°，AD∥BC
∴∠CED=90°，且∠D=30°，CD=3cm，
，
，
.
本题考查了平行四边形的性质，全等三角形的判定和性质，熟练运用平行四边形的性质是本题的关键．
15、a（m﹣3）1．
【解析】
先提取公因式，再利用完全平方公式分解因式即可解答
【详解】
原式＝a（m1﹣6m+9）
＝a（m﹣3）1．
此题考查提公因式法和公式法的综合运用，解题关键在于熟练掌握运算法则
16、该市今年居民用水的价格是每立方米2.4元．
【解析】
利用总水费÷单价＝用水量，结合小丽家今年5月的用水量比去年12月的用水量多5m1，进而得出等式即可．
【详解】
设去年居民用水价格为x元/m1，根据题意列方程：，
解得：x＝2，
经检验：x＝2是原方程的根，
∴（1+20%）x＝2.4，
答：该市今年居民用水的价格是每立方米2.4元．
本题考查了分式方程的应用，应用题中一般有三个量，求一个量，明显的有一个量，一定是根据另一量来列等量关系的．分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．
17、 (1)点C的坐标为(4，4)；(2)直线CD的解析式是y=；(3)点F的坐标是(11，4)，(5，-4)或(-3，4)．
【解析】
（1）由OA，OB的长度可得出点A，B的坐标，结合点C为线段AB的中点可得出点C的坐标；
（2）由OD的长度可得出点D的坐标，根据点C，D的坐标，利用待定系数法可求出直线CD的解析式；
（3）设点F的坐标为（m，n），分AC为对角线、AD为对角线及CD为对角线三种情况，利用平行四边形的对角线互相平分可得出关于m，n的二元一次方程组，解之即可得出点F的坐标．
【详解】
(1)∵OA=OB=8，点A在x轴正半轴，点B在y轴正半轴，
∴点A的坐标为(8，0)，点B的坐标为(0，8)．
又∵点C为线段AB的中点，
∴点C的坐标为(4，4)．
(2)∵OD=1，点D在x轴的正半轴，
∴点D的坐标为(1，0)．
设直线CD的解析式为y=kx+b(k≠0)，
将C(4，4)，D(1，0)代入y=kx+b，
得：，
解得：，
∴直线CD的解析式是y=．
(3)存在点F，使以A、C、D、F为点的四边形为平行四边形，设点F的坐标为(m，n)．
分三种情况考虑，如图所示：
①当AC为对角线时，
∵A(8，0)，C(4，4)，D(1，0)，
∴，
解得：，
∴点F1的坐标为(11，4)；
②当AD为对角线时，
∵A(8，0)，C(4，4)，D(1，0)，
∴，
解得：，
∴点F2的坐标为(5，-4)；
③当CD为对角线时，
∵A(8，0)，C(4，4)，D(1，0)，
∴，
解得：，
∴点F3的坐标为(-3，4)．
综上所述，点F的坐标是(11，4)，(5，-4)或(-3，4)．
本题考查了中点坐标公式、待定系数法求一次函数解析式、平行四边形的性质以及解二元一次方程组，解题的关键是：（1）由点A，B的坐标，利用中点坐标公式求出点C的坐标；（2）根据点的坐标，利用待定系数法求出直线CD的解析式；（3）分AC为对角线、AD为对角线及CD为对角线三种情况，利用平行四边形的对角线互相平分找关于m，n的二元一次方程组．
18、 (1)证明见解析；(2)1.
【解析】
（1）只要证明CB=CE，利用等腰三角形的三线合一的性质即可解决问题；
（2）根据CE=CB，求出BC的长即可解决问题.
【详解】
（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CE，
∴∠E=∠ABE，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠E=∠CBE，
∴CB=CE，
∵CF⊥BE，
∴BF=EF．
（2）∵四边形ABCD是平行四边形，
∴AB=CD=8，
∵DE=4，
∴BC=CE=12，
∴平行四边形ABCD的周长为2（AB+BC）=1．
本题考查平行四边形的性质、角平分线的定义、等腰三角形的判定和性质等知识，解题的关键是熟练掌握基本知识.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、10
【解析】
根据勾股定理
c为三角形边长，故c=10.
20、
【解析】
试题分析：根据菱形性质得出AC⊥BD，AO=OC=12，BO=BD=5，根据勾股定理求出AB，根据菱形的面积得出S菱形ABCD=×AC×BD=AB×DE，代入求出即可．
【详解】
∵四边形ABCD是菱形，AC=24，BD=10，
∴AC⊥BD，AO=OC=AC=12，BO=BD=5，
在Rt△AOB中，由勾股定理得：AB=13，
∵S菱形ABCD=×AC×BD=AB×DE，
∴×24×10=13DE，
∴DE=，
故答案为．
本题考查的是菱形的性质及等面积法，掌握菱形的性质，灵活运用等面积法是解题的关键.
21、y＝x+1或y＝x﹣2
【解析】
设反比例解析式为y＝，将B坐标代入直线y＝x﹣2中求出m的值，确定出B坐标，将B坐标代入反比例解析式中求出k的值，即可确定出反比例解析式；当直线向上平移时，过C作CD垂直于y轴，过B作BE垂直于y轴，设y＝x﹣2平移后解析式为y＝x＋b，C坐标为（a，a＋b），△ABC面积＝梯形BEDC面积＋△ABE面积﹣△ACD面积，由已知△ABC面积列出关系式，将C坐标代入反比例解析式中列出关系式，两关系式联立求出b的值，即可确定出平移后直线的解析式；当直线向下平移时，假设平移后与反比例函数图像在第一象限内交于点C'，若平移的距离和向上平移的距离相同，利用△ABC与△ABC'的同底等高，便能得到且它们的面积也相同，皆为18，符合题意，进而得到结果．
【详解】
解：将B坐标代入直线y＝x﹣2中得：m﹣2＝2，解得：m＝4，
则B（4，2），即BE＝4，OE＝2，设反比例解析式为y＝（k≠0），
将B（4，2）代入反比例解析式得：k＝8，则反比例解析式为y＝；
设平移后直线解析式为y＝x＋b，C（a，a＋b），
对于直线y＝x﹣2，令x＝0求出y＝﹣2，得到OA＝2，
过C作CD⊥y轴，过B作BE⊥y轴，
将C坐标代入反比例解析式得：a（a＋b）＝8，
∵S△ABC＝S梯形BCDE＋S△ABE﹣S△ACD＝18，
∴×（a＋4）×（a＋b﹣2）＋×（2＋2）×4﹣×a×（a＋b＋2）＝18，
解得：b＝1，则平移后直线解析式为y＝x＋1．
此时直线y＝x＋1是由y＝x﹣2向上平移9个单位得到的，
同理，当直线向下平移9个单位时，直线解析式为y＝x﹣2﹣9，即：y＝x﹣2
设此时直线与反比例函数图像在第一象限内交于点C'，
则此时△ABC与△ABC'是同底等高的两个三角形，
所以△ABC'也是18，符合题意，
故答案是：y＝x＋1或y＝x﹣2．
此题考查了一次函数与反比例函数的交点问题，涉及的知识有：一次函数与坐标轴的交点，待定系数法求函数解析式，三角形、梯形的面积求法，以及坐标与图形性质，熟练掌握待定系数法是解本题的关键．
22、②③④
【解析】
分析：分别计算该组数据的平均数，众数，方差后找到正确的答案即可．
详解：∵﹣6，﹣3，x，2，﹣1，3的中位数是-1，∴分三种情况讨论：
①若x≤－3，则中位数是（－1－3）÷2=－2，矛盾；
②若x≥2，则中位数是（－1+2）÷2=0.5，矛盾；
③若-3＜x≤－1或－1≤x＜2，则中位数是（－1+x）÷2=－1，解得：x=﹣1；
平均数=（﹣6﹣3﹣1﹣1+2+3）÷6=﹣1．
∵数据﹣1出现两次，出现的次数最多，∴众数为﹣1；
方差=[（﹣6+1）2+（﹣3+1）2+（﹣1+1）2+（2+1）2+（﹣1+1）2+（3+1）2]=9，∴正确的序号是②③；
故答案为②③．
点睛：本题考查了方差、平均数、中位数及众数的知识，属于基础题，掌握各部分的定义及计算方法是解题的关键．
23、y1>y2
【解析】
∵在中，，
∴在函数中，y随x的增大而减小.
又∵，
∴，即空格处应填“>”.
二、解答题（本大题共3个小题，共30分）
24、（1）见解析（2）1.5、1.5（3）216
【解析】
（1）根据学生劳动“1小时”的人数除以占的百分比，求出总人数；
（2）根据统计图中的数据确定出学生劳动时间的众数与中位数即可；
（3）总人数乘以样本中参加义务劳动2小时的百分比即可得．
【详解】
(1)根据题意得：30÷30%=100(人)，
∴学生劳动时间为“1.5小时”的人数为100−(12+30+18)=40(人)，
补全统计图，如图所示：
(2)根据题意得：抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时，
故答案为：1.5、1.5；
(3)1200×18%=216，
答：估算该校学生参加义务劳动2小时的有216人
此题考查扇形统计图，条形统计图，中位数，众数，解题关键在于看懂图中数据
25、（1）4；1；（2）见解析；（3）B；（4）48.
【解析】
（1）根据题目中的数据即可直接确定m和n的值；
（2）根据（1）的结果即可直接补全直方图；
（3）根据中位数的定义直接求解；
（4）利用总人数乘以对应的比例即可求解．
【详解】
解：（1）由记录的数据可知，7500≤x＜8500的有8430、8215、7638、7850这4个，即m=4；
9500≤x＜10500的有9865这1个，即n=1．
故答案为4；1；
（2）如图：
（3）由于一共20个数据，其中位数是第10、11个数据的平均数，
而第10、11个数据的平均数均落在B组，
∴这20名“健步走运动”团队成员一天行走步数的中位数落在B组；
故答案为B；
（4）120×=48（人），
答：估计其中一天行走步数不少于7500步的有48人．
故答案为48.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
26、船向岸边移动了大约3.3m．
【解析】
由题意可求出CD长，在中分别用勾股定理求出AD,AB长，作差即可.
【详解】
解：∵在中，，，，
∴．
∵此人以0.5m/s的速度收绳，6s后船移动到点D的位置，
∴．
∴．
∴．
答：船向岸边移动了大约3.3m．
本题是勾股定理的应用，灵活运用勾股定理求线段长是解题的关键,
题号
一
二
三
四
五
总分
得分
批阅人
甲
乙
丙
丁
平均数
80
85
85
80
方 差
42
42
54
59
组别
步数分组
频数
A
5500≤x＜6500
2
B
6500≤x＜7500
10
C
7500≤x＜8500
m
D
8500≤x＜9500
3
E
9500≤x＜10500
n