2021-2022学年广东省广州市南沙区六年级（上）期末数学试卷

这是一份2021-2022学年广东省广州市南沙区六年级（上）期末数学试卷，共22页。试卷主要包含了数学四基，数学眼光，数学思维，数学语言，应用创新等内容，欢迎下载使用。


1．（1 分）自行车的车轮滚动一周，这一周的长度就是这个车轮的（）
A．半径B．直径C．周长D．面积
2．（1 分）一根绳长 a 米，如果用去它的，用去了（）米。
A．a﹣ B． C．aD．（1﹣） a
3．（1 分）某小学组织 100 名学生参加植树活动，当天有 2 人请假，该活动的出勤率是（）
A．2%B．98%C．100%D．102%
4．（1 分）因为×＝1，所以（）
A． 是倒数B． 是倒数
C． 和 互为倒数D．1 是倒数
5．（1 分）小明在图书馆借了一本中华英雄人物的故事书，全书 60 页，第一天读了全书的，第二天读的页数是第一天的 ，第二天读了（）页。
A．7B．8C．9D．10 6．（1 分）一个圆的半径是 2 分米，那么这个圆的周长和面积比较，（）
A．周长大B．面积大C．大小相等D．无法比较
7．（1 分）在“双减”政策下，学校更关注同学们的睡眠时间，为直观看出同学们睡眠时间与全天时间的关系，可以绘制成（）统计图。
A．条形B．折线C．扇形D．表格
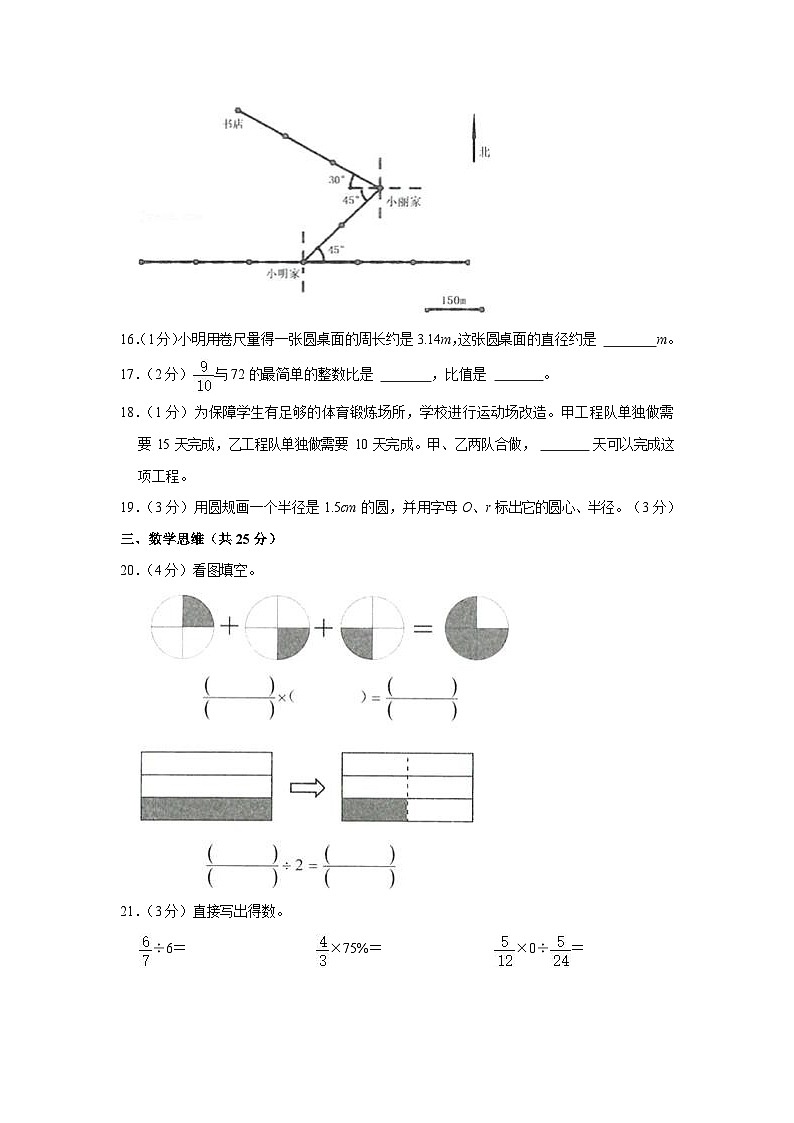
8．（1 分）在计算÷3 时，下面的三种算法中不正确的是（）
A． ÷3＝ ×3B． ÷3＝ × C． ÷3＝
9．（1 分）下面图形中哪一个角是圆心角？（）
A．B．
C．
10．（1 分）一个圆环（如图），内圆半径是 2dm，外圆半径是 4dm。计算这个圆环的面积正确的算式是（）
A．3.14×（4﹣2）2B．3.14×（42﹣22） C．3.14×（4+2）2
二、数学眼光（每空 1 分，共 27 分）
11．（2 分）的倒数是 ，0.1 的倒数是 。
12．（4 分）5：8＝＝ ÷40＝ （填小数）＝ %
13．（3 分）在横线里填上“＞”“＜”或“＝”。
18× 18×0.10.6×10%11÷ 11×
14．（4 分）40 公顷的是 公顷，20m 比 50m 米少 %。 是的 2 倍，比 30 吨多是吨。
15．（7 分）根据下面的描述，在平面图上标出各场所的位置。
小明家在小丽家西偏南°方向m 米处。
小红家在小明家正东方向 450m 处，请你在图中标出小红家的位置。
） 请说一说小明从家出发去书店所走的路线。小明从家出发， 向偏45°方向，走 300m 到小丽家，再往偏°方向走米到书店。
16．（1 分）小明用卷尺量得一张圆桌面的周长约是 3.14m，这张圆桌面的直径约是 m。
17．（2 分）与 72 的最简单的整数比是 ，比值是 。
18．（1 分）为保障学生有足够的体育锻炼场所，学校进行运动场改造。甲工程队单独做需要 15 天完成，乙工程队单独做需要 10 天完成。甲、乙两队合做， 天可以完成这项工程。
19．（3 分）用圆规画一个半径是 1.5cm 的圆，并用字母 O、r 标出它的圆心、半径。（3 分）三、数学思维（共 25 分）
20．（4 分）看图填空。
21．（3 分）直接写出得数。
÷6＝×75%＝×0÷＝
22．（12 分）用你喜欢的方法计算。
（1）×÷ （2）×+× （3）×16﹣ （4）（15﹣14×）÷
23．（6 分）解方程。
（1） x＝18（2） x÷2＝0.5
四、数学语言（共 34 分）
24．（8 分）把补充的条件与算式连起来。
养殖场养鸡 120 只，，养鸭多少只？
（1）鸡的只数比鸭多 A.120×（1+ ）
（2）鸭的只数比鸡多 B.120×（1﹣ ）
（3）鸡的只数比鸭少 C.120÷（1+ ）
（4）鸭的只数比鸡少 D.120÷（1﹣ ）
25．（6 分）学校合唱队有 54 名队员，男生与女生的人数比是 4：5。
如果把合唱队学生看作一个整体，男生占合唱队的，女生占合唱队的。
学校合唱队的男、女生各有多少名？
26．（10 分）文化广场需要建造的一个圆形花坛，花坛半径是 3m。
这圆形花坛的周长是多少 m？
这圆形花坛面积是多少 m2？
如果在圆形花坛的周围修一条宽 2 米的环形小路（如图）。小路的面积是多少 m2？
27．（10 分）某小学劳动实践基地有一块 500m2 的菜地，种植了 4 种蔬菜。其中萝卜的面积和玉米一样多，白菜面积是玉米的一半。
如图属于统计图，根据已知信息把它补充完整。
玉米的种植面积是多少平方米？
萝卜的种植面积比白菜多多少平方米？
五、应用创新（共 4 分）
28．（4 分）一次科技展活动邀请近千名学生参加，实际参加的学生人数达三位数，但具体
人数不详，其中女生人数是男生人数的 ，试分析参加活动的男生和女生分别可能有多 少人？把分析过程写出来。
2021-2022 学年广东省广州市南沙区六年级（上）期末数学试卷
参考答案与试题解析
一、数学四基（单选题，请把相应的序号填在括号里，每小题 1 分，共 10 分）
1．（1 分）自行车的车轮滚动一周，这一周的长度就是这个车轮的（）
A．半径B．直径C．周长D．面积
【分析】根据圆的周长的意义可知，自行车的车轮滚动一周，这一周的长度就是这个车 轮的周长。据此解答。
【解答】解：自行车的车轮滚动一周，这一周的长度就是这个车轮的周长。 故选：C。
【点评】此题考查的目的是理解掌握圆周长的意义及应用。
2．（1 分）一根绳长 a 米，如果用去它的，用去了（）米。
A．a﹣ B． C．aD．（1﹣） a
【分析】根据分数乘法的意义，求一个数的几分之几是多少用除法计算，据此列式解决 问题。
【解答】解：一根绳长 a 米，如果用去它的，用去了 a 米。
故选：C。
【点评】解答此题的关键是正确理解分数乘法的意义。
3．（1 分）某小学组织 100 名学生参加植树活动，当天有 2 人请假，该活动的出勤率是（）
A．2%B．98%C．100%D．102%
【分析】出勤率＝出勤人数÷总人数×100%，由此代入数据求解。
【解答】解：（100﹣2）÷100×100%
＝0.98×100%
＝98%
答：该活动的出勤率是 98%。故选：B。
【点评】此题属于百分率问题，都是用一部分数量（或全部数量）除以全部数量乘 100%。4．（1 分）因为 × ＝1，所以（）
A． 是倒数B． 是倒数
C． 和 互为倒数D．1 是倒数
【分析】若两个数的乘积是 1，我们就称这两个数互为倒数，据此解答。
【解答】解：因为因为 × ＝1，所以 和 互为倒数。故选：C。
【点评】此题主要考查了倒数的定义：若两个数的乘积是 1，我们就称这两个数互为倒数。
5．（1 分）小明在图书馆借了一本中华英雄人物的故事书，全书 60 页，第一天读了全书的，第二天读的页数是第一天的 ，第二天读了（）页。
A．7B．8C．9D．10
【分析】用全书的总页数乘 ，计算出第一天读的页数，再用第一天读的页数乘 ，计算出第二天读的页数。
【解答】解：60×
＝10×
＝9（页）
答：第二天读了 9 页。故选：C。
【点评】本题考查分数乘法应用题，解题关键是先找出题目中的单位“1”是哪个量，再 根据一个数乘分数的意义，列式计算。
6．（1 分）一个圆的半径是 2 分米，那么这个圆的周长和面积比较，（）
A．周长大B．面积大C．大小相等D．无法比较
【分析】根据圆的周长公式：C＝2πr，圆的面积公式：S＝πr2，因为周长和面积不是同 类量，所以无法比较。据此解答。
【解答】解：因为周长和面积不是同类量，所以无法比较。 故选：D。
【点评】此题考查的目的是理解掌握圆的周长、面积的意义及应用，关键是明确：只有 同类量，才能比较大小。
7．（1 分）在“双减”政策下，学校更关注同学们的睡眠时间，为直观看出同学们睡眠时间
与全天时间的关系，可以绘制成（ ）统计图。
A．条形B．折线C．扇形D．表格
【分析】条形统计图能很容易看出数量的多少；折线统计图不仅容易看出数量的多少， 而且能反映数量的增减变化情况；扇形统计图能反映部分与整体的关系；由此根据情况 选择即可。
【解答】解：在“双减”政策下，学校更关注同学们的睡眠时间，为直观看出同学们睡 眠时间与全天时间的关系，可以绘制成扇形统计图。
故选：C。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
8．（1 分）在计算÷3 时，下面的三种算法中不正确的是（）
A． ÷3＝ ×3B． ÷3＝ × C． ÷3＝
【分析】分数除以整数（0 除外），可以用分数乘这个数的倒数，也可以用分数的分子除以这个整数，分母不变。
【解答】解：A. ÷3＝ ，直接用分数乘的整数，所以计算错误；
B.÷3＝ × ，符合分数除以整数的计算方法，计算正确；
C.÷3＝ ，符合分数除以整数的计算方法，计算正确。 故选：A。
【点评】熟练掌握分数除以整数的计算方法是解题的关键。
9．（1 分）下面图形中哪一个角是圆心角？（）
A． B．
C．
【分析】一条弧和经过这条弧两端的两条半径所围成的图形叫扇形，据此判断即可。
【解答】解：是圆心角。故选：A。
【点评】此题考查了平面图形的定义，要熟练掌握。
10．（1 分）一个圆环（如图），内圆半径是 2dm，外圆半径是 4dm。计算这个圆环的面积正确的算式是（）
A．3.14×（4﹣2）2B．3.14×（42﹣22） C．3.14×（4+2）2
【分析】根据环形面积公式：S＝π（R2﹣r2），把数据代入公式解答。
【解答】解：3.14×（42﹣22）
＝3.14×（16﹣4）
＝3.14×12
＝37.68（平方分米）
答：这个圆环的面积是 37.68 平方分米。故选：B。
【点评】此题主要考查环形面积公式的灵活运用，关键是熟记公式。 二、数学眼光（每空 1 分，共 27 分）
11．（2 分）的倒数是 ，0.1 的倒数是 10。
【分析】若两个数的乘积是 1，我们就称这两个数互为倒数，据此解答。
【解答】解： 的倒数是 ，0.1 的倒数是 10。故答案为： ，10。
【点评】本题考查了倒数的含义。
12．（4 分）5：8＝＝ 25÷40＝ 0.625（填小数）＝ 62.5%
【分析】根据比与分数的关系 5：8＝，再根据分数的基本性质分子、分母都乘 3 就是；
根据比与除法的关系 5：8＝5÷8，再根据商不变的性质被除数、除数都乘 5 就是 25÷40； 5÷8＝0.625；把 0.625 的小数点向右移动两位，添上百分号就是 62.5%。
【解答】解：5：8＝ ＝25÷40＝0.625＝62.5%
故答案为：24，25，0.625，62.5。
【点评】此题主要是考查除法、小数、分数、百分数、比之间的关系及转化。利用它们 之间的关系和性质进行转化即可。
13．（3 分）在横线里填上“＞”“＜”或“＝”。
18× ＜ 18×0.1 ＝＞ 0.6×10% 11÷ ＞ 11×
【分析】根据分数乘法与分数除法的计算方法，分别计算出每组算式的结果，再比较大 小即可。
【解答】解： ，15＜18；
，0.6×10%＝0.06，0.6＝0.6；
， ， 。
18× ＜18×0.1＝0.6×10%11÷ ＞11×
故答案为：＜；＝；＞。
【点评】本题解题关键是熟练掌握分数乘法与分数除法的计算方法和分数大小比较的方 法。
14．（4 分）40 公顷的是 30公顷，20m 比 50m 米少 60%。
是的 2 倍，比 30 吨多是 45吨。
【分析】求 40 公顷的是多少公顷，就是求 40 公顷乘的积；求 20 米比 50 米少百分
之几，就是求（50﹣20）米是 50 米的百分之几；求是哪个数的 2 倍，就是求除以 2
的商；求比 30 吨多 是多少吨，就是求 30 吨的（1+ ）是多少吨。
【解答】解：40× ＝30（公顷）
（50﹣20）÷50
＝30÷50
＝0.6
＝60%
÷2＝
30×（1+ ）
＝30×
＝45（吨）
故答案为：30，60， ，45。
【点评】本题考查了利用分数的乘除及分数四则混合运算解决问题，需准确分析题意。
15．（7 分）根据下面的描述，在平面图上标出各场所的位置。
小明家在小丽家西偏南 45°方向 300m 米处。
小红家在小明家正东方向 450m 处，请你在图中标出小红家的位置。
请说一说小明从家出发去书店所走的路线。小明从家出发，向 东 偏 北 45°方向，走 300m 到小丽家，再往 西 偏 北30°方向走 450米到书店。
【分析】首先确定图上方向是“上北下南，左西右东”，然后根据各个地点之间的位置关系结合题意解答即可。
【解答】解：（1）150×2＝300（米）
答：小明家在小丽家西偏南 45°方向 300m 米处。
（2）作图如下：
（3）150×3＝450（米）
答：小明从家出发去书店所走的路线。小明从家出发，向东偏北 45°方向，走 300m 到小丽家，再往西偏 30°方向走 450 米到书店。
故答案为：45，300；东，北，西，北，30，450。
【点评】本题考查了位置与方向及路线图知识，结合题意分析解答即可。
16．（1 分）小明用卷尺量得一张圆桌面的周长约是 3.14m，这张圆桌面的直径约是 1m。
【分析】根据圆的周长公式：C＝πd，那么 d＝C÷π，把数据代入公式解答。
【解答】解：3.14÷3.14＝1（米） 答：这张圆桌面的直径是 1 米。故答案为：1。
【点评】此题主要考查圆的周长公式的灵活运用，关键是熟记公式。
17．（2 分）与 72 的最简单的整数比是 1：80，比值是 。
【分析】（1）根据比的基本性质，即比的前项和后项同时乘或除以一个相同的数（0 除外） 比值不变，进而把比化成最简比；
（2）用比的前项除以后项，所得的商即为比值。
【解答】解：（1）：72＝1：80
（2） ：72＝
故答案为：1：80， 。
【点评】此题主要考查了化简比和求比值的方法，另外还要注意化简比的结果是一个比， 它的前项和后项都是整数，并且是互质数；而求比值的结果是一个商，可以是整数、小数或分数。
18．（1 分）为保障学生有足够的体育锻炼场所，学校进行运动场改造。甲工程队单独做需要 15 天完成，乙工程队单独做需要 10 天完成。甲、乙两队合做， 6 天可以完成这项工程。
【分析】把这项工程的工作总量看作单位“1”，则甲队的工作效率是，乙队的工作效
率是 ，利用工作时间＝工作总量÷甲乙的工作效率和，求出完成的时间。
【解答】解：
＝
＝6（天）
答：6 天可以完成这项工程。故答案为：6。
【点评】本题考查工程问题的解题方法，解题关键是要把工作总量看作单位“1”，利用工作时间＝工作总量÷甲乙的工作效率和，求出完成的时间。
19．（3 分）用圆规画一个半径是 1.5cm 的圆，并用字母 O、r 标出它的圆心、半径。（3 分）
【分析】先确定圆心，用圆规有针的一脚固定在圆心，然后以圆规两脚之间的距离为 1.5 厘米进行旋转一周，得到的图形就是我们要画的圆；圆心用字母“O”表示；半径用字母“r”表示，由此求解。
【解答】解：画图如下：
【点评】本题主要考查了圆的画法，注意圆规的两脚分开的距离是圆的半径。 三、数学思维（共 25 分）
20．（4 分）看图填空。
【分析】把一个圆的面积看作单位“1”，把这平均分成 4 份，每份是它的 ，3 个 是乘 3，积相当于一个圆中 3 份涂色，是这个圆的 。
把一个长方形的面积看作单位“1”，把它平均分成 3 份，每份是它的 ，再把 平均分
成 2 份，求每份是多少，用除以 2，商相当于把这个长方形平均分成 6 份，表示其中 1
份，是这个长方形的 。
【解答】解：
【点评】此题考查的分数的意义、分数乘法的意义、分数除法的意义。
21．（3 分）直接写出得数。
÷6＝×75%＝×0÷ ＝
【分析】根据分数、百分数乘除法的计算方法直接进行口算即可。
【解答】解：
÷6＝ ×75%＝1×0÷ ＝0
【点评】本题考查了基本的运算，注意运算数据和运算符号，细心计算即可。
22．（12 分）用你喜欢的方法计算。
（1）×÷ （2）×+× （3）×16﹣ （4）（15﹣14×）
÷
【分析】（1）将除法化成乘法计算。
利用乘法分配律计算。
利用乘法分配律计算。
先算括号里的乘法，再算括号里的减法，最后算括号外的除法。
【解答】解：（1）×÷
＝ × ×
＝
（2） × + ×
＝ ×（ + ）
＝ ×1
＝
（3） ×16﹣
＝ ×（16﹣1）
＝×15
＝8
（4）（15﹣14×）÷
＝（15﹣8）×
＝7×
＝
【点评】本题考查了分数的四则混合运算，需熟练使用法则，灵活使用运算律。
23．（6 分）解方程。
（1） x＝18（2） x÷2＝0.5
【分析】（1）方程的两边同时除以 即可。
（2）方程的两边先同时乘 2，然后方程的两边同时除以。
【解答】解：（1）x＝18
x÷ ＝18÷
x＝30
（2） x÷2＝0.5
x÷2×2＝0.5×2
x÷ ＝1÷
x＝4
【点评】本题考查了分数方程的解法，解题过程需利用等式的性质。 四、数学语言（共 34 分）
24．（8 分）把补充的条件与算式连起来。
养殖场养鸡 120 只， （1）、（2）、（3）、（4） ，养鸭多少只？
（1）鸡的只数比鸭多A.120×（1+ ）
（2）鸭的只数比鸡多 B.120×（1﹣ ）
（3）鸡的只数比鸭少 C.120÷（1+ ）
（4）鸭的只数比鸡少 D.120÷（1﹣ ）
【分析】（1）养殖场养鸡 120 只，鸡的只数比鸭多，求养鸭多少只，是将鸭的只数看作单位“1”，列式为 120÷（1+）。
养殖场养鸡 120 只，鸭的只数比鸡多，求养鸭多少只，是将鸡的只数看作单位“1”，列式为 120×（1﹣）。
养殖场养鸡 120 只，鸡的只数比鸭少，求养鸭多少只，是将鸭的只数看作单位“1”，列式为 120÷（1﹣）。
养殖场养鸡 120 只，鸭的只数比鸡少，求养鸭多少只，是将鸡的只数看作单位“1”，列式为 120×（1﹣）
【解答】解：
【点评】本题考查了利用分数乘除法解决问题，需准确分析问题与条件之间的关系，确 定出补充的条件后准确选择对应的算式。
25．（6 分）学校合唱队有 54 名队员，男生与女生的人数比是 4：5。
如果把合唱队学生看作一个整体，男生占合唱队的，女生占合唱队的
。
学校合唱队的男、女生各有多少名？
【分析】（1）把男生人数看作“4”，则女生人数是“5”，合唱一共有（“（4+5）”人，分别用男生人数、女生人数除以合唱队人数。
（2）把合唱队人数平均分成（4+5）份，先用除法求出 1 份的人数，再作乘法分别求出
4 份（男生）、5 份（女生）人数。
【解答】解：（1）4+5＝9 4÷9＝
5÷9＝
答：男生占合唱队的 ，女生占合唱队的 。
（2）54÷（4+5）
＝54÷9
＝6（人）
6×4＝24（人）
6×5＝30（人）
答：学校合唱队的男生 24 人，女生 30 人。
故答案为： ， 。
【点评】（1）根据男、女生人数比，分别求出男生人数、女生人数、总人数，再根据求 一个数的几分之几是多少，用这个数除以另一个数解答；（2）亦可根据男、女生人数的比，求出男、女生各占总人数的几分之几，再根据分数乘法的意义解答。
26．（10 分）文化广场需要建造的一个圆形花坛，花坛半径是 3m。
这圆形花坛的周长是多少 m？
这圆形花坛面积是多少 m2？
如果在圆形花坛的周围修一条宽 2 米的环形小路（如图）。小路的面积是多少 m2？
【分析】（1）已知花坛半径是 3m，根据圆的周长公式解答即可；
已知花坛半径是 3m，根据圆的面积公式解答即可；
根据题意可知，小路的面积是环形面积，根据环形面积公式：S＝π（R2﹣r2），把
数据代入公式解答。
【解答】解：（1）2×3.14×3＝18.84（平方米）答：这圆形花坛的周长是 18.84 米。
（2）3.14×32
＝3.14×9
＝28.26（平方米）
答：这圆形花坛的面积是 28.26 平方米。
（3）3.14×（52﹣32）
＝3.14×（25﹣9）
＝3.14×16
＝50.24（平方米）
答：小路的面积 50.24 平方米。
【点评】此题主要考查圆的周长、面积和环形面积公式的灵活运用，关键是熟记公式。
27．（10 分）某小学劳动实践基地有一块 500m2 的菜地，种植了 4 种蔬菜。其中萝卜的面积和玉米一样多，白菜面积是玉米的一半。
如图属于 扇形 统计图，根据已知信息把它补充完整。
玉米的种植面积是多少平方米？
萝卜的种植面积比白菜多多少平方米？
【分析】（1）右图为扇形统计图，玉米占了 30%，萝卜的面积和玉米一样多，可知萝卜也是 30%，白菜面积是玉米的一半，用玉米所占的百分比除以 2，即可求出白菜所占的百分比，最后用 1 减去玉米、萝卜、白菜所占的百分比，可得出茄子所占的百分比；
用总面积乘玉米所占的百分比，即可求出玉米的种植面积是多少平方米；
分别算出萝卜和白菜的种植面积，然后再相减即可。
【解答】解：（1）如图属于扇形统计图，萝卜：20%
白菜：30%÷2＝15%
茄子：1﹣20%﹣30%﹣15%＝25%
（2）500×30%＝150（平方米）
答：玉米的种植面积是 150 平方米。
（3）萝卜的种植面积：500×30%＝150（平方米） 白菜的种植面积：500×15%＝75（平方米）
多：150﹣75＝75（平方米）
答：萝卜的种植面积比白菜多 75 平方米。故答案为：扇形。
【点评】此题考查学生对统计图表的理解和应用。进一步考查学生的理解能力。 五、应用创新（共 4 分）
28．（4 分）一次科技展活动邀请近千名学生参加，实际参加的学生人数达三位数，但具体
人数不详，其中女生人数是男生人数的 ，试分析参加活动的男生和女生分别可能有多 少人？把分析过程写出来。
【分析】根据“女生人数是男生人数的 ”，可以推算出女生人数与男生人数的比是 5：6，
则参加科技展的总人数是 11 份，那么参加科技展的总人数是 11 的倍数，进而推算出参加活动的男生和女生分别可能有多少人。
【解答】答：接近 1000，并且是 11 的倍数的数可能是 990。
5+6＝11
990× ＝450（人）
990× ＝540（人）
答：参加活动的男生有 450 人，女生有 540 人。（答案不唯一）
【点评】本题解题关键是理解参加科技展的总人数是 11 的倍数，再根据分数乘法的意义， 列式计算。