

广东省广州市海珠区2021-2022学年六年级上学期期末数学试卷
展开1.在横线里填上“>”“<”或“=”。
2.= :10=12÷ = (小数)= %
3.把:化成最简单的整数比是 ,比值是 。
4.由“已修这条路全长的60%”可求得:已修的长度是全长的,已修长度与未修长度的比是 。
5.运一堆货物,甲车队单独运要6次才能运完,乙车队单独运要12次才能运完。如果两车队合运, 次可运完。
6.图中三角形ABC是一个等边三角形,边长是10m,那么点A在点B 偏 方向 m处。
7.某校六年级学生300人参加某次体育测试,达标率是70%,这次测试一共有 人达标。
8.红花有20朵,黄花比红花少4朵,黄花比红花少 %。
9.一个圆桌面的直径是2m,这个圆桌面的周长是 m,面积是 m2。
10.湖边种了40棵柳树,是桃树棵数的,榕树的棵数是桃树棵数的65%。湖边种了 棵榕树。
11.如图圆环的面积是 cm2。
二、选择。(选择正确答案的序号填在括号里。)
12.下面的说法,正确的是( )
A.圆周率π是圆的周长与它半径的比值
B.比较两个扇形的面积,圆心角大的那个扇形,面积也一定较大
C.圆内最长的线段是圆的直径
13.根据“海狮的寿命是海象的”写数量关系式,正确的是( )
A.海狮的寿命×=海象的寿命
B.海象的寿命×=海狮的寿命
C.海象的寿命÷=海狮的寿命
14.大圆的半径与小圆半径的比是2:1,则大圆的周长与小圆周长的比是 ,大圆的面积与小圆面积的比是 。
A.2:1
B.4:1
C.8:1
15.某种商品10月的价格比9月上涨了20%,11月的价格比10月又下降了20%。11月的价格跟9月的比,( )
A.上涨了B.没变C.下降了
16.下面三个图形中阴影部分都是扇形,它们的半径都相等,比较它们阴影部分的面积,( )
A.三个都相等
B.只有图2和图3的面积相等
C.三个都不相等
三、计算。
17.直接写出计算结果。
18.用递等式计算下面各题,怎样简便就怎样算。
19.解方程。
x+3=9
四、操作。
20.在右面的空白处画一个半径是2cm的圆,并在圆中画一个圆心角是120°的扇形。
21.根据下面的描述,在平面图上标出各场所的位置及路线图。
(1)体育馆在学校东偏北30°方向800m处。
(2)小青从学校出发,向正西方向走了400m后,再往西偏南40°的方向走了1.2km,到达少年宫。
五、统计。
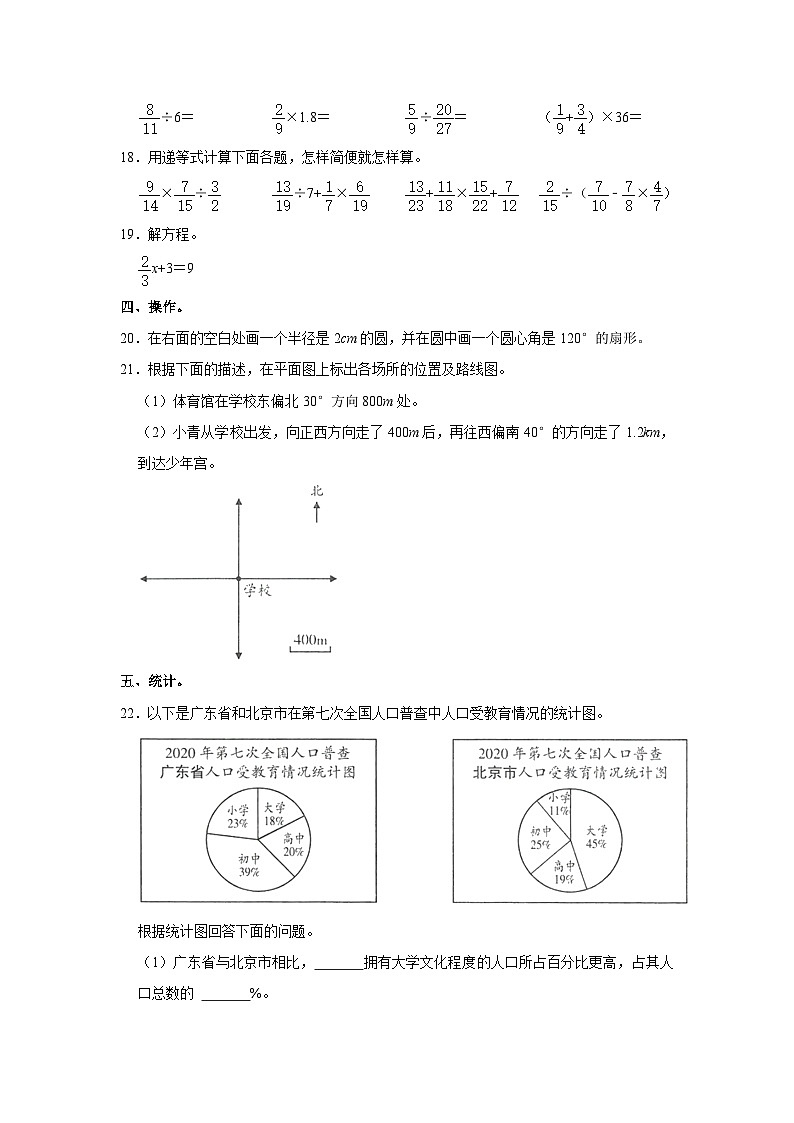
22.以下是广东省和北京市在第七次全国人口普查中人口受教育情况的统计图。
根据统计图回答下面的问题。
(1)广东省与北京市相比, 拥有大学文化程度的人口所占百分比更高,占其人口总数的 %。
(2)在广东省,平均每100人中有 人拥有大学文化程度。
(3)下面的说法正确吗?正确的在括号里打“√”,错误的打“×”。
①两个统计图都是把全国人口总数看作单位“1”。 (判断对错)
②北京市拥有大学文化程度的人口数一定比广东省拥有的人口数多。 (判断对错)
23.下面的数据,分别用哪种统计图表示最合适?请把正确答案的序号填在括号里。
①扇形
②条形
③折线
(1)某班学生各身高段人数占全班人数的百分比情况。
用 统计图
(2)小琪2019﹣2021年的身高变化情况。
用 统计图
(3)某学习小组三名同学的身高情况。
用 统计图
六、只列式,不计算。
24.只列式,不计算。
25.一块长方形地,宽是40m,长是宽的,这块长方形地的面积是多少平方米?
26.牛郎星的运行速度是每秒26千米,织女星的运行速度是每秒14千米,织女星的运行速度比牛郎星慢百分之几?
七、解决问题。
27.学校篮球小组有学生50人,昨天有2人请假。篮球小组昨天的出勤率是多少?
28.张叔叔开车从广州到深圳办事,已经行驶了全程的,还需行驶100千米才到办事地点。张叔叔从广州到深圳一共要行驶多少千米?
29.目前世界上最高的鸟是鸵鸟,最高的哺乳动物是长颈鹿。如图,这只长颈鹿的身高是多少厘米?
30.张大爷家有一块面积为150m2的菜地,准备种上萝卜和青菜。萝卜地和青菜地的面积比是3:2,这两块地的面积分别是多少平方米?
31.一个运动场(如图),两端是半圆形,中间是长方形。
(1)沿着这个运动场跑1圈,要跑多少米?
(2)给这个运动场铺上草坪,一共要铺多少平方米?
2021-2022学年广东省广州市海珠区六年级(上)期末数学试卷(解析版)
一、填空。
1.在横线里填上“>”“<”或“=”。
【分析】(1)大于1,所以×大于,÷小于,据此比较。
(2) 小于1,所以10×小于10,10+大于10,据此比较。
【解答】解:
故答案为:>,<。
2.= 8 :10=12÷ 15 = 0.8 (小数)= 80 %
【分析】根据分数与除法的关系,比的基本性质,分数化成小数的方法,以及小数化成百分数的方法解答。
【解答】解:=4:5=8:10
4:5=(4×3):(5×3)=12÷15=0.8=80%
故答案为:8,15,0.8,80。
3.把:化成最简单的整数比是 4:3 ,比值是 。
【分析】(1)根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外),比值不变,进而把比化成最简比。
(2)用比的前项除以后项,所得的商即为比值。
【解答】解:(1):
=(×):(×)
=4:3
(2):
=÷
=
故答案为:4:3;。
4.由“已修这条路全长的60%”可求得:已修的长度是全长的,已修长度与未修长度的比是 3:2 。
【分析】把全长看作单位“1”,根据百分数化成分数的方法,把60%化成,那么未修的占全长的(1﹣60%),再根据比的意义解答即可。
【解答】解:60%=
60%:(1﹣60%)
=60%:40%
=3:2
答:已修的长度是全长的,已修长度与未修长度的比是3:2。
故答案为:,3:2。
5.运一堆货物,甲车队单独运要6次才能运完,乙车队单独运要12次才能运完。如果两车队合运, 4 次可运完。
【分析】把这批货物的总量看成单位“1”,甲每次运,乙每次运,二者的和是合运一次占总量的几分之几,用总量除以每次运的量就是运的次数。
【解答】解:1÷(+)
=1÷
=4(次)
答:4次可以运完。
故答案为:4。
6.图中三角形ABC是一个等边三角形,边长是10m,那么点A在点B 东 偏 北60° 方向 10 m处。
【分析】根据等边三角形的性质及三角形内角和定理,等边三角形的每个内角都是60°;根据平面图形的方向的辨别“上北下南,左西右东”,以点B的位置为观测点,即可确定点A的方向,点A到点B的距离已知。
【解答】解:如图:
三角形ABC是一个等边三角形,边长是10m,那么点A在点B东偏北60°方向10m处。
故答案为:东,北60°,10。
7.某校六年级学生300人参加某次体育测试,达标率是70%,这次测试一共有 210 人达标。
【分析】把某校六年级的总人数看作单位“1”,达标率是70%,求达标的学生人数,根据求一个数的百分之几是多少,用乘法解答即可。
【解答】解:300×70%=210(人)
答:这次测试一共有210人达标。
故答案为:210。
8.红花有20朵,黄花比红花少4朵,黄花比红花少 20 %。
【分析】用黄花和红花的数量差除以红花的数量,就是黄花比红花少百分之几。
【解答】解:4÷20=20%;
答:黄花比红花少 20%。
故答案为:20。
9.一个圆桌面的直径是2m,这个圆桌面的周长是 6.28 m,面积是 3.14 m2。
【分析】根据圆的周长公式:C=πd;圆的面积公式S=πr2计算即可求解。
【解答】解:3.14×2=6.28(米)
3.14×(2÷2)2
=3.14×1
=3.14(平方米)
答:它的周长是6.28米,面积是3.14平方米。
故答案为:6.28,3.14。
10.湖边种了40棵柳树,是桃树棵数的,榕树的棵数是桃树棵数的65%。湖边种了 60 棵榕树。
【分析】根据题意,先把桃树的棵数看成单位“1”,柳树的棵数是桃树的,用柳树的棵数除以即可求出桃树的棵数;榕树的棵数是桃树棵数的65%,是把桃树的棵数看成单位“1”,据此解答即可。
【解答】解:40÷×60%
=100×60%
=60(棵)
答:湖边种了60棵榕树。
故答案为:60。
11.如图圆环的面积是 21.98 cm2。
【分析】利用圆环的面积公式:S=π(R2﹣r2),把数代入计算即可。
【解答】解:3.14×(42﹣32)
=3.14×(16﹣9)
=3.14×7
=21.98(平方厘米)
答:圆环的面积是21.98平方厘米。
故答案为:21.98。
二、选择。(选择正确答案的序号填在括号里。)
12.下面的说法,正确的是( )
A.圆周率π是圆的周长与它半径的比值
B.比较两个扇形的面积,圆心角大的那个扇形,面积也一定较大
C.圆内最长的线段是圆的直径
【分析】根据圆的认识可知,圆周率π是圆的周长与它直径的比值;比较两个半径相同的扇形的面积,圆心角大的那个扇形,面积也一定较大;圆内最长的线段是圆的直径,据此解答即可。
【解答】解:A.圆周率π是圆的周长与它直径的比值,所以原说法错误;B.比较两个半径相同的扇形的面积,圆心角大的那个扇形,面积也一定较大,所以原说法错误;C.圆内最长的线段是圆的直径,正确。
故选:C。
13.根据“海狮的寿命是海象的”写数量关系式,正确的是( )
A.海狮的寿命×=海象的寿命
B.海象的寿命×=海狮的寿命
C.海象的寿命÷=海狮的寿命
【分析】将海象的寿命看作单位“1”,它的就等于海狮的寿命。据此解答。
【解答】解:由“海狮的寿命是海象的”可知,海象的寿命×=海狮的寿命。
故选:B。
14.大圆的半径与小圆半径的比是2:1,则大圆的周长与小圆周长的比是 A ,大圆的面积与小圆面积的比是 B 。
A.2:1
B.4:1
C.8:1
【分析】根据题干,设小圆的半径是1,则大圆的半径就是2,据此分别计算出它们的直径、周长、面积即可解答问题。
【解答】解:小圆的半径是1,则大圆的半径就是2,
则大圆直径是小圆直径的比:(2×2):(1×2)=2:1
大圆周长是小圆周长的(2π×2)÷(2π×1)=2倍
大圆面积是小圆面积的:(π×22)÷(π×12)=4倍
答:大圆的半径与小圆半径的比是2:1,则大圆的周长与小圆周长的比是2:1,大圆的面积与小圆面积的比是4:1。
故答案为:A,B。
15.某种商品10月的价格比9月上涨了20%,11月的价格比10月又下降了20%。11月的价格跟9月的比,( )
A.上涨了B.没变C.下降了
【分析】把9月份的价格看作单位“1”,则10月份的价格是9月份的1+20%;再把10月份的价格看作单位“1”,则11月份的价格是10月份的1﹣20%;根据分数乘法的意义,则11月份的价格是9月份的(1+20%)×(1﹣20%);然后再比较上涨了还是下降了。
【解答】解:1×(1+20%)×(1﹣20%)
=1×1.2×0.8
=0.96
=96%
因为96%<1,所以价格下降了。
故选:C。
16.下面三个图形中阴影部分都是扇形,它们的半径都相等,比较它们阴影部分的面积,( )
A.三个都相等
B.只有图2和图3的面积相等
C.三个都不相等
【分析】逐个选项分析面积与小圆面积之间的关系,得出结论。
【解答】解:图1的阴影部分的面积等于小圆的面积;图2的阴影部分的面积也等于小圆的面积,图3的阴影部分也的面积等于小圆的面积。所以三个都相等。
故选:A。
三、计算。
17.直接写出计算结果。
【分析】根据分数、小数、百分数加减乘除法的计算方法进行解答即可。
【解答】解:
18.用递等式计算下面各题,怎样简便就怎样算。
【分析】(1)从左向右进行计算;
(2)先把除法化成乘法,再运用乘法分配律进行简算;
(3)先算乘法,再运用加法结合律进行简算;
(4)先算小括号里的乘法,再算小括号里的减法,最后算括号外的除法。
【解答】解:(1)×÷
=÷
=
(2)÷7+×
=×+×
=(+)×
=1×
=
(3)+×+
=++
=+(+)
=+1
=1
(4)÷(﹣×)
=÷(﹣)
=÷
=
19.解方程。
x+3=9
【分析】方程的两边先同时减去3,然后两边同时除以。
【解答】解:x+3=9
x+3﹣3=9﹣3
x÷=6÷
x=9
四、操作。
20.在右面的空白处画一个半径是2cm的圆,并在圆中画一个圆心角是120°的扇形。
【分析】圆心确定圆的位置,半径确定圆的大小,由此以点O为圆心,以2厘米为半径,即可画出这个圆;因为圆周角为360°,所以用以圆的任意一条半径为扇形的边,再利用量角器画出圆心角为120°的扇形即可。
【解答】解:以点O为圆心,以2厘米为半径,解答如下:
21.根据下面的描述,在平面图上标出各场所的位置及路线图。
(1)体育馆在学校东偏北30°方向800m处。
(2)小青从学校出发,向正西方向走了400m后,再往西偏南40°的方向走了1.2km,到达少年宫。
【分析】(1)根据平面图上方向的辨别“上北下南,左西右东”,以学校的位置为观测点,即可确定体育馆的方向;根据体育馆与学校的实际距离及图中所标注的线段比例尺即可求出体育馆与学校的图上距离,从而在图标出体育馆的位置。
(2)同理,以学校的位置为观测点,即可确定小青拐弯点的方向、图上距离;以拐弯点的位置为观测点,即可确定少年宫的方向、图上距离,然后在图中标出少年宫的位置。
【解答】解:(1)800÷400=2(cm)
即体育馆在学校东偏北30°方向图上距离2cm处。
(2)400÷400=1(cm)
1.2km=1200m
1200÷400=3(cm)
即小青从学校出发,向正西方向走了图上距离1cm后,再往西偏南40°的方向走了图上距离3cm,到达少年宫。
根据以上信息画图如下:
五、统计。
22.以下是广东省和北京市在第七次全国人口普查中人口受教育情况的统计图。
根据统计图回答下面的问题。
(1)广东省与北京市相比, 北京市 拥有大学文化程度的人口所占百分比更高,占其人口总数的 45 %。
(2)在广东省,平均每100人中有 18 人拥有大学文化程度。
(3)下面的说法正确吗?正确的在括号里打“√”,错误的打“×”。
①两个统计图都是把全国人口总数看作单位“1”。 × (判断对错)
②北京市拥有大学文化程度的人口数一定比广东省拥有的人口数多。 × (判断对错)
【分析】(1)通过观察统计图可知,广东省与北京市相比,北京市拥有大学文化程度的人口所占百分比更高,占其人口总数的45%。
(2)在广东省,平均每100人中有18人拥有大学文化程度。
(3)①两幅统计图分别是把广东省人口总数看作单位“1”、北京市人口总数看作单位“1”。据此判断。
②虽然北京市拥有大学文化程度的人口数所占百分比高于广东省拥有大学文化程度的人口数所占的部分比,但是北京市和广东省的总人口不相同,广东省的人口总数大于北京市的人口总数,因此,北京市拥有大学文化程度的人口数不一定比广东省拥有的人口数多。据此解答。
【解答】解:广东省与北京市相比,北京市拥有大学文化程度的人口所占百分比更高,占其人口总数的45%。
(2)在广东省,平均每100人中有18人拥有大学文化程度。
(3)①两个统计图都是把全国人口总数看作单位“1”。此结论是错误的。
②北京市拥有大学文化程度的人口数一定比广东省拥有的人口数多。此结论是错误的。
故答案为:北京市,45;18;×,×。
23.下面的数据,分别用哪种统计图表示最合适?请把正确答案的序号填在括号里。
①扇形
②条形
③折线
(1)某班学生各身高段人数占全班人数的百分比情况。
用 ① 统计图
(2)小琪2019﹣2021年的身高变化情况。
用 ③ 统计图
(3)某学习小组三名同学的身高情况。
用 ② 统计图
【分析】分析题意,需明确条形统计图能很容易看出数量的多少;
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
扇形统计图能反映部分与整体的关系,由此根据情况选择即可。
【解答】解:(1)某班学生各身高段人数占全班人数的百分比情况。
用扇形统计图
(2)小琪2019﹣2021年的身高变化情况。
用折线统计图
(3)某学习小组三名同学的身高情况。
用条形统计图
故答案为:①,③,②。
六、只列式,不计算。
24.只列式,不计算。
【分析】观察图可知:把航模组的总人数看成单位“1”,它的是男生的人数18人,用18人除以,就是航模组的总人数。
【解答】解:18÷=27(人)
答:航模小组有27人。
25.一块长方形地,宽是40m,长是宽的,这块长方形地的面积是多少平方米?
【分析】首先根据求一个数的几分之几是多少,用乘法求出长,再根据长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:40×=50(米)
50×40=2000(平方米)
答:这块垂线地的面积是2000平方米。
26.牛郎星的运行速度是每秒26千米,织女星的运行速度是每秒14千米,织女星的运行速度比牛郎星慢百分之几?
【分析】先求出织女星的运行速度比牛郎星慢速度差,用速度差除以牛郎星的速度,即可得出织女星的运行速度比牛郎星慢百分之几。
【解答】解:(26﹣14)÷26
=12÷26
≈46%
答:织女星的运行速度比牛郎星慢46%。
七、解决问题。
27.学校篮球小组有学生50人,昨天有2人请假。篮球小组昨天的出勤率是多少?
【分析】出勤率是指出勤人数占总人数的百分比,计算方法是:出勤率=×100%。
【解答】解:×100%=96%
答:篮球小组昨天的出勤率是96%。
故答案为:96%。
28.张叔叔开车从广州到深圳办事,已经行驶了全程的,还需行驶100千米才到办事地点。张叔叔从广州到深圳一共要行驶多少千米?
【分析】把从广州到深圳一共要行驶的路程看成单位“1”,已经行驶了全程的,那么还剩下全程的(1﹣),它对应的数量是100千米,根据分数除法的意义,用100千米除以(1﹣)即可求出全程。
【解答】解:100÷(1﹣)
=100÷
=140(千米)
答:张叔叔从广州到深圳一共要行驶140千米。
29.目前世界上最高的鸟是鸵鸟,最高的哺乳动物是长颈鹿。如图,这只长颈鹿的身高是多少厘米?
【分析】把鸵鸟的身高看作单位“1”,则长颈鹿的身高是鸵鸟的(1+),根据分数乘法的意义,用鸵鸟的身高乘(1+)就是长颈鹿的身高。
【解答】解:250×(1+)
=250×
=550(厘米)
答:这只长颈鹿的身高是550厘米。
30.张大爷家有一块面积为150m2的菜地,准备种上萝卜和青菜。萝卜地和青菜地的面积比是3:2,这两块地的面积分别是多少平方米?
【分析】把这块菜地的面积平均分成(3+2)份,先用除法求出1份的面积,再用乘法分别求出3份(种萝卜)、2份(种青菜)的面积。
【解答】解:150÷(3+2)
=150÷5
=30(0m2)
30×3=90(0m2)
30×2=60(m2)
答:这两块地的面积一块是90平方米,一块是60平方米。
31.一个运动场(如图),两端是半圆形,中间是长方形。
(1)沿着这个运动场跑1圈,要跑多少米?
(2)给这个运动场铺上草坪,一共要铺多少平方米?
【分析】(1)根据圆的周长公式:C=πd,把数据代入公式求出两个弯道的长,再加上两条直道的长即可。
(2)根据圆的面积公式:S=πr2,长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:(1)3.14×60+100×2
=188.4+200
=388.4(米)
答:要跑388.4米。
(2)3.14×(60÷2)2+100×60
=3.14×900×6000
=2826+6000
=8826(平方米)
答:一共要铺8826平方米。× ÷
10× 10+
﹣=
30×30%=
×=
1÷5+=
÷6=
×1.8=
÷=
(+)×36=
×÷
÷7+×
+×+
÷(﹣×)
身高段/cm
140﹣149
150﹣159
160﹣170
占全班人数的百分比
15%
50%
35%
年份
2019
2020
2021
身高/cm
145
155
160
姓名
小华
小晴
小琪
身高/cm
153
150
160
× > ÷
10× < 10+
×>÷
10×<10+
﹣=
30×30%=
×=
1÷5+=
÷6=
×1.8=
÷=
(+)×36=
﹣=
30×30%=9
×=
1÷5+=1
÷6=
×1.8=0.4
÷=
(+)×36=31
×÷
÷7+×
+×+
÷(﹣×)
身高段/cm
140﹣149
150﹣159
160﹣170
占全班人数的百分比
15%
50%
35%
年份
2019
2020
2021
身高/cm
145
155
160
姓名
小华
小晴
小琪
身高/cm
153
150
160
身高段/cm
140﹣149
150﹣159
160﹣170
占全班人数的百分比
15%
50%
35%
年份
2019
2020
2021
身高/cm
145
155
160
姓名
小华
小晴
小琪
身高/cm
153
150
160
广东省广州市海珠区实验小学2021-2022学年六年级上学期第二次月考数学试卷: 这是一份广东省广州市海珠区实验小学2021-2022学年六年级上学期第二次月考数学试卷,共10页。试卷主要包含了填空题,判断题,选择题,计算题,操作题,解决问题等内容,欢迎下载使用。
广东省广州市海珠区新港路小学2021-2022学年六年级上学期第二次月考数学试卷: 这是一份广东省广州市海珠区新港路小学2021-2022学年六年级上学期第二次月考数学试卷,共4页。
广东省广州市海珠区实验小学教育集团2021-2022学年六年级上学期第二次月考数学试卷: 这是一份广东省广州市海珠区实验小学教育集团2021-2022学年六年级上学期第二次月考数学试卷,共4页。













