
所属成套资源:2025届高考数学一轮知识清单专题(解析版)
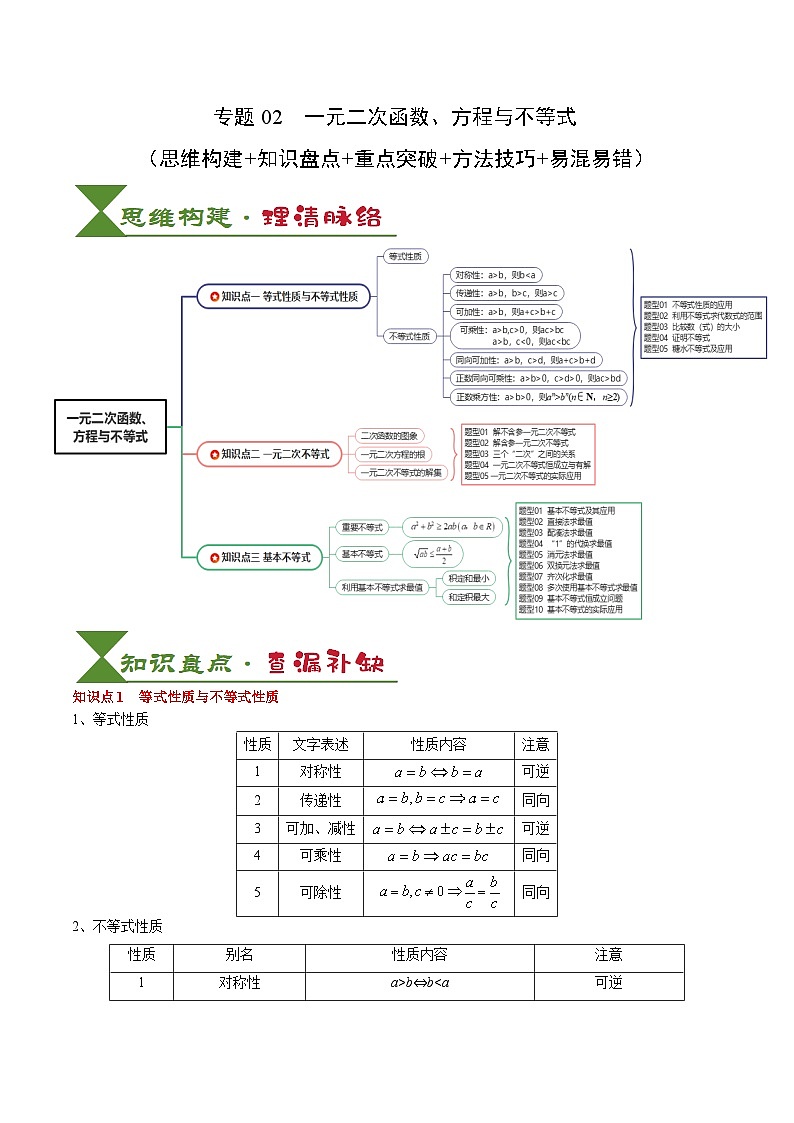
2025届高考数学一轮知识清单专题02 一元二次函数、方程与不等式(解析版)
展开
这是一份2025届高考数学一轮知识清单专题02 一元二次函数、方程与不等式(解析版),共20页。学案主要包含了直接法,配凑法,代换法,消元法,构造不等式法等内容,欢迎下载使用。
知识点1 等式性质与不等式性质
1、等式性质
2、不等式性质
知识点2 一元二次不等式的解集
知识点3 基本不等式
1、重要不等式:,(当且仅当时取号).
变形公式:
2、基本不等式:
(1)基本不等式成立的条件:
(2)等号成立的条件:当且仅当时取等号.
(3)算术平均数与几何平均数
设a>0,b>0,则a,b的算术平均数为,几何平均数为,
基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数.
3、利用基本不等式求最值
已知x>0,y>0,则
(1)如果积xy是定值p,那么当且仅当x=y时,x+y有最小值2eq \r(p).(简记:积定和最小)
(2)如果和x+y是定值p,那么当且仅当x=y时,xy有最大值eq \f(p2,4).(简记:和定积最大)
重难点01 利用基本不等式求最值的方法
法一、直接法:条件和问题间存在基本不等式的关系
【典例1】(2024·重庆·模拟预测)若实数,满足, 则 的最小值为( )
A.2B.C.4D.
【答案】D
【解析】,
当且仅当时,等号成立.故选:D.
【典例2】(2024·四川成都·三模)若正实数满足,则的最大值为( )
A.B.C.D.
【答案】A
【解析】因为,,
所以,即,
当且仅当时等号成立,
所以的最大值为.故选:A.
法二、配凑法:凑出“和为定值”或“积为定值”,直接使用基本不等式。
【典例1】(23-24高三下·河南·开学考试)已知,则的最小值为( )
A.6B.5C.4D.3
【答案】D
【解析】由于,所以,
由,
(当且仅当时取等号),可得的最小值为3,故选:D.
【典例2】(23-24高三上·山西晋中·开学考试)已知,则的最大值为( )
A.2B.4C.5D.6
【答案】B
【解析】因为,
所以,
当且仅当时取等号,因为,解得,故选:B
法三、代换法:代换法适用于条件最值中,出现分式的情况
类型1:分母为单项式,利用“1”的代换运算,也称乘“1”法;
【典例1】(23-24高三下·江苏镇江·开学考试)已知正数满足,则的最小值为( )
A.6B.7C.8D.9
【答案】D
【解析】因为正数满足,
所以,
当且仅当,即、时取等号.故选:D
【典例2】(23-24高三上·甘肃武威·期末)若,且,则的最小值为( )
A.6B.9C.4D.8
【答案】B
【解析】因为,所以,
因为,
当且仅当,即时,等号成立,
所以的最小值为9,故选:B.
类型2:分母为多项式时
方法1:观察法 适合与简单型,可以让两个分母相加看是否与给的分子型成倍数关系;
方法2:待定系数法,适用于所有的形式,
如分母为与,分子为,
设
∴,解得:
【典例1】(23-24高三下·江苏扬州·开学考试)已知实数,,满足,则的最小值为( )
A.B.C.D.
【答案】B
【解析】实数,,由,得,
因此,
当且仅当,即时取等号,
所以的最小值为.故选:B
【典例2】(2024·四川成都·模拟预测)若是正实数,且,则的最小值为( )
A.B.C.D.
【答案】A
【解析】因为
,
当且仅当时取等号,所以的最小值为.故选:A
法四、消元法:当题目中的变元比较多的时候,可以考虑削减变元,转化为双变量或者单变量问题。
【典例1】(2024·浙江嘉兴·二模)若正数满足,则的最小值是( )
A.B.C.D.2
【答案】A
【解析】由可得,
,
当且仅当,即时,等号成立,此时符合题意.
所以的最小值为.故选:A.
【典例2】(2024高三·全国·专题练习)已知实数满足,则的最小值是( )
A.B.C.D.
【答案】B
【解析】因为实数满足,所以,
则,
当且仅当,即时,等号成立,
所以的最小值是的最小值是,故选:B
法五、构造不等式法:寻找条件和问题之间的关系,通过重新分配,使用基本不等式得到含有问题代数式的不等式,通过解不等式得出范围,从而求得最值。
【典例1】(2023·山东潍坊·模拟预测)若正数满足,则的取值范围是( )
A.B.C.D.
【答案】A
【解析】由题意知为正数,且,
所以,化简得,解得,
当且仅当时取等号,所以,故A正确.故选:A.
【典例2】(23-24高三下·重庆·月考)对于正数,有,则的取值范围是( )
A.B.C.D.
【答案】C
【解析】由题可知:,
因为都是正数,所以(当且仅当时取等),
所以(当且仅当时取等),
化简可得,解得,故C正确.故选:C.
重难点02 不等式恒成立与能成立问题
一般利用参变分离法求解函数不等式恒(能)成立,可根据以下原则进行求解:
1、,
2、,
3、,
4、,
【典例1】(23-24高一上·辽宁·月考)若两个正实数x,y满足,且不等式恒成立,则实数m的取值范围为( )
A.B.或
C.D.或
【答案】A
【解析】由题意知,,
当且仅当,即时取等,
又不等式恒成立,
则不等式,解得,
所以实数m的取值范围为.故选:A.
【典例2】(23-24高三上·浙江宁波·期末)设实数x,y满足,,不等式恒成立,则实数k的最大值为( )
A.12B.24C.D.
【答案】B
【解析】,,变形为,
令,
则转化为,即,
其中
当且仅当,即时取等号,可知.故选:B
重难点03 求含参数的一元二次不等式
对求含参的不等式,应对参数进行分类讨论,常见的分类有:
(1)根据二次项系数为正、负及零进行分类;
(2)根据判别式与0的关系判断根的个数;
(3)有两个根式,有时还需根据两根的大小进行讨论。
【典例1】(23-24高三上·浙江绍兴·期末)(多选)已知,关于x的一元二次不等式的解集可能是( )
A.或B.
C.D.
【答案】ACD
【解析】当时,;
当时,或,故A正确;
当时,,
若,则解集为空集;
若,则不等式的解为:,故D正确;
若,则不等式的解为:,故C正确.故选:ACD
【典例2】(2024高三·全国·专题练习)(1)解关于实数的不等式:.
(2)解关于实数的不等式:.
【答案】(1)答案见解析;(2)答案见解析;
【解析】(1)易知方程的,
由得,解得,
当时,的解集为,
当时,的解集为,
当时,的解集为.
(2)对方程,
当时,即时,不等式的解集为
当时,即或时,
的根为,
不等式的解集为;
综上可得,时,不等式的解集为,
或时,不等式的解集为.
一、比较两数(式)的大小
1、作差法:
(1)原理:设,则;;;
(2)步骤:作差并变形判断差与0的大小得出结论。
(3)注意:利用通分、因式分解、配方等方法向有利于判断差的符号的方向变形。
2、作商法:
(1)原理:设,则;;
(2)步骤:作商并变形判断商与1的大小得出结论。
(3)注意:作商时各式的符号应相同,如果均小于0,所得结果与“原理”中的结论相反,变形方法有分母(分子)有理化,指、对数恒等变形。
【典例1】(22-23高三·全国·对口高考)(1)比较与的大小;
(2)已知,比较与大小
【答案】(1);(2)
【解析】(1)因为,所以,
所以①当时,,所以,
②当时,,即,所以,
③当时,,即,所以,
综上所述:当,.
(2),
因为,所以,所以,
由,
所以,所以,即,
故.
【典例2】(2024高三·全国·专题练习)已知均为正实数,且.
(1)比较与的大小;
(2)比较和的大小.
【答案】(1);(2)答案见解析
【解析】(1),
均为正实数,,
;
(2)当时,函数为增函数;当时,函数为减函数.
①当时,,则,
若,则;
若,则;
②当时,;
③当时,,则,
若,则;
若,则.
综上所述,当或时,;
当时,;
当或时,.
二、利用不等式的性质求数(式)的范围
已知,,求的取值范围
第一步:设;
第二步:经过恒等变形,求得待定系数;
第三步:再根据不等式的同向可加性即可求得的取值范围。
【典例1】(23-24高三上·河南洛阳·月考)(多选)已知,,则下列选项中正确的有( )
A.B.C.D.
【答案】AB
【解析】由,可得,又,所以,故A正确;
由,可得,又,所以,故B正确;
由,可得,又,
所以,因为,所以,故C错误;
由,,得,,
所以,所以,故D错误.故选:AB
【典例2】(23-24高一上·山西太原·月考)已知,,则的取值范围( )
A.B.C.D.
【答案】D
【解析】由题意,,故,即.故选:D
三、解一元二次不等式的步骤
第一步:先看二次项系数是否为正,若为负,则将二次项系数化为正数;
第二步:写出相应的方程,计算判别式:
①时,求出两根,且(注意灵活运用因式分解和配方法);
②时,求根;
③时,方程无解
第三步:根据不等式,写出解集.
【典例1】(23-24高三下·河北沧州·月考)已知集合,则( )
A.B.C.D.
【答案】B
【解析】,所以,故选:B
【典例2】(23-24高一上·四川成都·期中)一元二次不等式的解为,那么的解集为( )
A.B.
C.D.
【答案】D
【解析】一元二次不等式的解为,
所以的解为,且,
由韦达定理得,
代入得,故选:D.
四、一元二次不等式恒成立问题
恒成立问题求参数的范围的解题策略:
(1)弄清楚自变量、参数。一般情况下,求谁的范围,谁就是参数;
(2)一元二次不等式在R上恒成立,可用判别式;一元二次不等式在给定区间上恒成立,不能用判别式,一般分离参数求最值或分类讨论。
【典例1】(23-24高三下·上海浦东新·月考)若关于的不等式的解集为,则实数的取值范围是 .
【答案】
【解析】当时,不等式为,显然不符合题意;
当时,因为关于的不等式的解集为,
所以有,
所以实数的取值范围是.
【典例2】(2024·陕西西安·模拟预测)当时,不等式恒成立,则实数的取值范围是 .
【答案】.
【解析】当时,不等式恒成立,
所以当时,恒成立,则,
令,则在单调递增,
所以,所以.
五、基本不等式的实际应用
解实际应用题的三个注意点:
1、设变量时一般要把求最大值或最小值的变量定义为函数;
2、根据实际问题抽象很出有关式关系式后,只需利用基本不等式求得函数的最值;
3、在求函数的最值时,一定要在定义域(使实际问题有意义的自变量的取值范围)内求解。
【典例1】(2024·广东韶关·二模)在工程中估算平整一块矩形场地的工程量W(单位:平方米)的计算公式是,在不测量长和宽的情况下,若只知道这块矩形场地的面积是10000平方米,每平方米收费1元,请估算平整完这块场地所需的最少费用(单位:元)是( )
A.10000B.10480C.10816D.10818
【答案】C
【解析】设矩形场地的长为米,则宽为米,
,
当且仅当,即时,等号成立.
所以平整这块场地所需的最少费用为元.故选:C
【典例2】(2024·黑龙江·二模)“不以规矩,不能成方圆”出自《孟子·离娄章句上》.“规”指圆规,“矩”指由相互垂直的长短两条直尺构成的方尺,是古人用来测量、画圆和方形图案的工具,今有一块圆形木板,按图中数据,以“矩”量之,若将这块圆形木板截成一块四边形形状的木板,且这块四边形木板的一个内角满足,则这块四边形木板周长的最大值为( )
A.B.
C.D.
【答案】A
【解析】因为四边形木板的一个内角满足,如图,
设,由题设可得圆的直径为,
故,因,为三角形内角,故,
故,
故,
故,
故,当且仅当时等号成立,
同理,当且仅当等号成立,
故四边形周长的最大值为,故选:A.
六、利用不等的性质及基本不等式证明不等式
1、无附加条件的不等式证明:证明时要根据其结构特征,合理地构造并正确选用基本不等式或其变形形式,这也是证明轮换对称结构的不等式(把b换a,a换c,c换b后,代数式不变的式子叫做轮换对称性,其特征是a,b,c的地位一样)的常用思路。
2、有附加条件的不等式的证明:应先观察已知条件和所证不得呢公式之间的联系,当已知条件中含有“1”时,要注意“1”的代换。另外,解题时要时刻注意等号能否取到。
【典例1】(23-24高三下·陕西西安·月考)设为正数,且. 证明:
(1);
(2).
【答案】(1)证明见解析;(2)证明见解析
【解析】(1)由已知有,从而,
故,
当且仅当时等号成立.
(2)方法一:由已知条件,结合基本不等式即可得到
.
方法二:等价于,
根据题设有,
当且仅当时等号成立.
【典例2】(2024·青海·一模)已知正数满足.求证:
(1);
(2).
【答案】(1)证明见解析;(2)证明见解析
【解析】(1)证明:因为正数满足,
由,当且仅当时,等号成立,
可得,
即,所以,当且仅当时,等号成立.
(2)证明:由
,
当且仅当,即,等号成立.
所以.
易错点1 忽视不等式性质成立的条件
点拨:在使用不等式的基本性质进行推理论证时一定要注意前提条件,如不等式两端同时乘以或同时除以一个数、式,两个不等式相乘、一个不等式两端同时n次方时,一定要注意使其能够这样做的条件.
【典例1】(2024·北京丰台·二模)若,且,则( )
A.B.
C.D.
【答案】D
【解析】由于,取,,,
无法得到,,故AB错误,
取,则,无法得到,C错误,
由于,则,所以,故选:D
【典例2】(2024·陕西安康·模拟预测)若满足,则( )
A.B.
C.D.
【答案】C
【解析】由,得,所以,所以,所以错误;
令,此时与无意义,所以错误;
因为,所以由不等式的性质可得,所以正确;
令,则,所以错误.故选:.
易错点2 忽视基本不等式应用的条件
点拨:(1)利用基本不等式a+b≥2ab以及变式ab≤a+b22等求函数的最值时,务必注意a,b为正数(或a,b非负),特别要注意等号成立的条件.
(2)对形如y=ax+bx(a,b>0)的函数,在应用基本不等式求函数最值时,一定要注意ax,bx同号.
【典例1】(2022·黑龙江哈尔滨·三模)已知x,y都是正数,且,则下列选项不恒成立的是( )
A.B.
C.D.
【答案】D
【解析】x,y都是正数,由基本不等式,,,,
这三个不等式都是当且仅当时等号成立,而题中,
因此等号都取不到,所以ABC三个不等式恒成立;
中当且仅当时取等号,如即可取等号,D中不等式不恒成立.
故选:D.
【典例2】(2024高三·全国·专题练习)下列不等式证明过程正确的是( )
A.若,则
B.若x>0,y>0,则
C.若x<0,则
D.若x<0,则
【答案】D
【解析】∵可能为负数,如时,,∴A错误;
∵可能为负数,如时,,∴B错误;
∵,如时,,∴C错误;
∵,,,∴,
当且仅当,即等号成立,∴D正确.故选:D.
易错点3 连续使用均值不等式忽略等号能否同时成立
点拨:连续使用均值不等式求最值或范围,要注意判断每个等号成立的条件,检验等号能否同时成立.
【典例1】(2024·全国·模拟预测)已知,,且,则的最小值为 .
【答案】64
【解析】法一:因为,,所以,
当且仅当,即,时,等号成立,
所以,
当且仅当,即,时,等号成立.
所以的最小值为64.
法二:因为,,,
所以
,
当且仅当,即时,等号成立.
所以的最小值为64.
【典例2】(23-24高三下·浙江宁波·月考)已知正实数满足,则的最小值为 .
【答案】
【解析】任意的正实数,,,满足,
所以,
由于,为正实数,故由基本不等式得,
当且仅当,即,时,等号成立,
所以 ,
当且仅当,即时,等号成立,
综上,的最小值为16.
易错点4 解分数不等式忽略分母不为零
点拨:解含有分数的不等式,在去分母时要注意分母不为零的限制条件,防止出现增解,如
【典例1】(2024·山西朔州·一模)已知集合,则( )
A.B.C.D.
【答案】C
【解析】,故,故选:C.
【典例2】(23-24高三上·山东聊城·期中)设集合,,则( )
A.B.C.D.
【答案】D
【解析】由不等式,则等价于,解得,
所以,由,则.故选:D.性质
文字表述
性质内容
注意
1
对称性
可逆
2
传递性
同向
3
可加、减性
可逆
4
可乘性
同向
5
可除性
同向
性质
别名
性质内容
注意
1
对称性
a>b⇔bb,b>c⇒a>c
同向
3
可加性
a>b⇔a+c>b+c
可逆
4
可乘性
a>b,c>0⇒ac>bc
a>b,cd⇒a+c>b+d
同向
6
正数同向可乘性
a>b>0,c>d>0⇒ac>bd
同向
7
正数乘方性
a>b>0⇒an>bn(n∈N,n≥2)
同正
判别式Δ=b2-4ac
Δ>0
Δ=0
Δ0)的图象
方程ax2+bx+c=0
(a>0)的根
有两相异实根x1,x2(x10
(a>0)的解集
{x|xx2}
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠-\f(b,2a)))))
{x|x∈R}
ax2+bx+c0)的解集
{x|x1< x
相关学案
这是一份2025届高考数学一轮知识清单专题01 集合综合归类(解析版),共45页。学案主要包含了名师点睛等内容,欢迎下载使用。
这是一份2025届高考数学一轮知识清单专题02 常用逻辑用语归类 (解析版),共29页。学案主要包含了小问1详解,小问2详解,小问3详解等内容,欢迎下载使用。
这是一份2025届高考数学一轮知识清单专题03 均值不等式及不等式综合(解析版),共36页。









