江西省南昌民德学校2023-2024学年八年级上学期期中考试数学试卷(含答案)

这是一份江西省南昌民德学校2023-2024学年八年级上学期期中考试数学试卷(含答案)，共10页。试卷主要包含了1~13等内容，欢迎下载使用。

►上册11.1~13.3.1◄
说明：共有六个大题，23个小题，满分120分，作答时间120分钟.
注意事项：
1. 答题前，考生务必将密封线内的项目填写清楚.
2. 必须使用黑色签字笔书写，字体工整、笔迹清楚.
一、单项选择题（本大题共6小题，每小题3分，共18分）
在每小题列出的四个备选项中只有一项是最符合题目要求的，请将其代码填入题后括号内.错选、多选或未选均不得分.
1. 第19届亚运会于2023年9月23日至10月8日在杭州举办，下列关于体育运动的图标中，是轴对称图形的是（ ）
A. B. C. D.
2. 已知一个三角形三边的长分别为7，a，3，则a的值可能为（ ）
A. 2B. 4C. 8D. 10
3. 如果一个多边形的边数增加2，那么关于其内角和与外角和的变化，下列说法正确的是（ ）
A. 内角和、外角和均增加B. 外角和不变，内角和增加
C. 内角和不变，外角和增加D. 内角和、外角和均不变
4. 如图，已知，，要使，可添加的条件是（ ）
A. B. C. D.
5. 已知点与点关于y轴对称，则的值为（ ）
A. －7B. －1C. 1D. 7
6. 两个底角为、顶角为的等腰三角形，叫做“黄金三角形”，这种三角形既美观又标准.如图，在中，，，BD，CE为的角平分线，则图中“黄金三角形”的个数是（ ）
A. 1B. 4C. 5D. 6
二、填空题（本大题共6小题，每小题3分，共18分）
7. 在中，，则的度数为______.
8. 正n边形的一个内角为，则n的值是______.
9. 如图，这是由4个相同的小正方形组成的田字格，则的度数为______.
第9题图
10. 如图，P是的平分线AD上一点，过点P作于点E.若，则点P到AB的距离是______.
第10题图
11. 如图，在钝角中，CD是的平分线，CE是的高，若，，则的度数为______.
第11题图
12. 在平面直角坐标系中，点，点，点，若是以OA为直角边的等腰直角三角形，则点B的坐标为______.
三、解答题（本大题共5小题，每小题6分，共30分）
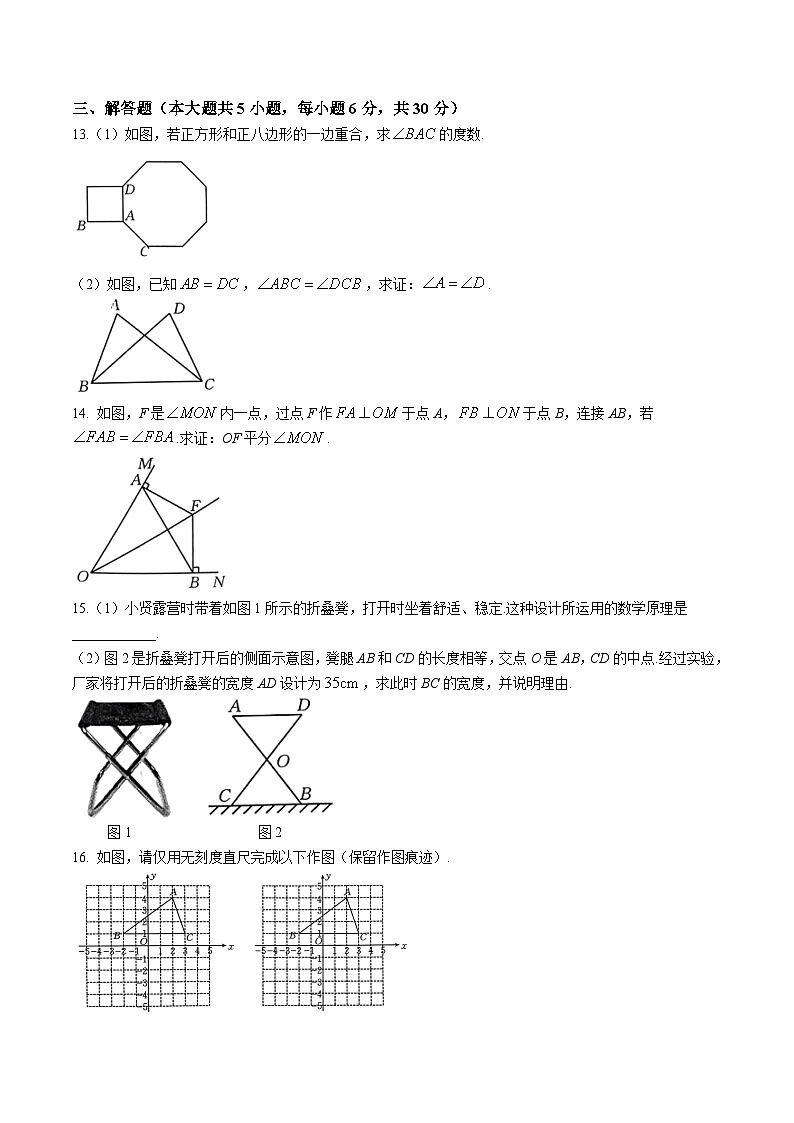
13.（1）如图，若正方形和正八边形的一边重合，求的度数.
（2）如图，已知，，求证：.
14. 如图，F是内一点，过点F作于点A，于点B，连接AB，若.求证：OF平分.
15.（1）小贤露营时带着如图1所示的折叠凳，打开时坐着舒适、稳定.这种设计所运用的数学原理是____________.
（2）图2是折叠凳打开后的侧面示意图，凳腿AB和CD的长度相等，交点O是AB，CD的中点.经过实验，厂家将打开后的折叠凳的宽度AD设计为，求此时BC的宽度，并说明理由.
图1 图2
16. 如图，请仅用无刻度直尺完成以下作图（保留作图痕迹）.
图1 图2
（1）在图1中作，使得与关于x轴对称.
（2）在图2中作AB边上的高CD.
17. 课本再现
如图，直线l垂直平分线段AB，，，，…是l上的点，分别量一量点，，，…到点A与点B的距离，你有什么发现？可以发现，点，，，…到点A的距离与它们到点B的距离分别相等.
定理证明
（1）为了证明该性质，珍珍画出了图形，并写出了“已知”和“求证”，请你完成证明过程.
已知：如图1，直线，垂足为C，，点P在直线l上，求证：.
知识应用
（2）如图2，在中，，DE，FG分别是边AB，AC的垂直平分线，与的交点分别为D，E，F，G，连接AD，AF，求的周长.
图1 图2
四、解答题（本大题共3小题，每小题8分，共24分）
18. 如图，与关于直线l对称，其中，，，.
（1）连接AD，写出线段AD与直线l的关系.
（2）求的度数.
（3）求的周长和的面积.
19. 如图，在正六边形ABCDEF中，M，N分别是边BC，CD上的点，且，AM与BN交于点Q.
（1）求证：；
（2）求的度数.
20. 如图，在四边形ABCD中，，连接对角线AC，E为CD的中点，连接AE并延长，交BC的延长线于点F，AF平分.
（1）求证：.
（2）判断AF与CD的位置关系，并说明理由.
五、解答题（本大题共2小题，每小题9分，共18分）
21. 如图1，CD是的高，.
图1 图2
（1）证明：是直角三角形.
（2）如图2，若AE是角平分线，AE与CD相交于点F.请判断是否为等腰三角形，并说明理由.
22. 阅读信息：
如图1，在中，，，D是外一点，且，求的度数.
解：设.
∵是等腰三角形，∴.
又∵，∴，∴.
同理，∵是等腰三角形，∴，
∴.
请根据阅读信息解决问题.
如图2，在中，，，D是外一点，且，求的度数.
图1 图2
六、解答题（本大题共12分）
23. 综合与实践
问题提出
如图1，在中，AD平分，交BC于点D，且，则AB，CD，AC之间存在怎样的数量关系？并说明理由.
方法运用
（1）我们可以通过作辅助线，构造全等三角形来解题.如图2，延长AC至点E，使得，连接DE，……，请判断AB，CD，AC之间的数量关系并补充完整解题过程.
（2）以上方法叫做“补短法”.我们还可以采用“截长法”，即通过在AB上截取线段构造全等三角形来解题.如图3，在线段AB上截取AF，使得①______，连接②______.请补全空格，并在图3中画出辅助线.
延伸探究
（3）小明发现“补短法”或“截长法”还可以帮助我们解决其他多边形中的问题.如图4，在五边形ABCDE中，，，，若，求的度数.
图1 图2 图3 图4
2023~2024学年度八年级上学期期中综合评估
数学参考答案
1. A 2. C 3. B 4. D 5. D 6. C
7. 8. 5 9. 10. 12 11. 12. 或或
13.（1）解：∵正八边形每个内角的度数是，
∴……1分
∵,
∴.……3分
（2）证明：在和中，
，
∴，
∴.……3分
14. 证明：∵，
∴.……2分
∵，，
∴点F在的平分线上，
∴OF平分.……6分
15. 解：（1）三角形具有稳定性.……2分
（2）.……3分
理由：∵O是AB，CD的中点，
∴，.
在和中，
，
∴，……5分
∴.
又∵，
∴.……6分
16. 解：（1）如图1，为所求.……3分
（2）如图2，线段CD为所求.……6分
图1 图2
17. 解：（1）证明：∵直线，
∴.……1分
又∵，，
∴，
∴.……3分
（2）∵DE，FG分别是边AB，AC的垂直平分线，
∴，，
∴的周长.……6分
18. 解：（1）直线l垂直平分AD.……2分
（2）∵与关于直线l对称，
∴，
∴.……4分
（3）∵，，，，
∴，，，
∴的周长，……6分
的面积.……8分
19. 解：（1）证明：∵六边形ABCDEF为正六边形，
∴，.……1分
∵，
∴，即.……2分
在和中，
，
∴.……4分
（2）∵，
∴.……5分
已知，
∴，
∴.……8分
20. 解：（1）证明：∵，
∴.……1分
∵AF平分，∴，
∴，∴.……4分
（2）.……5分
（方法不唯一）理由：∵E为CD的中点，
∴.
在和中，
，
∴，
∴.……7分
又∵，∴（三线合一）.……8分
21. 解：（1）证明：∵CD是的高，
∴，
∴.……1分
∵，
∴，……3分
∴是直角三角形.……4分
（2）是等腰三角形.……5分
理由：∵AE是角平分线，∴.
∵，
∴在中，，在中，，
∴.……7分
∵，∴，
∴，∴是等腰三角形.……9分
22. 解：设.……1分
∵，∴是等腰三角形，∴.……3分
又∵，……4分
∴，即.……6分
∵，∴是等腰三角形，
∴，……7分
∴.……9分
23. 解：（1）.……1分
理由：∵AD平分，∴.
又∵，，
∴，∴.……2分
∵，∴.
又∵，
∴，∴.……3分
∵，∴.……5分
（2）①AC ②DF.……7分
辅助线如图1所示.……8分
图1 图2
（3）如图2，延长BA至点G，使，连接BE，GE.
∵，，
∴.……9分
∵，，，
∴，
∴，.
∵，
∴.……10分
又∵，，
∴，
∴.……11分
又∵，
∴.……12分