山东省烟台市蓬莱区2024届九年级下学期中考二模数学试卷(含答案)

这是一份山东省烟台市蓬莱区2024届九年级下学期中考二模数学试卷(含答案)，共15页。

注意事项：
1．本试卷共8页，共120分；考试时间120分钟．考试结束后，请将答题卡上交．
2．答题前，务必用0.5毫米黑色的签字笔将自己的姓名、准考证号、座位号填写在试卷和答题卡规定的位置上．
3．选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．
4．非选择题必须用0.5毫米黑色签字笔作答，答案必须写在答题卡指定区域内相应的位置；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带．
5．写在试卷上或答题卡指定区域外的答案无效．
一、选择题（本题共10个小题，每小题3分，满分30分）每小题都给出标号为A，B，C，D四个备选答案，其中有且只有一个是正确的．
1．下列各数为无理数的是（ ）
A．B．C．0.618D．
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
3．如图是由6个相同的正方体组成的立体图形，它的俯视图是（ ）
A．B．C．D．
4．下列运算正确的是（ ）
A．B．C．D．
5．实数a，b，c在数轴上的对应点的位置如图所示，则正确的结论是（ ）
A．B．C．D．
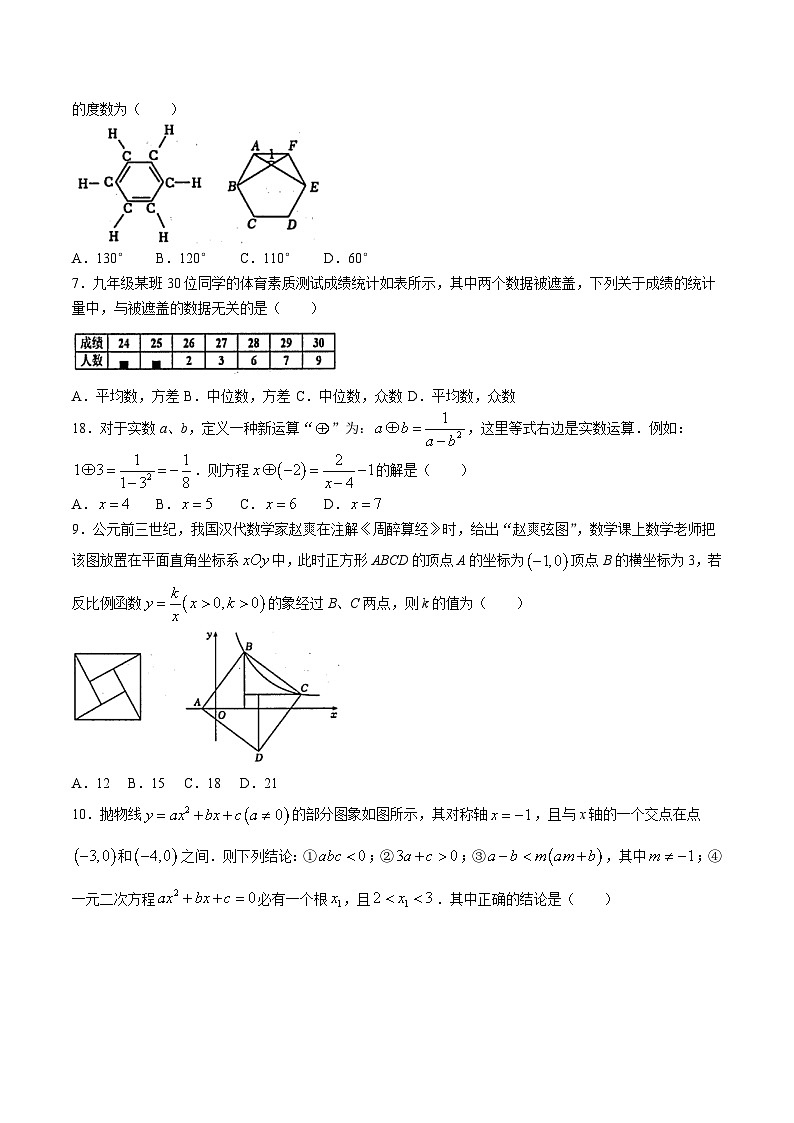
6．苯分子的环状结构是由德国化学家凯库勒提出的．随着研究的不断深入，发现苯分子中的6个碳原子与6个氢原子均在同一平面，且所有碳碳键的键长都相等（如图1）（正六边形），图2是其平面示意图，则的度数为（ ）
A．130°B．120°C．110°D．60°
7．九年级某班30位同学的体育素质测试成绩统计如表所示，其中两个数据被遮盖，下列关于成绩的统计量中，与被遮盖的数据无关的是（ ）
A．平均数，方差B．中位数，方差C．中位数，众数D．平均数，众数
18．对于实数a、b，定义一种新运算“”为：，这里等式右边是实数运算．例如：．则方程的解是（ ）
A．B．C．D．
9．公元前三世纪，我国汉代数学家赵爽在注解《周醉算经》时，给出“赵爽弦图”，数学课上数学老师把该图放置在平面直角坐标系中，此时正方形ABCD的顶点A的坐标为顶点B的横坐标为3，若反比例函数的象经过B、C两点，则k的值为（ ）
A．12B．15C．18D．21
10．抛物线的部分图象如图所示，其对称轴，且与x轴的一个交点在点和之间．则下列结论：①；②；③，其中；④一元二次方程必有一个根，且．其中正确的结论是（ ）
A．①②B．①③C．②④D．③④
二、填空题（本大题共6个小题，每小题3分，满分18分）
11．2024年山东省普通高考报名考生共977560人，977560用科学记数法表示为______．
12．已知关于x的方程有两个不相等的实数根，则m的取值范围是______．
13．在平面直角坐标系中，点是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，则点P的对应点的坐标为______．
14．如图，Rt△ABC中，，利用尺规在BC，BA上分别截取BE，BD，使；分别以D，E为圆心、以大于的长为半径作弧，两弧在内交于点F；作射线BF，点P，G分别为射线BF，线段BC上的动点，若，，则的最小值为______．
15．如图，在矩形ABCD中，，，，以AB长为半径画弧，交AD的延长线于点E，以CB长为半径画弧，交CD于点H，两弧交于点B，则图中形成的阴影部分的面积是______．
16．如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则为______．
三、解答题（本大题共8个小题，满分72分）
17．（本题满分6分）
先化简，再求值：，其中．
18．（本题满分7分）
“机动车行驶到斑马线要礼让行人”等交通法规实施后，某校数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生，调查结果分为四种：A．非常了解，B．比较了解，C．基本了解，D．不太了解，实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图．
请结合图中所给信息解答下列问题：
（1）本次共调查______名学生；扇形统计图中C所对应扇形的圆心角度数是______。
（2）补全条形统计图；
（3）该校共有800名学生，根据以上信息，请你估计全校学生中对这些交通法规“非常了解”的有多少名？
（4）通过此次调查，数学课外实践小组的学生对交通法规有了更多的认识，学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛，请用列表或画树状图的方法求甲和乙两名学生同时被选中的概率．
19．（本题满分6分）
如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为，，．
（1）将△ABC先向左平移6个单位，再向上平移4个单位，得到，画出两次平移后的，并写出点的坐标；
（2）画出绕点顺时针旋转90°后得到，并写出点的坐标；
（3）在（2）的条件下，求点旋转到点的过程中所经过的路径长（结果保留）．
20．（本小题满分7分）
某大型购物中心为方便顾客地铁换乘，准备在底层至层之间安装电梯，截面图如图所示，底层与层平行，层高AD为9米，A、B间的距离为5.2米，．
（1）请问身高1.9米的人在竖直站立的情况下搭乘电梯，在B处会不会碰到头？请说明理由．
（2）若采取中段平台设计（如图虚线所示）．已知平台，且AE段和FC段的坡度，求平台EF的长度．
21．（本题满分8分）
如图，四边形ABCD中，，点O为对角线BD的中点，过点O的直线l分别与AD、BC所在的直线相交于点E、F．（点E不与点D重合）
（1）求证：；
（2）当直线时，连结BE、DF，试判断四边形EBFD的形状，并说明理由．
22．（本题满分7分）
为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台，假定该设备的年销售量y（单位：台）和销售单价x（单位：万元）成一次函数关系．
（1）求年销售量y与销售单价x的函数关系式；
（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？
23．（本题满分9分）
如图，在△ABC中，，D是BC中点．
（1）尺规作图：以AC为直径作⊙O，交AB于点E（保留作图痕迹，不需写作法）；
（2）求证：DE是⊙O的切线；
（3）若，，求O到CE的距离．
24．（本题满分10分）
已知△ABC和△ADE都是等腰三角形，，，，且，连接EC，且，直线BC交直线DE于点F．
（1）如图1，猜想BF与DE的位置关系，并说明理由；
（2）如图2，依次取CE、AC的中点M、N，连接FM、MN，求证：；
（3）如图3，在（2）的条件下，连接FN，若，在将△AEC绕点A旋转的过程中，请直接写出线段FN的最大值．
25．（本题满分12分）
如图1，在平面直角坐标系中，已知二次函数的图象与x轴交于点，，与y轴交于点C．
（1）求抛物线的解析式；
（2）已知E为抛物线上一点，F为抛物线对称轴l上一点，以B，E，F为顶点的三角形是等腰直角三角形，且，求出点F的坐标；
（3）如图2，P为第一象限内抛物线上一点，连接AP交y轴于点M，连接BP并延长交y轴于点N，在点P运动过程中，是否为定值？若是，求出这个定值；若不是，请说明理由．
2024年数学二模试题参考答案及评分意见
一、选择题（本题共10个小题，每小题3分，满分30分）
二、填空题（本大题共6个小题，每小题3分，满分18分）
11．12．且13．或
14．15．16．
三、解答题（本大题共7个小题，满分72分）
17．（本题满分6分）
解：
．
原式．
18．（本题满分7分）
（1）60、90°
（2）D类型人数为，则B类型人数为，
补全条形图如下：
（3）估计全校学生中对这些交通法规“非常了解”的有名；
（4）画树状图为：
开始共有12种等可能的结果数，其中甲和乙两名学生同时被选中的结果数为2，所以甲和乙两名学生同时被选中的概率为．
19．（本题满分6分）
（1）解：如图所示即为所求，；
（2）如图所示即为所求，；
（3），
点旋转到点所经过的路径长为．
20．（本题满分7分）
（1）解：会碰到头部
连接AB，过点B作，交AC于点G，
，，
，
，
会碰到头部；
（2）解：，
，
过点F作，垂足为点M，过点E作，垂足为点N，
设，则，
段和FC段的坡度，
，，
，
（米）．
答：平台EF的长度为7米．
21．（本题满分8分）
（1）证明：，
，
∵点O为对角线BD的中点，
，
在△DOE和△BOF中，
，
．
（2）解：四边形EBFD是菱形，理由如下：
，直线l经过点O且，
直线l是线段BD的垂直平分线，
，，
，，
，
四边形EBFD是菱形．
22．（本题满分7分）
解：（1）设年销售量y与销售单价x的函数关系式为，
将、代入，得：
，
解得：，
年销售量y与销售单价x的函数关系式为．
（2）设此设备的销售单价为x万元/台，则每台设备的利润为万元，销售数量为台，
根据题意得：，
整理，得：，
解得：，．
此设备的销售单价不得高于70万元，
．
答：该设备的销售单价应是50万元/台．
23．（本题满分9分）
（1）解：⊙O如图所示；
（2）证明：连接OE、CE，
AC为直径，
，
∵D为边中点，
∴DE为Rt△BEC斜边BC上的中线，
，
，
，
，
，
，
OE是半径，
DE是⊙O的切线；
（3）解：作于F，
由垂径定理得F是弦的中点，
∴OF是△ACE的中位线，
，
，
，
，即，
，
，
O到的距离为．
24．（本题满分10分）
（1）解：，
，，
，，
，
，
又，
，
，
，
又，
，
，
．
（2）解：，
，
又∵M是CE的中点，
,
CE、AC的中点分别是M、N，
，
．
（3）．
25．（本题满分12分）
解：（1）将点，，代入得：
，
解得：，
抛物线解析式为；
（2）点，，
抛物线的对称轴为直线，
设直线l与x轴交于点G，过点E作于点D，
当F在x轴上方时，如图：
以B，E，F为顶点的三角形是等腰直角三角形，且，
，
，，
，
，，
设，则，，
，
E点在抛物线上，
，
解得：（舍去）或，
；
当F在x轴下方时，如图：
同理可得，，，
设，则，
把代入得：
，
解得（舍去）或，
；
当E点与A点重合时，如图所示，
，△ABF是等腰直角三角形，且，
，
此时，
由对称性可得，点也满足条件，
综上所述，或或或；
（3）为定值6，理由如下：
设，直线AP的解析式为，BP的解析式为，
点，，，
∴，，
解得：，，
直线AP的解析式为，BP的解析式为，
在中，令得，
，
在中，令得，
，
在抛物线上，
，
，
为定值6．题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
C
D
D
B
C
B
C
B