中职高教版（2021）1.1 充分条件和必要条件获奖ppt课件

这是一份中职高教版（2021）1.1 充分条件和必要条件获奖ppt课件，共22页。PPT课件主要包含了学习目标，创设情境生成问题，调动思维探究新知，探究与发现，温馨提示，巩固知识典型练习，巩固知识典例练习，巩固练习提升素养，课堂小结，数学是符号加逻辑等内容，欢迎下载使用。

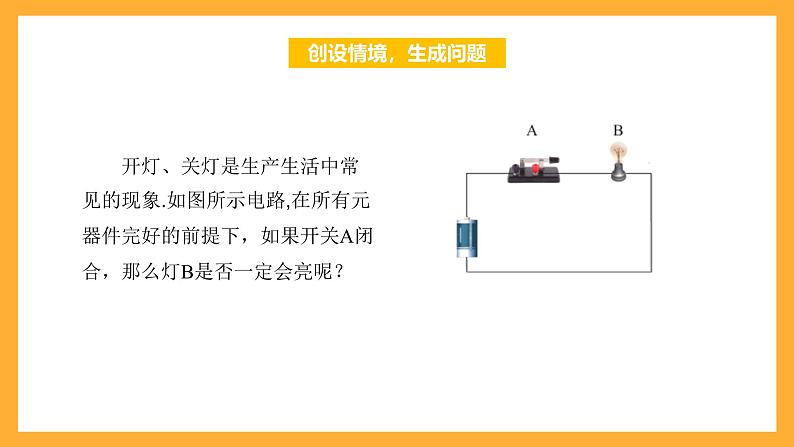
开灯、关灯是生产生活中常见的现象.如图所示电路,在所有元器件完好的前提下，如果开关A闭合，那么灯B是否一定会亮呢？
能判断真假的陈述句称为命题.判断为真的命题称为真命题，判断为假的命题称为假命题.
一般地, 对于形如“如果p,那么q”的命题, 我们称p为命题的条件, 简称条件; 称q为命题的结论，简称结论．
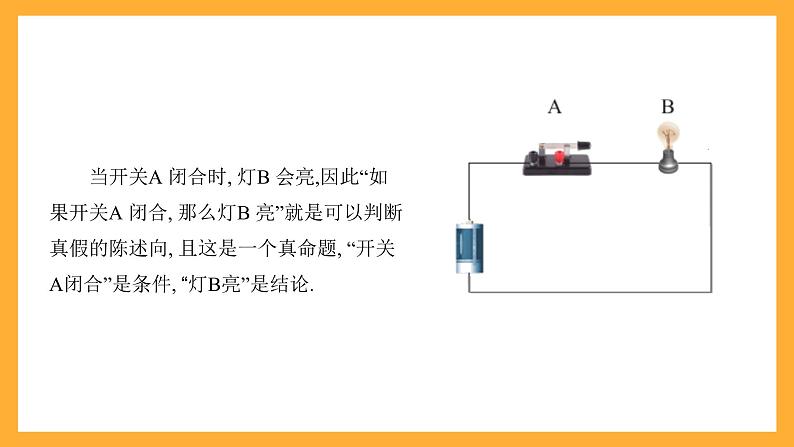
当开关A 闭合时, 灯B 会亮,因此“如果开关A 闭合, 那么灯B 亮”就是可以判断真假的陈述向, 且这是一个真命题, “开关A闭合”是条件, “灯B亮”是结论.
一般地，若命题“如果p，那么q”是真命题，即由p可以推出q，则称p是q的充分条件，记作p⇒q.
若命题“如果p，那么q”是假命题，即由p不能推出q，则称p不是q的充分条件，记作p⇏q.
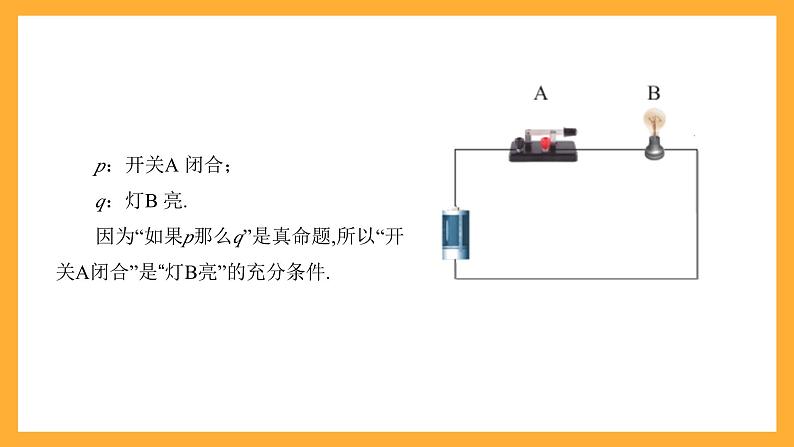
p：开关A 闭合； q：灯B 亮. 因为“如果p那么q”是真命题,所以“开关A闭合”是“灯B亮”的充分条件.
函数型计算器的标准设置中, 已知正弦函数值,只能显示-90°~90°范围内的角． 函数型计算器的标准设置中, 已知余弦函数值, 只能显示0°~180°范围内的角． 函数型计算器的标准设置中, 已知正切函数值, 只能显示 -90°~90°范围内的角．
典例1 指出下列命题的条件p和结论q，并判断p是否为q的充分条件. (1)如果x是整数，那么x是有理数； (2)如果a=0，那么ab=0； (3)第一象限角都是锐角.
解 (1)条件p:x是整数;结论q: 是有理数.因为当x 是整数时,  x一定是有理数，所以此命题是真命题，p是q的充分条件；
解 (2) 条件P: a=0，q: 那么ab=0.因为当a=0时，一定有ab=0，所以此命题是真命题，p是q的充分条件；
问题：如果“灯B亮”，那么是否一定需要“开关A闭合”呢？
将命题“如果p，那么q”中的条件p和结论q互换，变成“如果q，那么p”，称这个命题为原命题的逆命题.
命题“如果开关A闭合，那么灯B亮”的逆命题为“如果灯B亮，那么开关A闭合”.
一般地，若命题“如果p，那么q”的逆命题“如果q，那么p”是真命题，则称p是q的必要条件，记作p⇐q.
若命题“如果p，那么q”的逆命题“如果q，那么p”是假命题，则称p不是q的必要条件，记作p⇍q.
命题“如果灯B亮，那么开关A闭合”是真命题,所以“开关A闭合”是“灯B亮”的必要条件，即如果“灯B亮”，一定需要“开关A闭合”.
解 （1）因为“如果x+y为偶数，那么x、y都是偶数”的逆命题“如果x、y都是偶数，那么x+y为偶数”是真命题，所以如果x+y为偶数是x、y都是偶数必要条件.
（3）因为“a=b，那么|a|=|b|”的逆命题“如果|a|=|b|，那么a=b” 是假命题，所以如果a=b不是|a|=|b|必要条件.
(1) 读书部分： 教材章节1.1； (2) 书面作业： P184习题1.1的1,2,3,4.