22.2.6 一元二次方程的根与系数的关系 华师大版数学九年级上册课件

这是一份22.2.6 一元二次方程的根与系数的关系 华师大版数学九年级上册课件，共19页。

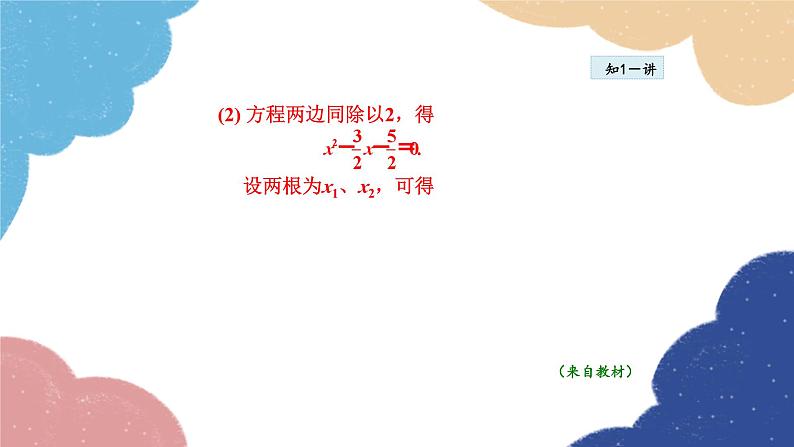
第6课时 一元二次方程的根与系数的关系22.2 一元二次方程的解法第二十二章 一元二次方程1课堂讲解一元二次方程根与系数的关系 一元二次方程根与系数的关系的应用2课时流程逐点导讲练课堂小结作业提升求出一元二次方程x2＋3x－4＝0的两根x1和x2，计算x1＋x2和x1·x2的值．它们与方程的系数有什么关系？试一试方程x2＋3x－4＝0的两根为x1＝1，x2＝－4，于是x1＋x2＝－3，x1·x2＝－4.我们发现：这个方程的二次项系数为1，它的两根之和－3等于一次项系数3的相反数，两根之积等于常数项－4.换几个一元二次方程再试试，结果怎样？ 对于任何一个二次项系数为1的一元二次方程，是否都有这样的结果呢？（来自教材）1知识点一元二次方程根与系数的关系知1－导 探究：我们来考察方程 x2＋px＋q＝0(p2－4q≥0)．由一 元二次方程的求根公式，得到方程的两根分别为1. 二次项系数为1的一元二次方程根与系数的关系： 设一元二次方程x2＋px＋q＝0的两根为x1、x2， 那么 x1＋x2＝－p， x1·x2＝q.知1－讲【例1】 不解方程，求出方程的两根之和与两根之积：(1)x2＋3x－5＝0；(2)2x2－3x－5＝0.解： (1) 设两根为x1、x2，由上述二次 项系数为1的一元二次方程根与 系数的关系，可得 x1＋x2＝－3，x1·x2＝－5.知1－讲 (2) 方程两边同除以2，得 设两根为x1、x2，可得 （来自教材）知1－讲（来自教材） 2. 试探索一元二次方程ax2＋bx＋c＝0 ( a≠0，b2－4ac≥0) 的根与系数的关系．解：方程两边同除以a，得 由二次项系数为1的一元二次方程根与系数的关系， 可得 这就是一般情形下一元二次方程的根与系数的关 系，前面概括的结论是它的特征(二次项系数为1)． 利用这个结论，我们可以直接写出例8中题(2)的答案：知1－讲（来自教材） 3. 一元二次方程根与系数的关系： 一元二次方程ax2＋bx＋c＝0 ( a≠0)，当b2－4ac≥0时， 方程有实数根，设这两个实数根分别为x1、x2，这 两个根与系数的关系是要点精析：(1) 一元二次方程的根与系数的关系成立的前 提条件是二次项系数不为0和方程有实数根． (2) 根与系数的关系刻画了一元二次方程的两根和、 两根积与系数a、b、c之间的关系．【例2】 不解方程，求下列方程的两根x1、x2的和与积. (1) x2－5x＋2＝0；(2) 4x2－2x－7＝0； (3) 3x2＋10＝2x2＋8x.知1－讲解：（来自教材）导引：根与系数的关系是建立在方程有根的前提条件下的； 系数是方程化为一般形式后的系数．一元二次方程x2＋4x－3＝0的两根为x1，x2，则x1·x2的值是(　　)A．4　 B．－4　 C．3　　D．－32 设x1，x2是方程x2＋5x－3＝0的两个根，则 的值是(　　)A．19 B．25 C．31 D．30知1－练2知识点一元二次方程根与系数的关系的应用知2－讲1. 利用根与系数的关系求值：（来自教材）【例3】已知关于x的方程 x2－6x＋p2－2p＋5＝0的一个 根是2，求方程的另一个根和p的值．导引：已知二次项系数与一次项系数，利用两根之和 可求出另一根，再运用两根之积求出常数项中 p的值．知2－讲解： 设方程的两根为x1和x2， ∵x1＋x2＝6，x1＝2，∴x2＝4. 又∵x1x2＝ ＝p2－2p＋5＝2×4＝8， ∴p2－2p－3＝0，解得p＝3或p＝－1.知2－讲 已知方程的一根求另一根，可以直接将一根代入方程中求出待定字母的值，然后再解方程求另一根．也可以直接利用根与系数的关系求另一根及待定字母的值．知2－讲（来自教材）2. 已知方程两根的关系求方程中待定的字母系数的值：【例4】 〈山东德州改编〉方程x2＋2kx＋k2－2k＋1＝0 的两个实数根x1、x2满足x12＋x22 ＝ 4 ，求k的值．导引：由x12＋x22＝x12＋2x1·x2＋x22－2x1·x2＝(x1＋x2)2 －2x1·x2＝4，然后根据根与系数的关系即可得 到一个关于k的方程，从而求得k的值．知2－讲解： x12＋x22＝4， 即x12＋x22＝x12＋2x1·x2＋x22－2x1·x2 ＝(x1＋x2)2－2x1·x2＝4 将x1＋x2＝－2k，x1·x2＝k2－2k＋1， 代入上式有4k2－2(k2－2k＋1)＝4， 解得k＝1或k＝－3. 当k＝－3时，(2k)2－4(k2－2k＋1)＝－28＜0， 不符合题意舍去，∴k＝1.知2－讲 已知方程两根的关系求待定字母系数的值： 先根据根与系数的关系用待定的字母表示两根之和与两根之积，然后将已知两根的关系进行变形，然后将两根的和与积整体代入，列出以待定字母为未知数的方程，求出待定字母的值，求出待定字母的值必须满足根的判别式大于或等于0.若关于x的方程x2＋3x＋a＝0有一 个根为－1，则另一个根为(　　) A．－2 B．2 C．4 D．－3若关于x的一元二次方程x2＋kx＋4k2－3＝0的 两个实数根分别是x1，x2，且满足x1＋x2＝x1x2， 则k的值为(　　) A．－1或　　B．－1　　C.　 　D．不存在知2－练1一元二次方程根与系数的关系：一元二次方程ax2＋bx＋c＝0(a≠0)，当b2－4ac≥0时，方程有实数根，设这两个实数根分别为x1、x2，这两个根与系数的关系是x1＋x2＝ x1·x2＝一元二次方程根与系数的关系的几种常用变形：(1)x12＋x22＝(x1＋x2)2－2x1x2；　　　　　　　　　(2)(x1－x2)2＝(x1＋x2)2－4x1x2；(3)(x1＋1)(x2＋1)＝x1x2＋(x1＋x2)＋1；　 2