2021-2022学年北京市西城区月坛中学九年级（上）期中数学试卷【含解析】

这是一份2021-2022学年北京市西城区月坛中学九年级（上）期中数学试卷【含解析】，共25页。试卷主要包含了2+2的最大值是 　 　等内容，欢迎下载使用。

1．（3分）剪纸是我们国家特别悠久的民间艺术形式之一，它是人们用祥和的图案企望吉祥、幸福的一种寄托．下列剪纸图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
2．（3分）抛物线y＝（x﹣1）2+2的对称轴为（ ）
A．直线x＝1B．直线x＝﹣1C．直线x＝2D．直线x＝﹣2
3．（3分）如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则∠B的大小为（ ）
A．30°B．40°C．50°D．60°
4．（3分）如图，点A、B、C是⊙O上的点，∠AOB＝70°，则∠ACB的度数是（ ）
A．30°B．35°C．45°D．70°
5．（3分）如图，已知AB是⊙O的直径，＝＝．∠BOC＝40°，那么∠AOE＝（ ）
A．40°B．60°C．80°D．120°
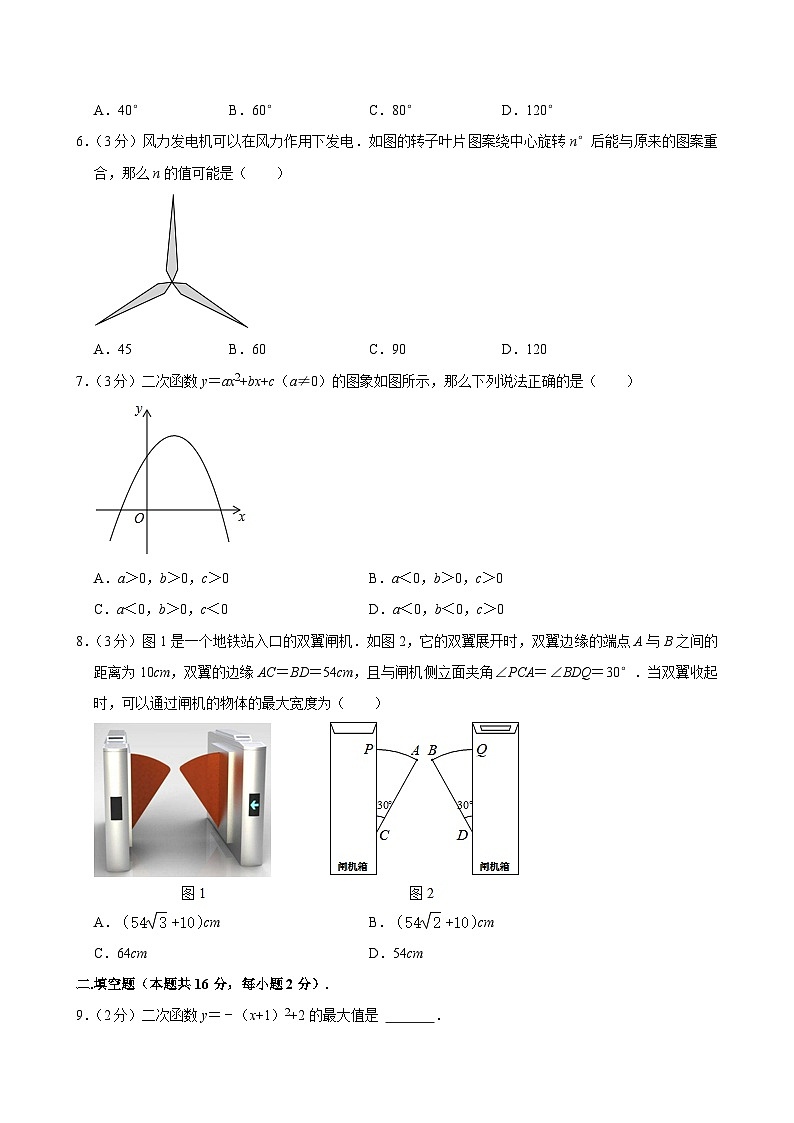
6．（3分）风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n°后能与原来的图案重合，那么n的值可能是（ ）
A．45B．60C．90D．120
7．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，那么下列说法正确的是（ ）
A．a＞0，b＞0，c＞0B．a＜0，b＞0，c＞0
C．a＜0，b＞0，c＜0D．a＜0，b＜0，c＞0
8．（3分）图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为（ ）
A．cmB．cm
C．64cmD．54cm
二.填空题（本题共16分，每小题2分）.
9．（2分）二次函数y＝﹣（x+1）2+2的最大值是 ．
10．（2分）点A（2，1）关于原点对称的点B的坐标为 ．
11．（2分）写出一个二次函数，其图象满足：（1）开口向下；（2）与y轴交于点（0，3），这个二次函数的解析式可以是 ．
12．（2分）关于x的方程x2+2x+k＝0有两个相等的实数根，则k的值为 ．
13．（2分）点A（﹣3，y1），B（2，y2）在抛物线y＝x2﹣5x上，则y1 y2．（填“＞”，“＜”或“＝”）
14．（2分）将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA＝2，将三角板绕原点O顺时针旋转90°，则点A的对应点A′的坐标为 ．
15．（2分）如图，直线y1＝kx+n（k≠0）与抛物线y2＝ax2+bx+c（a≠0）分别交于A（﹣1，0），B（2，﹣3）两点，那么当y1＞y2时，x的取值范围是 ．
16．（2分）如图，舞台地面上有一段以点O为圆心的，某同学要站在的中点C的位置上．于是他想：只要从点O出发，沿着与弦AB垂直的方向走到上，就能找到的中点C，老师肯定了他的想法．这位同学确定点C所用方法的依据是 ．
三.解答题（本题共60分）.
17．解方程：
（1）x2﹣4x+3＝0．
（2）2x2﹣5x+1＝0．
18．如图，将其补全，使其成为中心对称图形．
19．如图，方格中每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图．
（1）画出将△ABC向右平移2个单位得到的△A1B1C1；
（2）画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2．
20．已知一元二次方程x2﹣（2m﹣1）x+m2﹣m＝0．
（1）求证：此方程有两个不相等的实数根；
（2）若抛物线y＝x2﹣（2m﹣1）x+m2﹣m经过原点，求m的值．
21．已知二次函数的解析式是y＝ax2+bx经过点（2，0）和（1，﹣1），求a、b值，开口方向及二次函数解析式．
22．已知二次函数的解析式是y＝x2﹣2x﹣3．
（1）把其化成y＝a（x﹣h）2+k的形式 ；此函数图象与x轴的交点坐标是 ．
（2）在坐标系中利用描点法画出此抛物线；
（3）当x 时，y随x的增大而增大．
23．已知，如图，A、B、C、D是⊙O上的点，∠AOB＝∠COD．求证：AC＝BD．
24．如图，⊙O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，求CD的长．
25．如图1是博物馆展出的古代车轮实物，《周礼•考工记》记载：“…故兵车之轮六尺有六寸，田车之轮六尺有三寸…”据此，我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．
如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为r cm．
作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理依据是： ．
经测量：AB＝90cm，CD＝15cm，则AD＝ cm；
用含r的代数式表示OD，OD＝ cm．
在Rt△OAD中，由勾股定理可列出关于r的方程：
r2＝ ，
解得r＝75．
通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．
26．跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分．一名运动员起跳后，他的飞行路线如图所示，当他的水平距离为15m时，达到飞行的最高点C处，此时的竖直高度为45m，他落地时的水平距离（即OA的长）为60m，求这名运动员起跳时的竖直高度（即OB的长）．
27．关于x的一元二次方程ax2+bx+c＝0（a＞0）有两个不相等且非零的实数根，探究a，b，c满足的条件．
小华根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小华的探究过程，第一步，设一元二次方程ax2+bx+c＝0（a＞0）对应的二次函数为y＝ax2+bx+c（a＞0）；
第二步：借助二次函数图象．可以得到相应的一元二次方程中a，b，c满足的条件，列表如下：
（1）请帮助小华将上述表格补充完整；
（2）参考小华的做法，解决问题：
若关于x的一元二次方程x2﹣（m+5）x﹣2m＝0有一个负实根和一个正实根，且负实根大于﹣1，求实数m的取值范围．
28．如图，在△ABC中，AC＝BC，∠ACB＝90°，D是线段AC延长线上一点，连接BD，过点A作AE⊥BD于 E．
（1）求证：∠CAE＝∠CBD．
（2）将射线AE绕点A顺时针旋转45°后，所得的射线与线段BD的延长线交于点F，连接CE．
①依题意补全图形；
②用等式表示线段EF，CE，BE之间的数量关系，并证明．
2021-2022学年北京市西城区月坛中学九年级（上）期中数学试卷
参考答案与试题解析
一.选择题（本题共24分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的．
1．（3分）剪纸是我们国家特别悠久的民间艺术形式之一，它是人们用祥和的图案企望吉祥、幸福的一种寄托．下列剪纸图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．
C．D．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：A、是轴对称图形，不是中心对称图形，故此选项不合题意；
B、不是轴对称图形，是中心对称图形，故此选项不合题意；
C、既是轴对称图形又是中心对称图形，故此选项符合题意；
D、不是轴对称图形，也不是中心对称图形，故此选项不合题意；
故选：C．
【点评】本题考查了中心对称及轴对称的知识，解题时掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
2．（3分）抛物线y＝（x﹣1）2+2的对称轴为（ ）
A．直线x＝1B．直线x＝﹣1C．直线x＝2D．直线x＝﹣2
【分析】由抛物线解析式可求得答案．
【解答】解：
∵y＝（x﹣1）2+2，
∴对称轴为直线x＝1，
故选：A．
【点评】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y＝a（x﹣h）2+k中，对称轴为x＝h，顶点坐标为（h，k）．
3．（3分）如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则∠B的大小为（ ）
A．30°B．40°C．50°D．60°
【分析】根据旋转的性质可得出AB＝AD、∠BAD＝100°，再根据等腰三角形的性质可求出∠B的度数，此题得解．
【解答】解：根据旋转的性质，可得：AB＝AD，∠BAD＝100°，
∴∠B＝∠ADB＝×（180°﹣100°）＝40°．
故选：B．
【点评】本题考查了旋转的性质以及等腰三角形的性质，根据旋转的性质结合等腰三角形的性质求出∠B的度数是解题的关键．
4．（3分）如图，点A、B、C是⊙O上的点，∠AOB＝70°，则∠ACB的度数是（ ）
A．30°B．35°C．45°D．70°
【分析】根据圆周角定理得到∠ACB＝∠AOB，即可计算出∠ACB．
【解答】解：∵∠AOB＝70°，
∴∠ACB＝∠AOB＝35°．
故选：B．
【点评】本题考查了圆周角定理：一条弧所对的圆周角是它所对的圆心角的一半．
5．（3分）如图，已知AB是⊙O的直径，＝＝．∠BOC＝40°，那么∠AOE＝（ ）
A．40°B．60°C．80°D．120°
【分析】根据圆心角与弦的关系可求得∠BOE的度数，从而即可求解．
【解答】解：∵＝＝，∠BOC＝40°
∴∠BOE＝3∠BOC＝120°
∴∠AOE＝180﹣∠BOE＝60°
故选：B．
【点评】本题主要考查圆心角、弧、弦的关系的掌握情况．
6．（3分）风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转n°后能与原来的图案重合，那么n的值可能是（ ）
A．45B．60C．90D．120
【分析】该图形被平分成三部分，因而每部分被分成的圆心角是120°，并且圆具有旋转不变性，因而旋转120度的整数倍，就可以与自身重合．
【解答】解：该图形被平分成三部分，旋转120°的整数倍，就可以与自身重合，
故n的最小值为120．
故选：D．
【点评】本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．
7．（3分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，那么下列说法正确的是（ ）
A．a＞0，b＞0，c＞0B．a＜0，b＞0，c＞0
C．a＜0，b＞0，c＜0D．a＜0，b＜0，c＞0
【分析】利用抛物线开口方向确定a的符号，利用对称轴方程可确定b的符号，利用抛物线与y轴的交点位置可确定c的符号．
【解答】解：∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴在y轴的右侧，
∴x＝﹣＞0，
∴b＞0，
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
故选：B．
【点评】本题考查了二次函数图象与系数的关系：对于二次函数y＝ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：Δ＝b2﹣4ac＞0时，抛物线与x轴有2个交点；Δ＝b2﹣4ac＝0时，抛物线与x轴有1个交点；Δ＝b2﹣4ac＜0时，抛物线与x轴没有交点．
8．（3分）图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为（ ）
A．cmB．cm
C．64cmD．54cm
【分析】过A作AE⊥CP于E，过B作BF⊥DQ于F，则可得AE和BF的长，依据端点A与B之间的距离为10cm，即可得到可以通过闸机的物体的最大宽度．
【解答】解：如图所示，过A作AE⊥CP于E，过B作BF⊥DQ于F，则
Rt△ACE中，AE＝AC＝×54＝27（cm），
同理可得，BF＝27cm，
又∵点A与B之间的距离为10cm，
∴通过闸机的物体的最大宽度为27+10+27＝64（cm），
故选：C．
【点评】本题主要考查了特殊角的三角函数值，特殊角的三角函数值应用广泛，一是它可以当作数进行运算，二是具有三角函数的特点，在解直角三角形中应用较多．
二.填空题（本题共16分，每小题2分）.
9．（2分）二次函数y＝﹣（x+1）2+2的最大值是 2 ．
【分析】根据二次函数顶点特点可知，当x＝﹣1时，函数有最大值．
【解答】解：∵二次函数y＝﹣（x+1）2+2，
∴抛物线开口向下，顶点为（﹣1，2），
∴当x＝﹣1时，函数有最大值2，
故答案为：2．
【点评】本题考查二次函数的最值，熟练掌握由二次函数的顶点式求最值的方法是解题的关键．
10．（2分）点A（2，1）关于原点对称的点B的坐标为 （﹣2，﹣1） ．
【分析】根据点A和点B关于原点对称可知，B点的坐标与A点的坐标互为相反数．
【解答】解：∵点A（﹣2，﹣1）与B关于原点对称，
∴点A和点B的横、纵坐标分别互为相反数，
∴B点坐标为（﹣2，﹣1）．
故答案为（﹣2，﹣1）．
【点评】本题考查了平面直角坐标系中任意一点P（x，y）关于原点的对称点是（﹣x，﹣y），即关于原点的对称点，横纵坐标都变成相反数．
11．（2分）写出一个二次函数，其图象满足：（1）开口向下；（2）与y轴交于点（0，3），这个二次函数的解析式可以是 y＝﹣x2+3（答案不唯一） ．
【分析】根据二次函数的性质可得出a＜0，利用二次函数图象上点的坐标特征可得出c＝3，取a＝﹣1，b＝0即可得出结论．
【解答】解：设二次函数的解析式为y＝ax2+bx+c．
∵抛物线开口向下，
∴a＜0．
∵抛物线与y轴的交点坐标为（0，3），
∴c＝3．
取a＝﹣1，b＝0时，二次函数的解析式为y＝﹣x2+3．
故答案为：y＝﹣x2+3（答案不唯一）．
【点评】本题考查了二次函数的性质以及二次函数图象上点的坐标特征，利用二次函数的性质及二次函数图象上点的坐标特征，找出a＜0，c＝3是解题的关键．
12．（2分）关于x的方程x2+2x+k＝0有两个相等的实数根，则k的值为 1 ．
【分析】根据根的判别式Δ＝0，即可得出关于k的一元一次方程，解之即可得出k值．
【解答】解：∵关于x的方程x2+2x+k＝0有两个相等的实数根，
∴Δ＝22﹣4×1×k＝0，
解得：k＝1．
故答案为：1．
【点评】本题考查了根的判别式，牢记“当Δ＝0时，方程有两个相等的实数根”是解题的关键．
13．（2分）点A（﹣3，y1），B（2，y2）在抛物线y＝x2﹣5x上，则y1 ＞ y2．（填“＞”，“＜”或“＝”）
【分析】分别计算自变量为﹣3、2时的函数值，然后比较函数值的大小即可．
【解答】解：当x＝﹣3时，y1＝x2﹣5x＝24；
当x＝2时，y2＝x2﹣5x＝﹣6；
∵24＞﹣6，
∴y1＞y2．
故答案为：＞．
【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．
14．（2分）将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA＝2，将三角板绕原点O顺时针旋转90°，则点A的对应点A′的坐标为 （1，﹣） ．
【分析】如图，过点A′作A′H⊥OB于点H．解直角三角形求出OH，A′H可得结论．
【解答】解：如图，过点A′作A′H⊥OB于点H．
在Rt△OA′H中，∠OHA′＝90°，OA＝2，∠A′OH＝60°，
∴OH＝OA′•cs60°＝1，A′H＝，
∴A′（1，﹣），
故答案为：（1，﹣）．
【点评】本题考查旋转变换，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．
15．（2分）如图，直线y1＝kx+n（k≠0）与抛物线y2＝ax2+bx+c（a≠0）分别交于A（﹣1，0），B（2，﹣3）两点，那么当y1＞y2时，x的取值范围是 ﹣1＜x＜2 ．
【分析】根据图象得出取值范围即可．
【解答】解：因为直线y1＝kx+n（k≠0）与抛物线y2＝ax2+bx+c（a≠0）分别交于A（﹣1，0），B（2，﹣3）两点，
所以当y1＞y2时，﹣1＜x＜2，
故答案为：﹣1＜x＜2
【点评】此题考查二次函数与不等式，关键是根据图象得出取值范围．
16．（2分）如图，舞台地面上有一段以点O为圆心的，某同学要站在的中点C的位置上．于是他想：只要从点O出发，沿着与弦AB垂直的方向走到上，就能找到的中点C，老师肯定了他的想法．这位同学确定点C所用方法的依据是 垂径定理 ．
【分析】由垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．即可得出结论．
【解答】解：这位同学确定点C所用方法的依据是：垂径定理，
即垂直于弦的直径平分弦，并且平分弦所对的两条弧，
故答案为：垂径定理．
【点评】本题考查了垂径定理，熟练掌握垂径定理是解题的关键．
三.解答题（本题共60分）.
17．解方程：
（1）x2﹣4x+3＝0．
（2）2x2﹣5x+1＝0．
【分析】（1）利用十字相乘法将方程的左边因式分解后求解可得；
（2）利用公式法求解即可．
【解答】解：（1）∵x2﹣4x+3＝0，
∴（x﹣1）（x﹣3）＝0，
∴x﹣1＝0或x﹣3＝0，
则x1＝1，x2＝3；
（2）∵a＝2，b＝﹣5，c＝1，
∴Δ＝（﹣5）2﹣4×2×1＝17＞0，
∴x＝＝，
则x1＝，x2＝．
【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
18．如图，将其补全，使其成为中心对称图形．
【分析】根据中心对称图形的性质把原图补充完整即可．
【解答】解：如图所示：就是中心对称图形．
【点评】本题考查的是利用旋转设计图案，熟知中心对称图形旋转180°后所得图形与原图形完全重合是解答此题的关键．
19．如图，方格中每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图．
（1）画出将△ABC向右平移2个单位得到的△A1B1C1；
（2）画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2．
【分析】（1）根据平移的性质，画出对应点的位置即可；
（2）根据旋转的性质，画出对应点的位置即可．
【解答】解：（1）如图所示，即为所求，
（2）如图所示，即为所求，
【点评】本题主要考查了作图﹣平移变换，旋转变换，熟练掌握平移和旋转的性质是解题的关键，属于常考题．
20．已知一元二次方程x2﹣（2m﹣1）x+m2﹣m＝0．
（1）求证：此方程有两个不相等的实数根；
（2）若抛物线y＝x2﹣（2m﹣1）x+m2﹣m经过原点，求m的值．
【分析】（1）根据二次函数的根的判别式Δ＝b2﹣4ac的符号来判断方程的根的情况；
（2）抛物线过原点，则m2﹣m＝0，即可求解．
【解答】解：（1）由题意有Δ＝[﹣（2m﹣1）]2﹣4（m2﹣m）＝1＞0．
∴不论m取何值时，方程总有两个不相等的实数根；
（2）抛物线过原点，则m2﹣m＝0，解得m＝0或1．
【点评】本题考查了抛物线和x轴的交点、根与系数的关系等，熟练掌握根的判别式是解题的关键．
21．已知二次函数的解析式是y＝ax2+bx经过点（2，0）和（1，﹣1），求a、b值，开口方向及二次函数解析式．
【分析】将点（2，0）、（1，﹣1）代入二次函数的解析式，利用待定系数法法求该二次函数的解析式即可．
【解答】解：根据题意，得，
解得，；
∴该二次函数的解析式为：y＝x2﹣2x，开口向上．
【点评】本题主要考查了待定系数法求二次函数的解析式．解题时，借用了二次函数图象上点的坐标特征：经过图象上的点一定在函数图象上，且图象上的每一个点均满足该函数的解析式．
22．已知二次函数的解析式是y＝x2﹣2x﹣3．
（1）把其化成y＝a（x﹣h）2+k的形式 y＝（x﹣1）2﹣4 ；此函数图象与x轴的交点坐标是 （﹣1，0），（3，0） ．
（2）在坐标系中利用描点法画出此抛物线；
（3）当x ＞1 时，y随x的增大而增大．
【分析】（1）用配方法把二次函数解析式的一般式化为顶点式即可；令y＝0，解关于x的一元二次方程即可求出抛物线与x轴的交点；
（2）用五点法做函数图象即可；
（3）结合函数图象直接得出结论．
【解答】解：（1）y＝x2﹣2x﹣3
＝x2﹣2x+1﹣1﹣3
＝（x﹣1）2﹣4，
令y＝0，则x2﹣2x﹣3＝0，
解得：x1＝﹣1，x2＝3，
∴函数图象与x轴的交点坐标是（﹣1，0）和（3，0），
故答案为：y＝（x﹣1）2﹣4，（﹣1，0），（3，0）；
（2）列表：
描点、连线画出函数图象
（3）由图象可知，当x＞1时，y随x的增大而增大；
故答案为：＞1．
【点评】本题考查二次函数与x轴的交点，二次函数的性质，五点法作二次函数的图象，数形结合等知识，关键是对二次函数性质的综合运用．
23．已知，如图，A、B、C、D是⊙O上的点，∠AOB＝∠COD．求证：AC＝BD．
【分析】根据圆心角、弧、弦之间的关系定理得到∠AOC＝∠BOD，进而证明结论．
【解答】证明：∵∠AOB＝∠COD，
∴∠AOB+∠BOC＝∠COD+∠BOC，
∴∠AOC＝∠BOD，
∴AC＝BD．
【点评】本题考查的是圆心角、弧、弦之间的关系定理，在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
24．如图，⊙O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，求CD的长．
【分析】证明△EOC是等腰直角三角形，求出EC，再利用垂径定理解决问题即可．
【解答】解：∵∠A＝22.5°，
∴∠BOC＝2∠A＝45°，
∵圆O的直径AB垂直于弦，
∴CE＝ED＝，
∴Rt△CEO中，OC＝4，
∴CE＝EO＝OC＝2，
∴CD＝4．
【点评】本题考查圆周角定理，垂径定理，等腰直角三角形的判定和性质等知识，解题的关键是证明△OCE是等腰直角三角形．
25．如图1是博物馆展出的古代车轮实物，《周礼•考工记》记载：“…故兵车之轮六尺有六寸，田车之轮六尺有三寸…”据此，我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．
如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为r cm．
作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理依据是： 垂直弦的直径平分弦 ．
经测量：AB＝90cm，CD＝15cm，则AD＝ 45 cm；
用含r的代数式表示OD，OD＝ （r﹣15） cm．
在Rt△OAD中，由勾股定理可列出关于r的方程：
r2＝ 452+（r﹣15）2 ，
解得r＝75．
通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．
【分析】根据垂径定理，利用勾股定理构建方程求解即可．
【解答】解：如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为r cm．
作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理依据是：垂直弦的直径平分弦．
经测量：AB＝90cm，CD＝15cm，则AD＝45cm；
用含r的代数式表示OD，OD＝（r﹣15）cm．
在Rt△OAD中，由勾股定理可列出关于r的方程：
r2＝452+（r﹣15）2，
解得r＝75．
通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．
故答案为：垂直弦的直径平分弦，45，（r﹣15），452+（r﹣15）2．
【点评】本题考查垂径定理，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．
26．跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分．一名运动员起跳后，他的飞行路线如图所示，当他的水平距离为15m时，达到飞行的最高点C处，此时的竖直高度为45m，他落地时的水平距离（即OA的长）为60m，求这名运动员起跳时的竖直高度（即OB的长）．
【分析】利用待定系数法确定抛物线的解析式后求得与y轴的交点即可确定本题的答案．
【解答】解：设抛物线的解析式为y＝a（x﹣h）2+k，
根据题意得：抛物线的顶点坐标为（15，45），
∴y＝a（x﹣15）2+45，
∵与x轴交于点A（60，0），
∴0＝a（60﹣15）2+45，
解得：a＝﹣，
∴解析式为y＝﹣（x﹣15）2+45，
令x＝0得：y＝﹣（0﹣15）2+45＝40，
∴点B的坐标为（0，40），
∴这名运动员起跳时的竖直高度为40米．
【点评】此题考查了二次函数的应用，解题的关键是将实际问题转化为数学问题，难度中等．
27．关于x的一元二次方程ax2+bx+c＝0（a＞0）有两个不相等且非零的实数根，探究a，b，c满足的条件．
小华根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小华的探究过程，第一步，设一元二次方程ax2+bx+c＝0（a＞0）对应的二次函数为y＝ax2+bx+c（a＞0）；
第二步：借助二次函数图象．可以得到相应的一元二次方程中a，b，c满足的条件，列表如下：
（1）请帮助小华将上述表格补充完整；
（2）参考小华的做法，解决问题：
若关于x的一元二次方程x2﹣（m+5）x﹣2m＝0有一个负实根和一个正实根，且负实根大于﹣1，求实数m的取值范围．
【分析】（1）有题意即可求解；
（2）由讨论中的第二种情况，可得：c＞0，且x＝﹣1时，y＞0，即可求解．
【解答】解：（1）有题意得：①答案为：方程有两个异号的实数根；
②答案如图所示；
③答案为：a＞0，Δ＞0，﹣＞0，c＞0；
（2）由讨论中的第二种情况，可得：c＜0，且x＝﹣1时，y＞0，
即﹣2m＜0且y＝1+（m+5）﹣2m＞0，
解得：0＜m＜6．
【点评】本题考查的是二次函数综合运用，主要考查的是函数的基本性质，关键在于理解题意，按照题设的思路和逻辑求解即可．
28．如图，在△ABC中，AC＝BC，∠ACB＝90°，D是线段AC延长线上一点，连接BD，过点A作AE⊥BD于 E．
（1）求证：∠CAE＝∠CBD．
（2）将射线AE绕点A顺时针旋转45°后，所得的射线与线段BD的延长线交于点F，连接CE．
①依题意补全图形；
②用等式表示线段EF，CE，BE之间的数量关系，并证明．
【分析】（1）利用同角的余角即可得出结论；
（2）①根据题意补全图形；
②过点C作CG⊥CE角AE于G，进而判断出∠CAE＝∠CBD，即可判断出△ACG≌△BCE（ASA），得出AG＝BE，CG＝CE，
进而判断出EG＝CE，得出AE＝BE+CE，再判断出EF＝AE，即可得出结论．
【解答】解：（1）∵∠ACB＝90°，
∴∠BCD＝90°，
∴∠CBD+∠BDC＝90°，
∵AE⊥BD，
∴∠AED＝90°，
∴∠CAE+∠BDC＝90°，
∴∠CAE＝∠CBD；
（2）①由题意补全图形如图所示：
②过点C作CG⊥CE交AE于G，
∴∠BCG+∠BCE＝90°，
∵∠ACB＝90°，
∴∠ACG+∠BCG＝90°，
∴∠ACG＝∠BCE，
由（1）知，∠CAE＝∠CBD，
在△ACG和△BCE中，，
∴△ACG≌△BCE（ASA），
∴AG＝BE，CG＝CE，
在Rt△ECG中，CG＝CE，
∴EG＝CE，
∴AE＝AG+EG＝BE+CE，
由旋转知，∠EAF＝45°，
∵∠AEF＝90°，
∴∠F＝90°﹣∠EAF＝45°＝∠EAF，
∴EF＝AE，
∴EF＝BE+CE．
【点评】此题是几何变换综合题，主要考查了同角的余角相等，等腰直角三角形的判定和性质，全等三角形的判定和性质，勾股定理，构造出全等三角形是解本题的关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/7/21 21:50:21；用户：菁优校本题库；邮箱：2471@xyh.cm；学号：56380052x
…
…
y
…
…
方程两根的情况
对应的二次函数的大致图象
a，b，c满足的条件
方程有两个不相等的负实根

①

方程有两个不相等的正实根
②
③
x
…
…
y
…
…
x
…
﹣1
0
1
2
3
…
y
…
0
﹣3
﹣4
﹣3
0
…
方程两根的情况
对应的二次函数的大致图象
a，b，c满足的条件
方程有两个不相等的负实根

① 方程有两个异号的实数根

方程有两个不相等的正实根
②
③