
2021-2022学年北京市房山区九年级(上)期中数学试卷【含解析】
展开1.(2分)二次函数y=(x﹣3)2+1的图象的顶点坐标是( )
A.(3,﹣1)B.(﹣3,1)C.(﹣3,﹣1)D.(3,1)
2.(2分)已知,则的值为( )
A.B.C.D.2
3.(2分)已知两条直线被三条平行线所截,截得线段的长度如图所示,则x的值为( )
A.3B.4C.5D.6
4.(2分)如果两个相似三角形的面积之比为9:4,那么这两个三角形的周长之比为( )
A.81:16B.27:12C.9:4D.3:2
5.(2分)如图是测量河宽的示意图,测得BD=150m,DC=75m,EC=60m,则河宽AB的长为( )
A.60mB.80mC.100mD.120m
6.(2分)已知二次函数y=x2﹣1图象上三点:(﹣1,y1),(2,y2),(3,y3),比较y1,y2,y3的大小( )
A.y1<y3<y2B.y1<y2<y3C.y2<y1<y3D.y3<y2<y1
7.(2分)已知二次函数y=(x﹣2)2﹣6,当﹣1≤x≤4时,y的最小值为( )
A.3B.0C.﹣2D.﹣6
8.(2分)如图,用绳子围成周长为10m的矩形,记矩形的一边长为xm,矩形的面积为Sm2.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A.S=x(5﹣x)(0<x<5)B.S=x(10﹣x)(0<x<5)
C.S=x(x﹣5)(0<x<5)D.S=x(x﹣10)(0<x<5)
二、填空题(本题共8道小题,每小题2分,共16分
9.(2分)二次函数y=﹣2x2+4x+1图象的开口方向是 .
10.(2分)若2m=3n,那么m:n= .
11.(2分)如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度为 m.
12.(2分)如图,在△ABC中,点P是AB边上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是 .
13.(2分)如图Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为 .
14.(2分)如果二次函数y=mx2﹣2mx﹣3m的图象与y轴的交点为(0,3),那么m= .
15.(2分)写出抛物线y=2(x﹣1)2上一对关于对称轴对称的点的坐标,这对点的坐标可以是 和 .
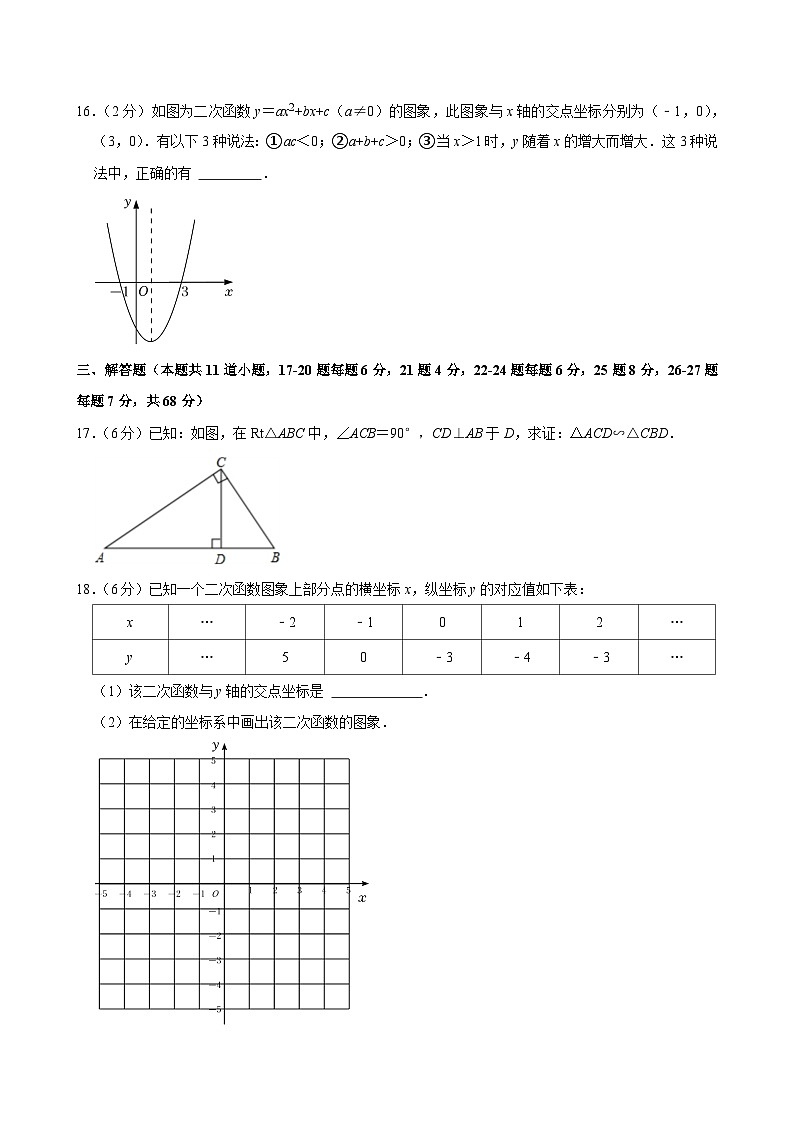
16.(2分)如图为二次函数y=ax2+bx+c(a≠0)的图象,此图象与x轴的交点坐标分别为(﹣1,0),(3,0).有以下3种说法:①ac<0;②a+b+c>0;③当x>1时,y随着x的增大而增大.这3种说法中,正确的有 .
三、解答题(本题共11道小题,17-20题每题6分,21题4分,22-24题每题6分,25题8分,26-27题每题7分,共68分)
17.(6分)已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,求证:△ACD∽△CBD.
18.(6分)已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
(1)该二次函数与y轴的交点坐标是 .
(2)在给定的坐标系中画出该二次函数的图象.
19.(6分)如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
20.(6分)已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)求该二次函数图象的顶点坐标.
21.(4分)如图是边长为1的正方形网格,△A1B1C1的顶点均为格点,在该网格中画出△A2B2C2(△A2B2C2的顶点均在格点上),使△A2B2C2∽△A1B1C1.
22.(6分)在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象过点A(1,0)和B(0,﹣3).
(1)求此二次函数的表达式;
(2)设此二次函数图象的顶点为C,写出一个过点C的二次函数的表达式.
23.(6分)如图,在△ABC中,D,E分别是边AB,AC上的点,连接DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)如果E是AC的中点,AD=8,AB=10,求AE的长.
24.(6分)在矩形ABCD中,AB=10,BC=12,点E为DC的中点,连接BE,过点A作AF⊥BE,垂足为点F.
(1)求证:△BEC∽△ABF;
(2)求AF的长.
25.(8分)已知二次函数y=x2﹣4x+3.
(1)该函数与x轴的交点坐标 ;
(2)在坐标系中,用描点法画出该二次函数的图象;
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
26.(7分)如图,AD是△ABC的中线,点O是AD上任一点,连接BO并延长,交AC于点E.
(1)如图1,当时,求的值;
(2)如图2,当时,求的值.
27.(7分)在平面直角坐标系xOy中,抛物线y=ax2+bx+3a过点A(﹣1,0).
(1)求抛物线的对称轴;
(2)直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C.如果该抛物线与线段BC有交点,结合函数的图象,求a的取值范围.
2021-2022学年北京市房山区九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共8道小题,每小题2分,共16分),下面各题均有四个选项,其中只有一个是符合题意的.
1.(2分)二次函数y=(x﹣3)2+1的图象的顶点坐标是( )
A.(3,﹣1)B.(﹣3,1)C.(﹣3,﹣1)D.(3,1)
【分析】根据抛物线y=a(x﹣h)2+k的顶点坐标是(h,k)直接写出即可.
【解答】解:抛物线y=(x﹣3)2+1的顶点坐标是(3,1).
故选:D.
【点评】此题主要考查了二次函数的性质,关键是熟记:抛物线y=a(x﹣h)2+k的顶点坐标是(h,k),对称轴是直线x=h.
2.(2分)已知,则的值为( )
A.B.C.D.2
【分析】先把化成+1,再把=代入计算即可得出答案.
【解答】解:∵=,
∴=+1=+1=.
故选:C.
【点评】此题考查了比例的性质,熟练掌握比例的基本性质是解题的关键.
3.(2分)已知两条直线被三条平行线所截,截得线段的长度如图所示,则x的值为( )
A.3B.4C.5D.6
【分析】由平行线分线段成比例定理得出比例式,即可得出结果.
【解答】解:∵两条直线被三条平行线所截,
∴,
解得:x=4,
故选:B.
【点评】本题考查了平行线分线段成比例定理;由平行线分线段成比例定理得出比例式是解决问题的关键.
4.(2分)如果两个相似三角形的面积之比为9:4,那么这两个三角形的周长之比为( )
A.81:16B.27:12C.9:4D.3:2
【分析】直接根据相似三角形的性质即可得出结论.
【解答】解:∵两个相似三角形的面积之比为9:4,
∴相似比是3:2,
∵相似三角形的周长比等于相似比,
∴这两个三角形的周长之比为:3:2,
故选:D.
【点评】本题考查的是相似三角形的性质,熟知相似三角形的面积的比等于相似比的平方是解答此题的关键.
5.(2分)如图是测量河宽的示意图,测得BD=150m,DC=75m,EC=60m,则河宽AB的长为( )
A.60mB.80mC.100mD.120m
【分析】先证明△ABD∽△ECD,然后利用相似比计算AB的长即可.
【解答】解:∵AB⊥BC,CE⊥BC,
∴AB∥CE,
∴△ABD∽△ECD,
∴=,即=,
∴AB=120(m).
∴河宽AB为120m.
故选:D.
【点评】本题考查了相似三角形的应用,正确得出相似三角形是解题关键.
6.(2分)已知二次函数y=x2﹣1图象上三点:(﹣1,y1),(2,y2),(3,y3),比较y1,y2,y3的大小( )
A.y1<y3<y2B.y1<y2<y3C.y2<y1<y3D.y3<y2<y1
【分析】将三个点的横坐标分别代入解析式,求出相应的函数值,再进行比较即可.
【解答】解:将点(﹣1,y1),(2,y2),(3,y3)分别代入y=x2﹣1得,
y1=1﹣1=0,
y2=4﹣1=3,
y3=9﹣1=8.
可见y1<y2<y3.
故选:B.
【点评】本题考查了二次函数图象上点的坐标特征,由于函数图象上的点符合函数解析式,将各点代入,求出函数值比较其大小是最简捷的方法.
7.(2分)已知二次函数y=(x﹣2)2﹣6,当﹣1≤x≤4时,y的最小值为( )
A.3B.0C.﹣2D.﹣6
【分析】根据题目中的函数解析式和二次函数的性质,可以得到当1≤x≤4时该函数的最小值.
【解答】解:∵二次函数y=(x﹣2)2﹣6,
∴该函数图象的开口向上,对称轴为直线x=2,当x=2时取得最小值﹣6,
∵﹣1≤x≤4,
∴当x=2取得最小值﹣6,
故选:D.
【点评】本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.
8.(2分)如图,用绳子围成周长为10m的矩形,记矩形的一边长为xm,矩形的面积为Sm2.当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数表达式为( )
A.S=x(5﹣x)(0<x<5)B.S=x(10﹣x)(0<x<5)
C.S=x(x﹣5)(0<x<5)D.S=x(x﹣10)(0<x<5)
【分析】由矩形周长可得x与y的关系,然后由S=xy求解.
【解答】解:由题意得2(x+y)=10,
即y=5﹣x,
∴S=xy=x(5﹣x),
故选:A.
【点评】本题考查二次函数的应用,解题关键是掌握求矩形周长与面积的方法.
二、填空题(本题共8道小题,每小题2分,共16分
9.(2分)二次函数y=﹣2x2+4x+1图象的开口方向是 下 .
【分析】根据二次函数y=﹣2x2+4x+1中a=﹣2<0,即可判定.
【解答】解:∵y=﹣2x2+4x+1中a=﹣2<0,
∴图象的开口向下,
故答案为:下.
【点评】本题考查了二次函数的性质,通过a的符号即可判断开口方向.
10.(2分)若2m=3n,那么m:n= 3:2 .
【分析】逆用比例的性质:内项之积等于外项之积即可求解.
【解答】解:∵2m=3n,
∴m:n=3:2.
故答案为:3:2.
【点评】考查了比例的性质:内项之积等于外项之积.若=,则ad=bc.
11.(2分)如图,为了测量某棵树的高度,小明用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m,与树相距15m,则树的高度为 7 m.
【分析】此题中,竹竿、树以及经过竹竿顶端和树顶端的太阳光构成了一组相似三角形,利用相似三角形的对应边成比例即可求得树的高度.
【解答】解:如图;
AD=6m,AB=21m,DE=2m;
由于DE∥BC,所以△ADE∽△ABC,得:
,即,
解得:BC=7m,
故答案为:7.
【点评】此题考查了相似三角形在测量高度时的应用;解题的关键是找出题中的相似三角形,并建立适当的数学模型来解决问题.
12.(2分)如图,在△ABC中,点P是AB边上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是 ∠B=∠ACP或∠ACB=∠APC或 .
【分析】欲使△ACP∽△ABC,通过观察发现两个三角形有一个公共角,即∠A,若夹此对应角的两边对应成比例或有一组角对应相等即可.
【解答】解:∵∠A=∠A
∴当∠B=∠ACP或∠ACB=∠APC或时,△ACP∽△ABC.
故答案为:∠B=∠ACP或∠ACB=∠APC或.
【点评】本题考查相似三角形的判定方法的理解及运用,识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边成比例、对应角相等.
13.(2分)如图Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为 4 .
【分析】先证明△ADE∽△ACB,得出对应边成比例,即可求出AD的长.
【解答】解:∵ED⊥AB,
∴∠ADE=90°=∠C,
∵∠A=∠A,
∴△ADE∽△ACB,
∴,
即,
解得:AD=4.
故答案为:4.
【点评】本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定方法,证明三角形相似得出比例式是解决问题的关键.
14.(2分)如果二次函数y=mx2﹣2mx﹣3m的图象与y轴的交点为(0,3),那么m= ﹣1 .
【分析】将点(0,3)代入函数解析式即可求得m的值.
【解答】解:∵二次函数y=mx2﹣2mx﹣3m的图象与y轴的交点为(0,3),
∴﹣3m=3,
∴m=﹣1,
故答案为:﹣1.
【点评】本题考查了二次函数图象上点的坐标特征和二次函数的性质,图象上点的坐标适合解析式是解题的关键.
15.(2分)写出抛物线y=2(x﹣1)2上一对关于对称轴对称的点的坐标,这对点的坐标可以是 (2,2) 和 (0,2) .
【分析】根据抛物线的对称轴是直线x=1作答.
【解答】解:∵抛物线y=2(x﹣1)2的对称轴是直线x=1,
∴这对对称点的坐标可以是(2,2),(0,2)(答案不唯一).
故答案为:(2,2),(0,2)(答案不唯一).
【点评】考查了二次函数图象上点的坐标特征,二次函数图象与几何变换.需要掌握抛物线的轴对称性.
16.(2分)如图为二次函数y=ax2+bx+c(a≠0)的图象,此图象与x轴的交点坐标分别为(﹣1,0),(3,0).有以下3种说法:①ac<0;②a+b+c>0;③当x>1时,y随着x的增大而增大.这3种说法中,正确的有 ①③ .
【分析】由抛物线的开口方向、与y轴的交点判定a、c的符号即可判断①将x=1代入函数关系式,结合图象即可判断②;利用对称轴和二次函数的图象的性质即可判断③.
【解答】解:①∵该抛物线的开口方向向上,
∴a>0;
又∵该抛物线与y轴交于负半轴,
∴c<0,
∴ac<0;
故本选项正确;
②∵根据抛物线的图象知,该抛物线的对称轴是直线x==1,
∴当x=1时,y<0,
即a+b+c<0;
故本选项错误;
③由②知,该抛物线的对称轴是直线x=1,
∴当x>1时,y随着x的增大而增大;
故本选项正确;
综上所述,以上说法正确的是①③;
故答案为:①③.
【点评】主要考查图象与二次函数系数之间的关系,抛物线与x轴的交点,二次函数的性质,重点是从图象中找出重要信息.
三、解答题(本题共11道小题,17-20题每题6分,21题4分,22-24题每题6分,25题8分,26-27题每题7分,共68分)
17.(6分)已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,求证:△ACD∽△CBD.
【分析】根据垂直的定义得到∠ADC=∠BDC=90°,根据余角的性质得到∠A=∠BCD,由相似三角形的判定定理即可得到结论.
【解答】证明:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
【点评】本题考查了相似三角形的判定,垂直的定义,余角的性质,熟练掌握相似三角形的判定定理是解题的关键.
18.(6分)已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
(1)该二次函数与y轴的交点坐标是 (0,﹣3) .
(2)在给定的坐标系中画出该二次函数的图象.
【分析】(1)由函数图象经过点(0,﹣3),即可求得该二次函数与y轴的交点坐标是(0,﹣3);
(2)利用描点发法画函数图象;
【解答】解:(1)∵抛物线经过点(0,﹣3),
∴该二次函数与y轴的交点坐标是(0,﹣3);
故答案为:(0,﹣3);
(2)描点、连线,画出函数图象如图:
【点评】本题考查了二次函数图象和性质,二次函数图象上点的坐标特征,正确分析表格数据是解题的关键.
19.(6分)如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
【分析】根据平行线的性质可知∠AED=∠C,∠A=∠FEC,根据相似三角形的判定定理可知△ADE∽△EFC.
【解答】证明:∵DE∥BC,
∴∠AED=∠C.
又∵EF∥AB,
∴∠A=∠FEC.
∴△ADE∽△EFC.
【点评】本题考查的是平行线的性质及相似三角形的判定定理.
20.(6分)已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)求该二次函数图象的顶点坐标.
【分析】(1)运用配方法把一般式化为顶点式;
(2)根据顶点式得出即可.
【解答】解:(1)y=x2﹣2x﹣3=(x﹣1)2﹣4;
(2)∵y=(x﹣1)2﹣4,
∴该二次函数图象的顶点坐标是(1,﹣4).
【点评】本题考查的是二次函数的三种形式、二次函数的性质,掌握配方法把一般式化为顶点式是解题的关键.
21.(4分)如图是边长为1的正方形网格,△A1B1C1的顶点均为格点,在该网格中画出△A2B2C2(△A2B2C2的顶点均在格点上),使△A2B2C2∽△A1B1C1.
【分析】将△A1B1C1的各边都缩小2倍,画出图形即可.
【解答】解:如图,△A2B2C2即为所求.
【点评】本题主要考查了相似三角形的性质,熟练掌握相似三角形的性质是解题的关键.
22.(6分)在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象过点A(1,0)和B(0,﹣3).
(1)求此二次函数的表达式;
(2)设此二次函数图象的顶点为C,写出一个过点C的二次函数的表达式.
【分析】(1)把A(1,0)和点B(0,1)代入y=x2+bx+c得到关于b、c的方程组,解方程组即可;
(2)根据题意,可以写出一个点C的二次函数的解析式,答案不唯一.
【解答】解:(1)把A(1,0)和点B(0,﹣3)代入y=﹣x2+bx+c得,
解得,
所以这个二次函数的解析式为y=x2+2x﹣3;
(2)∵y=x2+2x﹣3=(x+1)2﹣4,
∴C(﹣1,﹣4),
∵二次函数y=﹣4x2的图象过点(﹣1,﹣4),
∴过点C的一个二次函数的表达式为y=﹣4x2,答案不唯一.
【点评】本题考查了待定系数法求二次函数的解析式:设二次函数的解析式为y=ax2+bx+c(a≠0),然后把二次函数图象上的点的坐标代入得到关于a、b、c的方程组,解方程组求出a、b、c的值,从而确定二次函数的解析式.
23.(6分)如图,在△ABC中,D,E分别是边AB,AC上的点,连接DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)如果E是AC的中点,AD=8,AB=10,求AE的长.
【分析】(1)根据相似三角形的判定即可求出证.
(2)由于点E是AC的中点,设AE=x,根据相似三角形的性质可知=,从而列出方程解出x的值.
【解答】解:(1)∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB;
(2)由(1)可知:△ADE∽△ACB,
∴=,
∵点E是AC的中点,设AE=x,
∴AC=2AE=2x,
∵AD=8,AB=10,
∴=,
解得:x=2,
∴AE=2.
【点评】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.
24.(6分)在矩形ABCD中,AB=10,BC=12,点E为DC的中点,连接BE,过点A作AF⊥BE,垂足为点F.
(1)求证:△BEC∽△ABF;
(2)求AF的长.
【分析】(1)在矩形ABCD中,有∠C=∠ABC=∠ABF+∠EBC=90°,由于AF⊥BE,所以∠AFB=∠C=90°,∠BAF=∠EBC,从而得证;
(2)在矩形ABCD中,AB=10,可知CD=AB=10,由于E为DC的中点,CE=5,由勾股定理可求得:BE=13,最后由△ABF∽△BEC得:,从而可求出答案.
【解答】解:(1)在矩形ABCD中,
有∠C=∠ABC=∠ABF+∠EBC=90°
∵AF⊥BE,
∴∠AFB=∠C=90°,
∴∠BAF=∠EBC
∴△BEC∽△ABF
(2)在矩形ABCD中,AB=10,
∴CD=AB=10,
∵E为DC的中点,
∴CE=5,
又BC=12,
在Rt△BEC中,
由勾股定理得:BE=13,
由△ABF∽△BEC得:
即:=,
∴解得:AF=
【点评】本题考查相似三角形的性质与判定,解题的关键熟练运用相似三角形的判定方法以及矩形的性质,本题属于中等题型.
25.(8分)已知二次函数y=x2﹣4x+3.
(1)该函数与x轴的交点坐标 (1,0),(3,0) ;
(2)在坐标系中,用描点法画出该二次函数的图象;
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
【分析】(1)把函数解析式整理成顶点式形式,然后写出顶点坐标即可,再令y=0,解关于x的一元二次方程即可得到与x轴的交点坐标;
(2)根据二次函数与坐标轴的交点和顶点坐标作出图象即可;
(3)①结合函数图象即可求出y<0时,自变量x的取值范围;②根据函数图象写出y的取值范围即可.
【解答】解:(1)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点坐标为(2,﹣1),
令y=0,则x2﹣4x+3=0,
解得x1=1,x2=3,
所以,与x轴的交点坐标是(1,0),(3,0);
故答案为:(1,0),(3,0);
(2)如图所示;
(3)①当1<x<3时,y<0;
②0≤x<3时,y的取值范围是﹣1≤y≤3.
【点评】本题考查了二次函数与不等式的关系,抛物线与x轴的交点问题,二次函数的性质,熟练掌握二次函数的性质以及函数图象的作法是解题的关键.
26.(7分)如图,AD是△ABC的中线,点O是AD上任一点,连接BO并延长,交AC于点E.
(1)如图1,当时,求的值;
(2)如图2,当时,求的值.
【分析】(1)过D作EDF∥AC交BE于点F,则DF是△BCD的中位线,利用中位线定理可得CE=2DF,证明△AOE≌△DOF(ASA),根据全等三角形的性质得AE=DF,即可求解;
(2)过D作EDF∥AC交BE于点F,则DF是△BCD的中位线,利用中位线定理可得CE=2DF,证明△AOE∽△DOF,根据相似三角形的性质得2AE=DF,即可求解.
【解答】解:(1)如图1,过D作DF∥AC交BE于点F.
∵DF∥AC,且AD是△ABC的中线.
∴DF是△BCE的中位线,
∴CE=2DF.
∵,
∴AO=DO,
∵DF∥AC,
∴∠EAO=∠FDO.
在△AOE和△DOF中,
,
∴△AOE≌△DOF(ASA),
∴DF=AE,
∴CE=2AE,
∴AC=3AE,
∴=;
(2)过D作EDF∥AC交BE于点F,
∵DF∥AC,且AD是△ABC的中线.
∴DF是△BCE的中位线,
∴CE=2DF.
∵,
∴,
∵DF∥AC,
∴∠EAO=∠FDO,∠AEO=∠DFO,
∴△AOE∽△DOF,
∴,
∴DF=2AE,
∴CE=4AE.
∴AC=5AE,
∴=.
【点评】本题考查了相似三角形的判定与性质,全等三角形的判定与性质,三角形中位线定理,熟练掌握三角形中位线定理是解题的关键.
27.(7分)在平面直角坐标系xOy中,抛物线y=ax2+bx+3a过点A(﹣1,0).
(1)求抛物线的对称轴;
(2)直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C.如果该抛物线与线段BC有交点,结合函数的图象,求a的取值范围.
【分析】(1)根据坐标轴上点的坐标特征代入点A的坐标,得出b=4a,则解析式为y=ax2+4ax+3a,进一步求得抛物线的对称轴;
(2)结合图形,分两种情况:①a>0;②a<0;进行讨论即可求解.
【解答】解:(1)∵抛物线y=ax2+bx+3a过点A(﹣1,0),
∴a﹣b+3a=0,
∴b=4a,
∴抛物线的解析式为y=ax2+4ax+3a,
∴抛物线的对称轴为x=﹣=﹣2;
(2)∵直线y=x+4与y轴交于点B,与该抛物线对称轴交于点C,
∴B(0,4),C(﹣2,2),
∵抛物线y=ax2+bx+3a经过点A(﹣1,0)且对称轴x=﹣2,
由抛物线的对称性可知抛物线也一定过A的对称点(﹣3,0),
①a>0时,如图1,
将x=0代入抛物线得y=3a,
∵抛物线与线段BC恰有一个公共点,
∴3a≥4,
解得a≥,
②a<0时,如图2,
将x=﹣2代入抛物线得y=﹣a,
∵抛物线与线段BC恰有一个公共点,
∴﹣a≥2,
解得a≤﹣2;
综上所述,a≥或a≤﹣2.
【点评】本题考查了二次函数的性质以及解一元一次不等式,解题的关键是熟练掌握解一元一次不等式,待定系数法求抛物线解析式.本题属于中档题,难度不大,但涉及知识点较多,需要对二次函数足够了解才能快捷的解决问题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/7/21 21:51:54;用户:菁优校本题库;邮箱:2471@xyh.cm;学号:56380052x
…
﹣2
﹣1
0
1
2
…
y
…
5
0
﹣3
﹣4
﹣3
…
x
…
…
y
…
…
x
…
﹣2
﹣1
0
1
2
…
y
…
5
0
﹣3
﹣4
﹣3
…
x
…
…
y
…
…
x
…
﹣2
﹣1
0
1
2
…
y
…
15
8
3
0
1
…
2021-2022学年北京市房山区七年级(上)期中数学试卷【含解析】: 这是一份2021-2022学年北京市房山区七年级(上)期中数学试卷【含解析】,共15页。试卷主要包含了填空题,解答题解答应写出文字说明等内容,欢迎下载使用。
北京市房山区2017届九年级(上)期中数学试卷(含解析): 这是一份北京市房山区2017届九年级(上)期中数学试卷(含解析),共35页。试卷主要包含了选择题等内容,欢迎下载使用。
2023-2024学年北京市房山区九年级上学期期中数学试卷(含解析): 这是一份2023-2024学年北京市房山区九年级上学期期中数学试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













