

所属成套资源:初中七级数学上学期期中考试卷专辑
2021-2022学年北京171中七年级(上)期中数学试卷【含解析】
展开
这是一份2021-2022学年北京171中七年级(上)期中数学试卷【含解析】,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.(2分)若a的相反数是﹣3,则a的值为( )
A.1B.2C.3D.﹣3
2.(2分)﹣的绝对值为( )
A.B.3C.﹣D.﹣3
3.(2分)有理数a、b在数轴上对应位置如图所示,则a+b的值( )
A.大于0B.小于0C.等于0D.大于a
4.(2分)5G是第五代移动通信技术,5G网络理论下载速度可以达到每秒1300000KB以上,这意味着下载一部高清电影只需要1秒.将1300000用科学记数法表示应为( )
A.13×105B.1.3×105C.1.3×106D.1.3×107
5.(2分)下列各单项式中,与﹣2mn2是同类项的是( )
A.5mnB.2n2C.3m2nD.mn2
6.(2分)下列运算正确的是( )
A.5a2﹣3a2=2B.2x2+3x2=5x4
C.3a+2b=5abD.7ab﹣6ba=ab
7.(2分)若一元一次方程ax+b=0的解是x=1,则a,b的关系为( )
A.相等B.互为相反数C.互为倒数D.互为负倒数
8.(2分)解方程时,去分母、去括号后,正确结果是( )
A.4x+1﹣10x+1=1B.4x+2﹣10x﹣1=1
C.4x+2﹣10x﹣1=6D.4x+2﹣10x+1=6
9.(2分)小亮原计划骑车以10千米/时的速度从A地去B地,在规定时间就能到达B地,但他因事比原计划晚出发15分钟,只好以15千米/时的速度前进,结果比规定时间早到6分钟,若设A,B两地间的距离为x千米,则根据题意列出的方程正确的为( )
A.+15+6B.
C.D.
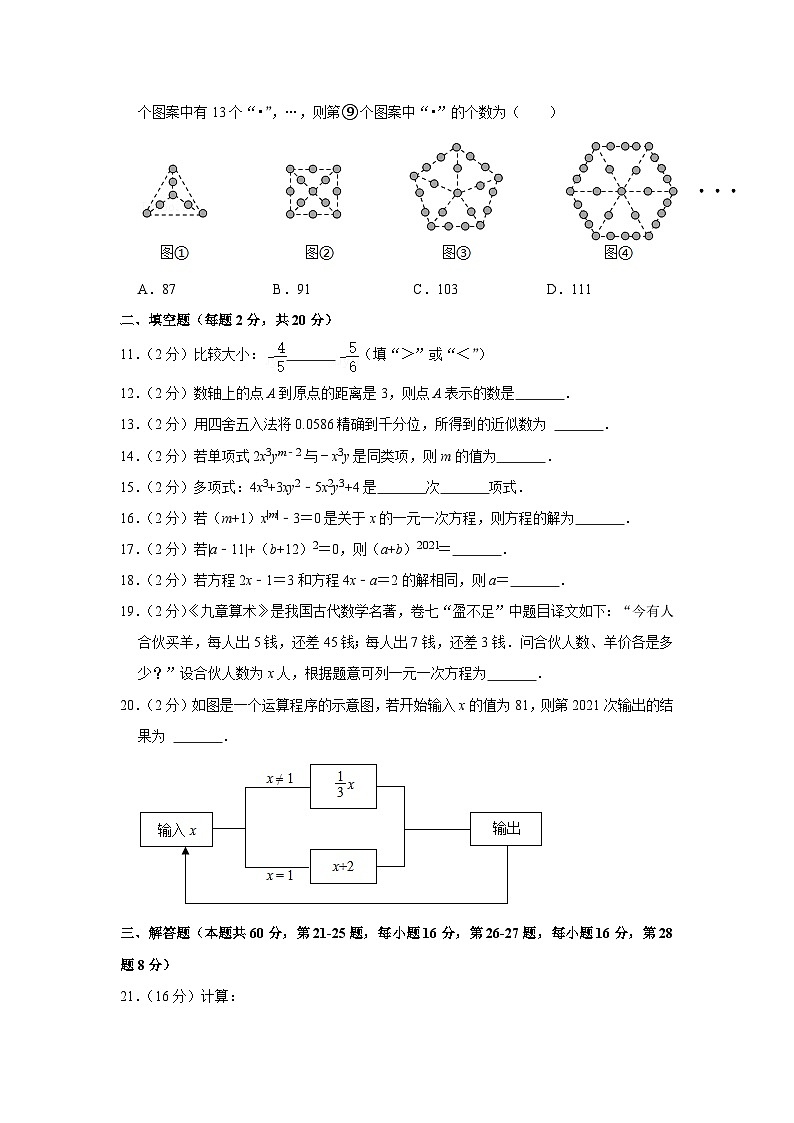
10.(2分)如图,每个图案都由若干个“•”组成,其中第①个图案中有7个“•”,第②个图案中有13个“•”,…,则第⑨个图案中“•”的个数为( )
A.87B.91C.103D.111
二、填空题(每题2分,共20分)
11.(2分)比较大小: (填“>”或“<”)
12.(2分)数轴上的点A到原点的距离是3,则点A表示的数是 .
13.(2分)用四舍五入法将0.0586精确到千分位,所得到的近似数为 .
14.(2分)若单项式2x3ym﹣2与﹣x3y是同类项,则m的值为 .
15.(2分)多项式:4x3+3xy2﹣5x2y3+4是 次 项式.
16.(2分)若(m+1)x|m|﹣3=0是关于x的一元一次方程,则方程的解为 .
17.(2分)若|a﹣11|+(b+12)2=0,则(a+b)2021= .
18.(2分)若方程2x﹣1=3和方程4x﹣a=2的解相同,则a= .
19.(2分)《九章算术》是我国古代数学名著,卷七“盈不足”中题目译文如下:“今有人合伙买羊,每人出5钱,还差45钱;每人出7钱,还差3钱.问合伙人数、羊价各是多少?”设合伙人数为x人,根据题意可列一元一次方程为 .
20.(2分)如图是一个运算程序的示意图,若开始输入x的值为81,则第2021次输出的结果为 .
三、解答题(本题共60分,第21-25题,每小题16分,第26-27题,每小题16分,第28题8分)
21.(16分)计算:
(1)(﹣6)+13﹣(﹣18)﹣20;
(2)18﹣6÷(﹣2)×(﹣);
(3);
(4).
22.(8分)化简:
(1)3x2﹣6x﹣x2﹣3+4x﹣2x2﹣1;
(2)5(x﹣2y)﹣3(2y﹣3x).
23.(4分)先化简,再求值:3(2a2b﹣4ab2)﹣(﹣3ab2+6a2b),其中a=1,b=﹣.
24.(8分)解下列方程:
(1)1﹣2(2x+3)=﹣3(2x+1);
(2).
25.(4分)2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,下表是二月份某一周的生产情况(超产为正,减产为负,单位:个).
(1)根据记录可知前三天共生产多少个口罩;
(2)产量最多的一天比产量最少的一天多生产多少个;
(3)该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总额是多少元?
26.(6分)理解与思考:
整体代换是数学的一种思想方法.例如:x2+x=0,则x2+x+1186= ;我们将x2+x作为一个整体代入,则原式=0+1186=1186.
仿照上面的解题方法,完成下面的问题:
(1)若x2+x﹣1=0,则x2+x+2021= ;
(2)如果a+b=5,求2(a+b)﹣4a﹣4b+21的值;
(3)若a2+2ab=20,b2+2ab=8,求2a2﹣3b2﹣2ab的值.
27.(6分)这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(Ⅰ)2班有61名学生,他该选择哪个方案?
(Ⅱ)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
28.(8分)在同一直线上的三点A、B、C,若满足点C到另两个点A、B的距离之比是2,则称点C是其余两点的亮点(或暗点).具体地,当点C在线段AB上时,若=2,则称点C是[A,B]的亮点;若=2,则称点C是[B,A]的亮点;当点C不在线段AB上时,若=2,称点C是[A,B]的暗点;若=2,则称点C是[B,A]的暗点.例如,如图1,在数轴上的点A、B、C、D分别表示数﹣1,2,1,0,则点C是[A,B]的亮点,又是[A,D]的暗点;点D是[B,A]的亮点,又是[B,C]的暗点.
(1)如图2,M、N为数轴上的两点,点M表示的数为﹣2,点N表示的数为4,则[M,N]的亮点表示的数是 ,[N,M]的暗点表示的数是 .
(2)如图3,数轴上的点A所表示的数为点所表示的数为﹣20,点B表示的数为40,一只电子蚂蚁P从点B出发以每秒2个单位的速度向左运动,设运动时间为t秒.
①求当t为何值时,P是[B,A]的暗点.
②求当t为何值时,P、A和B三个点中恰有一个点为其余两点的亮点.
2021-2022学年北京171中七年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题2分,共20分)
1.(2分)若a的相反数是﹣3,则a的值为( )
A.1B.2C.3D.﹣3
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.
【解答】解:a的相反数是﹣3,则a的值为3,
故选:C.
【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.
2.(2分)﹣的绝对值为( )
A.B.3C.﹣D.﹣3
【分析】根据当a是负有理数时,a的绝对值是它的相反数﹣a,可得答.
【解答】解:﹣的绝对值等于,
故选:A.
【点评】此题主要考查了绝对值,关键是掌握①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.
3.(2分)有理数a、b在数轴上对应位置如图所示,则a+b的值( )
A.大于0B.小于0C.等于0D.大于a
【分析】由数轴可知,a>0,b<0,且|b|>|a|,由此可得出答案.
【解答】解:由数轴可得:a>0,b<0,且|b|>|a|,
我们可令a=1,b=﹣2,
则a+b=﹣1<0.
故选:B.
【点评】本题考查了数轴的知识,同学们注意“赋值法”的运用,这种方法在解答选择题时很方便.
4.(2分)5G是第五代移动通信技术,5G网络理论下载速度可以达到每秒1300000KB以上,这意味着下载一部高清电影只需要1秒.将1300000用科学记数法表示应为( )
A.13×105B.1.3×105C.1.3×106D.1.3×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将1300000用科学记数法表示为:1.3×106.
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
5.(2分)下列各单项式中,与﹣2mn2是同类项的是( )
A.5mnB.2n2C.3m2nD.mn2
【分析】根据同类项的概念求解即可.
【解答】解:A、5mn与﹣2mn2所含字母相同,相同字母的指数不相同,不是同类项,故此选项不符合题意;
B、2n2与﹣2mn2所含字母不相同,不是同类项,故此选项不符合题意;
C、3m2n与﹣2mn2所含字母相同,相同字母的指数不相同,不是同类项,故此选项不符合题意;
D、mn2与﹣2mn2所含字母相同,相同字母的指数也相同,是同类项,故此选项符合题意.
故选:D.
【点评】本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:所含字母相同,相同字母的指数相同.
6.(2分)下列运算正确的是( )
A.5a2﹣3a2=2B.2x2+3x2=5x4
C.3a+2b=5abD.7ab﹣6ba=ab
【分析】根据合并同类项系数相加字母及指数不变,可得答案.
【解答】解:A、5a2﹣3a2=2a的平方,故A错误;
B、2x2+3x2=5x2,故B错误;
C、不是同类项不能合并,故C错误;
D、合并同类项系数相加字母及指数不变,故D正确;
故选:D.
【点评】本题考查了合并同类项,合并同类项系数相加字母及指数不变是解题关键,注意不是同类项不能合并.
7.(2分)若一元一次方程ax+b=0的解是x=1,则a,b的关系为( )
A.相等B.互为相反数C.互为倒数D.互为负倒数
【分析】把x=1代入方程ax+b=0得出a+b=0,即可得出答案.
【解答】解:把x=1代入方程ax+b=0得:a+b=0,
a=﹣b,
故选:B.
【点评】本题考查了一元一次方程的解的定义的应用,能理解一元一次方程的解的定义是解此题的关键.
8.(2分)解方程时,去分母、去括号后,正确结果是( )
A.4x+1﹣10x+1=1B.4x+2﹣10x﹣1=1
C.4x+2﹣10x﹣1=6D.4x+2﹣10x+1=6
【分析】方程去分母,去括号得到结果,即可做出判断.
【解答】解:方程去分母得:2(2x+1)﹣(10x+1)=6,
去括号得:4x+2﹣10x﹣1=6,
故选:C.
【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求出解.
9.(2分)小亮原计划骑车以10千米/时的速度从A地去B地,在规定时间就能到达B地,但他因事比原计划晚出发15分钟,只好以15千米/时的速度前进,结果比规定时间早到6分钟,若设A,B两地间的距离为x千米,则根据题意列出的方程正确的为( )
A.+15+6B.
C.D.
【分析】本题的等量关系是时间=路程÷速度,本题的关键语是“比规定的时间早6分钟到达B地”,由此可得出,原计划用的时间=实际用的时间+15分钟+6分钟.
【解答】解:设A、B两地间距离为x千米,
由题意得:.
故选:B.
【点评】本题主要考查了由实际问题抽象出一元一次方程,重点在于准确地找出相等关系,这是列方程的依据.
10.(2分)如图,每个图案都由若干个“•”组成,其中第①个图案中有7个“•”,第②个图案中有13个“•”,…,则第⑨个图案中“•”的个数为( )
A.87B.91C.103D.111
【分析】分别罗列前四个图案中的点数,找出规律,第n个图案的点数为(n+1)(n+2)+1,从而得出答案.
【解答】解:∵第①个图案的点数=2×3+1=7;
第②个图案的点数=3×4+1=13;
第③个图案的点数=4×5+1=21;
第④个图案的点数=5×6+1=31;
∴第⑨个图案的点数=10×11+1=111,
故选:D.
【点评】本题考查了探索规律,找出第n个图案的点数为(n+1)(n+2)+1是解题的关键.
二、填空题(每题2分,共20分)
11.(2分)比较大小: > (填“>”或“<”)
【分析】根据两有理数的大小比较法则比较即可.
【解答】解:|﹣|==,|﹣|==,
∴﹣>﹣.
故答案为:>.
【点评】本题考查了两负数的大小比较,①先求出每个数的绝对值,②根据绝对值大的反而小比较即可.
12.(2分)数轴上的点A到原点的距离是3,则点A表示的数是 ±3 .
【分析】先设出这个数为x,再根据数轴上各点到原点的距离进行解答即可.
【解答】解:设这个数是x,则|x|=3,
解得x=±3.
故答案为:±3.
【点评】本题考查的是数轴的特点,熟知数轴上各点到原点的距离的定义是解答此题的关键.
13.(2分)用四舍五入法将0.0586精确到千分位,所得到的近似数为 0.059 .
【分析】把万分位上的数字6进行四舍五入即可.
【解答】解:0.0586≈0.059(精确到千分位).
故答案为0.059.
【点评】本题考查了近似数和有效数字:近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.
14.(2分)若单项式2x3ym﹣2与﹣x3y是同类项,则m的值为 3 .
【分析】根据同类项是字母相同且相同字母的指数也相同,可得m、n的值再根据代数式求值,可得答案.
【解答】解:∵2x3ym﹣2与﹣x3y是同类项,
∴m﹣2=1,
∴m=3.
故答案为:3.
【点评】本题考查了同类项,利用同类项得出m、n的值是解题的关键.
15.(2分)多项式:4x3+3xy2﹣5x2y3+4是 五 次 四 项式.
【分析】多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数,根据这个定义即可解答.
【解答】解:多项式4x3+3xy2﹣5x2y3+4是五次四项式,
故答案为:五,四.
【点评】此题考查的是多项式的有关定义.解题的关键是掌握多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
16.(2分)若(m+1)x|m|﹣3=0是关于x的一元一次方程,则方程的解为 x= .
【分析】根据一元一次方程的定义即可求出答案.
【解答】解:由题意可知:|m|=1,
∴m=±1,
∵m+1≠0,
∴m=1,
∴原方程化为:2x﹣3=0,
∴x=,
故答案为:x=.
【点评】本题考查一元一次方程,解题的关键是熟练运用一元一次方程的定义,本题属于基础题型.
17.(2分)若|a﹣11|+(b+12)2=0,则(a+b)2021= ﹣1 .
【分析】根据非负数的性质列出算式,求出a、b的值,计算即可.
【解答】解:由题意得,a﹣11=0,b+12=0,
解得,a=11,b=﹣12,
则(a+b)2021=(11﹣12)2021=﹣1,
故答案为:﹣1.
【点评】本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.
18.(2分)若方程2x﹣1=3和方程4x﹣a=2的解相同,则a= 6 .
【分析】本题中有2个方程,且是同解方程,一般思路是:先求出不含字母系数的方程的解,再把解代入到含有字母系数的方程中,求字母系数的值.
【解答】解:解方程2x﹣1=3,
得:x=2,
把x=2代入4x﹣a=2,
得:4×2﹣a=2,
解得:a=6.
故答案为:6.
【点评】本题考查同解方程的知识,比较简单,解决本题的关键是理解方程解的定义,注意细心运算.
19.(2分)《九章算术》是我国古代数学名著,卷七“盈不足”中题目译文如下:“今有人合伙买羊,每人出5钱,还差45钱;每人出7钱,还差3钱.问合伙人数、羊价各是多少?”设合伙人数为x人,根据题意可列一元一次方程为 5x+45=7x+3 .
【分析】设合伙人数为x人,根据买羊需要的钱数不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:设合伙人数为x人,
依题意,得:5x+45=7x+3.
故答案为:5x+45=7x+3.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
20.(2分)如图是一个运算程序的示意图,若开始输入x的值为81,则第2021次输出的结果为 3 .
【分析】利用程序图进行操作计算,通过计算发现规律,从而得出结论.
【解答】解:第一次输入81,输出结果为27;
第二次输入27,输出结果为9;
第三次输入9,输出结果为3;
第四次输入3,输出结果为1;
第五次输入1,输出结果为3;
第六次输入3,输出结果为1;
•••,
可以看出:从第四次开始输入的数字以3,1为循环节开始循环,
输出的结果以1,3为循环节开始循环,
∵2021﹣3=2018,2018÷2=1009,
∴第2021次输出的结果与第5次输出的结果相同为3,
故答案为:3.
【点评】本题主要考查了求代数式的值,有理数的混合运算,本题是规律型题目,通过计算发现输入与输出出现的循环规律是解题的关键.
三、解答题(本题共60分,第21-25题,每小题16分,第26-27题,每小题16分,第28题8分)
21.(16分)计算:
(1)(﹣6)+13﹣(﹣18)﹣20;
(2)18﹣6÷(﹣2)×(﹣);
(3);
(4).
【分析】(1)先将减法转化为加法,再根据有理数加法法则计算即可;
(2)先算乘除,再算加减,同级运算,应按从左到右的顺序进行计算;
(3)根据乘法分配律计算即可;
(4)先算乘方与括号内的运算,再算乘除,最后算加减即可.
【解答】解:(1)(﹣6)+13﹣(﹣18)﹣20
=﹣6+13+18﹣20
=﹣26+31
=5;
(2)18﹣6÷(﹣2)×(﹣)
=18+3×(﹣)
=18﹣1
=17;
(3)
=﹣×16+×16﹣×16
=﹣12+14﹣8
=﹣6;
(4)
=﹣1﹣××
=﹣1﹣
=﹣1.
【点评】此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
22.(8分)化简:
(1)3x2﹣6x﹣x2﹣3+4x﹣2x2﹣1;
(2)5(x﹣2y)﹣3(2y﹣3x).
【分析】(1)利用合并同类项的法则对式子进行运算即可;
(2)先进行去括号运算,再合并同类项即可.
【解答】解:(1)3x2﹣6x﹣x2﹣3+4x﹣2x2﹣1
=(3﹣1﹣2)x2+(﹣6+4)x+(﹣3﹣1)
=﹣2x﹣4;
(2)5(x﹣2y)﹣3(2y﹣3x)
=5x﹣10y﹣6y+9x
=14x﹣16y.
【点评】本题主要考查整式的加减,解答的关键是对相应的运算法则的掌握.
23.(4分)先化简,再求值:3(2a2b﹣4ab2)﹣(﹣3ab2+6a2b),其中a=1,b=﹣.
【分析】先去括号,再合并同类项,最后代入求值.
【解答】解:原式=6a2b﹣12ab2+3ab2﹣6a2b
=﹣9ab2;
当a=1,b=﹣时,
原式=﹣9×1×(﹣)2
=﹣1.
【点评】本题考查了整式的加减及有理数的混合运算,掌握去括号法则和合并同类项法则是解决本题的关键.
24.(8分)解下列方程:
(1)1﹣2(2x+3)=﹣3(2x+1);
(2).
【分析】(1)先去括号,再把含未知数的项移到等号左边,常数项移到等号右边,然后合并,最后把未知数的系数化为1;
(2)先去分母,再去括号,移项后合并,最后把未知数的系数化为1.
【解答】解:(1)去括号,得1﹣4x﹣6=﹣6x﹣3,
移项,得﹣4x+6x=6﹣1﹣3
合并,得2x=2,
系数化为1,得x=1.
(2)去分母,得5(x﹣3)﹣2(4x+1)=10,
去括号,得5x﹣15﹣8x﹣2=10,
移项,得5x﹣8x=15+2+10,
合并,得﹣3x=27,
系数化为1,得x=﹣9.
【点评】本题考查了解一元一次方程,掌握解一元一次方程的一般步骤是解决本题的关键.解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.
25.(4分)2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,下表是二月份某一周的生产情况(超产为正,减产为负,单位:个).
(1)根据记录可知前三天共生产多少个口罩;
(2)产量最多的一天比产量最少的一天多生产多少个;
(3)该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总额是多少元?
【分析】(1)把前三天的记录相加,再加上每天计划生产量,计算即可得解;
(2)根据正负数的意义确定星期三产量最多,星期二产量最少,然后用记录相减计算即可得解;
(3)求出一周记录的和,然后根据工资总额的计算方法列式计算即可得解.
【解答】解:(1)(+100﹣200+400)+3×5000=15300(个).
故前三天共生产15300个口罩;
(2)+400﹣(﹣200)=600(个).
故产量最多的一天比产量最少的一天多生产600个;
(3)5000×7+(100﹣200+400﹣100﹣100+350+150)=35600(个),
0.2×35600=7120(元).
故本周口罩加工厂应支付工人的工资总额是7120元.
【点评】此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
26.(6分)理解与思考:
整体代换是数学的一种思想方法.例如:x2+x=0,则x2+x+1186= 1186 ;我们将x2+x作为一个整体代入,则原式=0+1186=1186.
仿照上面的解题方法,完成下面的问题:
(1)若x2+x﹣1=0,则x2+x+2021= 2022 ;
(2)如果a+b=5,求2(a+b)﹣4a﹣4b+21的值;
(3)若a2+2ab=20,b2+2ab=8,求2a2﹣3b2﹣2ab的值.
【分析】理解与思考:将x2+x=0整体代入原式进行计算;
(1)由x2+x﹣1=0可得x2+x=1,然后利用整体思想代入求值;
(2)将原式去括号,合并同类项进行化简整理,然后利用整体思想代入求值;
(3)将原式进行变形,从而利用整体思想代入求值.
【解答】解:理解与思考:
∵x2+x=0,
∴x2+x+1186=0+1186=1186,
故答案为:1186;
(1)∵x2+x﹣1=0,
∴x2+x=1,
∴原式=1+2021=2022,
故答案为:2022;
(2)原式=2a+2b﹣4a﹣4b+21
=﹣2a﹣2b+21
=﹣2(a+b)+21,
∵a+b=5,
∴原式=﹣2×5+21=﹣10+21=11,
∴2(a+b)﹣4a﹣4b+21的值为11;
(3)原式=2a2+4ab﹣3b2﹣6ab
=2(a2+2ab)﹣3(b2+2ab),
∵a2+2ab=20,b2+2ab=8,
∴原式=2×20﹣3×8=40﹣24=16,
∴2a2﹣3b2﹣2ab的值为16.
【点评】本题考查整式的加减—化简求值,掌握合并同类项(系数相加,字母及其指数不变)和去括号的运算法则(括号前面是“+”号,去掉“+”号和括号,括号里的各项不变号;括号前面是“﹣”号,去掉“﹣”号和括号,括号里的各项都变号),利用整体思想代入求值是解题关键.
27.(6分)这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(Ⅰ)2班有61名学生,他该选择哪个方案?
(Ⅱ)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
【分析】(Ⅰ)根据两种方案分别得出总费用,比较即可得出答案;
(Ⅱ)根据已知得出两种方案费用一样,进而得出等式求出即可.
【解答】解:(Ⅰ)∵方案一:61×20×0.8=976(元),
方案二:(61﹣7)×0.9×20=972(元),
∴选择方案二.
(Ⅱ)假设1班有x人,根据题意得出:
x×20×0.8=(x﹣7)×0.9×20,
解得:x=63,
答:1班有63人.
【点评】本题主要考查了一元一次方程的应用,根据已知得出关于x的等式是解题关键.
28.(8分)在同一直线上的三点A、B、C,若满足点C到另两个点A、B的距离之比是2,则称点C是其余两点的亮点(或暗点).具体地,当点C在线段AB上时,若=2,则称点C是[A,B]的亮点;若=2,则称点C是[B,A]的亮点;当点C不在线段AB上时,若=2,称点C是[A,B]的暗点;若=2,则称点C是[B,A]的暗点.例如,如图1,在数轴上的点A、B、C、D分别表示数﹣1,2,1,0,则点C是[A,B]的亮点,又是[A,D]的暗点;点D是[B,A]的亮点,又是[B,C]的暗点.
(1)如图2,M、N为数轴上的两点,点M表示的数为﹣2,点N表示的数为4,则[M,N]的亮点表示的数是 2 ,[N,M]的暗点表示的数是 ﹣8 .
(2)如图3,数轴上的点A所表示的数为点所表示的数为﹣20,点B表示的数为40,一只电子蚂蚁P从点B出发以每秒2个单位的速度向左运动,设运动时间为t秒.
①求当t为何值时,P是[B,A]的暗点.
②求当t为何值时,P、A和B三个点中恰有一个点为其余两点的亮点.
【分析】(1)设其亮点或暗点表示的未知数,再根据定义列出方程;
(2)根据新定义列出进行解答便可.
【解答】解:(1)设[M,N]的亮点表示的数是x,根据定义得:
x﹣(﹣2)=2(4﹣x),
解得x=2;
设[N,M]的暗点表示的数是k,根据定义得:
4﹣k=2(﹣2﹣k),
解得k=﹣8;
故答案为:2;﹣8;
(2)①当P为[B,A]暗点时,P在BA延长线上且PB=2PA=2×(40+20)=120,t=120÷2=60(秒);
②P为[A,B]亮点时,PA=2PB,40﹣2t﹣(﹣20)=2×2t,解得t=10;
P为[B,A]亮点时,2PA=PB,2[40﹣2t﹣(﹣20)]=2t,解得t=20;
A为[B,P]亮点时,AB=2AP,60=2[﹣20﹣(40﹣2t)],解得t=45;
A为[P,B]亮点时,2AB=AP,120=﹣20﹣(40﹣2t),解得t=90;
综上,t=10或20或45或90.
【点评】本题是新定义题,考查了一元一次方程的应用,关键是读懂定义,根据定义的特征,列出方程,把新知识转化为已经熟悉的知识来进行解答.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2022/9/29 20:48:48;用户:笑涵数学;邮箱:15699920825;学号:36906111星 期
一
二
三
四
五
六
日
增 减
+100
﹣200
+400
﹣100
﹣100
+350
+150
星 期
一
二
三
四
五
六
日
增 减
+100
﹣200
+400
﹣100
﹣100
+350
+150
相关试卷
这是一份2021-2022学年北京七中七年级(上)期中数学试卷【含解析】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年北京八十中七年级(上)期中数学试卷【含解析】,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年北京161中七年级(上)期中数学试卷【含解析】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








