






新高考数学一轮复习课件第2章函数导数及其应用第8讲 函数与方程(含解析)
展开对于函数 y=f(x),把使 f(x)=0 的实数 x 叫做函数 y=
(2)函数零点与方程解的关系
方程 f(x)=0 有实数解⇔函数 y=f(x)的图象与 x 轴有交
点⇔函数 y=f(x)有零点.
(3)函数零点存在定理
如果函数 y=f(x)满足:①在区间[a,b]上的图象是一条连续不断的曲线;②f(a)·f(b)<0;则函数 y=f(x)在区间(a,b)内至少有一个零点,即存在 c∈(a,b),使得 f(c)=0,这个 c 也就是方程 f(x)=0 的解.
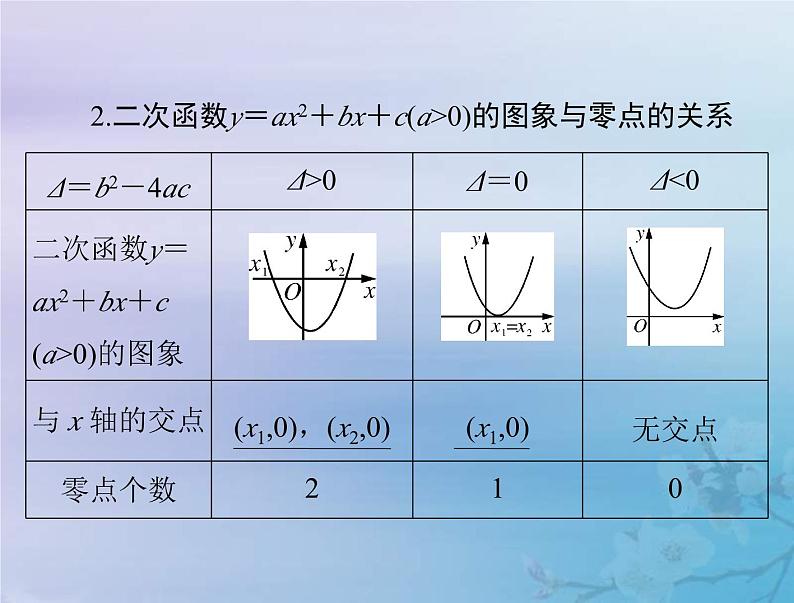
2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
(1)若函数 f(x)(图象是连续不断的)在定义域上是单调函数,则 f(x)至多有一个零点.函数的零点不是一个“点”,而是方程 f(x)=0 的实根.
(2)由函数 y=f(x)(图象是连续不断的)在闭区间[a,b]上有零点不一定能推出 f(a)·f(b)<0,如图 2-8-1 所示,所以f(a)·f(b)<0 是 y=f(x)在闭区间[a,b]上有零点的充分不必要条件.
题组一 走出误区1.若函数 y=f(x)在区间[a,b]上的图象为连续不断的一
条曲线,则下列说法正确的是(
A.若 f(a)f(b)>0,不存在实数 c∈(a,b)使得 f(c)=0B.若 f(a)f(b)>0,有可能存在实数 c∈(a,b)使得 f(c)=0C.若 f(a)f(b)<0,存在且只存在一个实数 c∈(a,b)使得f(c)=0D.若 f(a)f(b)<0,有可能不存在实数 c∈(a,b)使得f(c)=0答案:B
题组二 走进教材2.(教材改编题)函数 f(x)的图象如图 2-8-2 所示,它与 x轴有 4 个不同的公共点.给出下列四个区间,不能用二分法
求出函数 f(x)零点的区间是(A.[-2.1,-1]B.[1.9,2.3]C.[4.1,5]D.[5,6.1]答案:B
3.(教材改编题)已知函数 f(x)与 g(x)的图象在 R 上不间断,由下表知函数 y=f(x)-g(x)在下列区间内一定有零点
题组三 真题展现4.(2019 年全国Ⅲ)函数 f(x)=2sin x-sin 2x 在[0,2π]的
考点一 函数零点所在区间的判定[例 1](1)设 f(x)=ln x+x-2,则函数 f(x)的零点所在的
区间为(A.(0,1)C.(2,3)
B.(1,2)D.(3,4)
解析:因为 y=ln x 与 y=x-2 在(0,+∞)上都单调递
所以 f(x)=ln x+x-2 在(0,+∞)上单调递增,又 f(1)=ln 1+1-2=-1<0,f(2)=ln 2>0,
根据函数零点存在定理,可知函数 f(x)=ln x+x-2 有
唯一零点,且零点在区间(1,2)内.
【题后反思】确定函数 f(x)的零点所在区间的常用
(1)利用函数零点存在定理:首先看函数 y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数 y=f(x)在区间(a,b)内必有零点.
(2)数形结合法:通过作出函数图象,观察图象与 x 轴
在给定区间上是否有交点来判断.
【变式训练】1.若 a
A.(0,1)C.(2,3)
考点二 确定函数零点的个数1.函数f(x)=2x+x3-2在区间(0,1)内的零点个数是
解析:∵f(0)f(1)=(-1)×1=-1<0,且函数在定义域上单调递增且连续,∴函数 f(x)在区间(0,1)内有且只有 1 个零点.答案:B
2.函数f(x)=3x|ln x|-1的零点个数为( )
【题后反思】函数零点个数的判定有下列几种方法(1)直接求零点:令f(x)=0,如果能求出解,那么有几
(2)函数零点存在定理:利用该定理不仅要求函数在[a,b]上是连续的曲线,且 f(a)·f(b)<0,还必须结合函数的图象和性质(如单调性)才能确定函数有多少个零点.
(3)作出两个函数图象,看其交点的个数有几个,其中交点的横坐标有几个不同的值,就有几个不同的零点.
考点三 根据函数零点个数求参数
通性通法:根据函数零点的情况求参数有三种常用方
(1)直接法:直接根据题设条件构建关于参数的不等
式,再通过解不等式确定参数范围.
(2)分离参数法:先将参数分离,转化成求函数值域问
(3)数形结合法:先对解析式变形,在同一平面直角坐
标系中作出函数的图象,然后数形结合求解.
[例 2](1)(2021 年宜宾期末)已知函数 f(x)=ln x+ax 在
上有两个零点,则 a 的取值范围是________.
解析:令 x2-1-(4+x)≥1,得 x≤-2 或 x≥3,令 x2-1-(4+x)<1,得-2
函数 y=f(x)+k 有 3 个零点,等价于函数 y=f(x)的图
象与直线 y=-k 有 3 个交点,
根据函数图象可得-1<-k≤2,即-2≤k<1.
g(x)=f(x)-x-a 有且只有两个不同的零点,则实数 a 的取
解析:根据题意,作出 f(x)的图象如图 D14 所示:
令 g(x)=0,得 f(x)=x+a,
所以要使函数 g(x)=f(x)-x-a 有且只有两个不同的
所以只需函数 f(x)的图象与直线 y=x+a 有两个不同
根据图象可得实数 a 的取值范围为(-1,+∞).故选
⊙数形结合法求解函数零点问题
解析:∵f(x)为偶函数,故 f(2-x)=f(x-2),∴f(x+2)=f(x-2),故 f(x)的周期为 4,
象如图 2-8-5 所示,
∵f(x)-lga(x+2)=0 有 3 个不同的解,∴f(x)的图象与y=lga(x+2)的图象有3个不同的交点,
直观想象是指借助几何直观想象和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的思想过程.函数的零点问题可以转化为两个函数图象的交点问题,可以通过作图分析图象的特征、图象间的关系解决.
【高分训练】1.(2021年衡水中学调研)方程|x2-2x|=a2+1(a>0)的
解的个数是(A.1C.3
解析:(数形结合法)∵a>0,∴a2+1>1.而 y=|x2-2x|的图象如图 D15,
∴y=|x2-2x|的图象与 y=a2+1 的图象总有两个交点.
即方程有 2 个解.故选 B.
m,n,则(A.mn=1C.0
2.若函数f(x)=|lgax|-2-x(a>0且a≠1)的两个零点是
新高考数学一轮复习课件第2章函数导数及其应用第7讲 函数的图象(含解析): 这是一份新高考数学一轮复习课件第2章函数导数及其应用第7讲 函数的图象(含解析),共50页。PPT课件主要包含了描点法作图,2对称变换,3伸缩变换,4翻折变换,名师点睛,中心对称,的图象相同,答案A,答案C,题组三真题展现等内容,欢迎下载使用。
2025年高考数学一轮复习-第二章 函数-第8讲 函数与方程【课件】: 这是一份2025年高考数学一轮复习-第二章 函数-第8讲 函数与方程【课件】,共42页。PPT课件主要包含了必备知识自主排查,核心考点师生共研等内容,欢迎下载使用。
2025版高考数学一轮总复习第2章函数概念与基本初等函数Ⅰ第8讲函数与方程课件: 这是一份2025版高考数学一轮总复习第2章函数概念与基本初等函数Ⅰ第8讲函数与方程课件,共60页。PPT课件主要包含了fx=0,fc=0,一分为二,函数的零点,-12,f025等内容,欢迎下载使用。












