






新高考数学一轮复习课件第2章函数导数及其应用第1讲 函数的概念及其表示(含解析)
展开2.函数的定义域、值域和对应关系
(1)在函数 y=f(x),x∈A 中,x 叫做自变量,x 的取值集合 A 叫做函数的定义域;与 x 的值相对应的 y 值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.(2)如果两个函数的定义域相同,并且对应关系完全一
致,则这两个函数为相等函数.
表示函数的常用方法有解析法、图象法和列表法.
(1)若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.(2)分段函数的定义域等于各段函数的定义域的并集,其值域等于各段函数的值域的并集,分段函数虽由几个部分组成,但它表示的是一个函数.
直线 x=a(a 是常数)与函数 y=f(x)的图象有 0 个或 1
题组一 走出误区 1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若 A=R,B={x|x>0},f:x→y=|x|,其对应是从 A
(2)若两个函数的定义域与值域相同,则这两个函数相
(3)已知 f(x)=5(x∈R),则 f(x2)=25.(
(4)函数 f(x)的图象与直线 x=1 最多有一个交点.(答案:(1)× (2)× (3)× (4)√
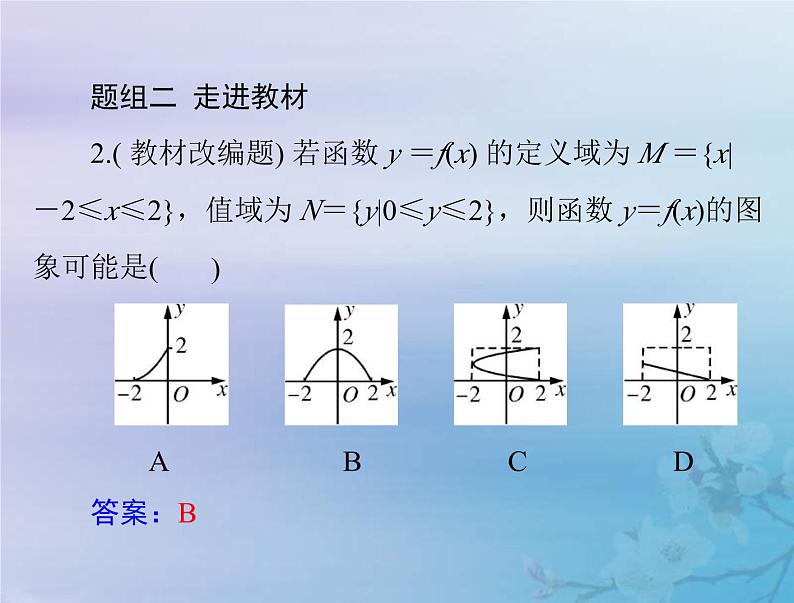
题组二 走进教材2.( 教材改编题) 若函数 y =f(x) 的定义域为 M ={x|-2≤x≤2},值域为 N={y|0≤y≤2},则函数 y=f(x)的图
3.(教材改编题)下列函数中,与函数 y=x+1 是相等函
题组三 真题展现4.(2019 年上海春季)下列函数中,值域为[0,+∞)的
考点一 求函数的定义域
考向 1 求具体函数的定义域
通性通法:求给定解析式的函数定义域的方法
求给定解析式的函数的定义域,其实质就是以函数解析式中所含式子(运算)有意义为准则,列出不等式或不等式组求解;对于实际问题,定义域应使实际问题有意义.
[例 1]求下列函数的定义域:
考向 2 抽象函数的定义域
通性通法:求抽象函数定义域的方法
(1)若已知函数 f(x)的定义域为[a,b],则复合函数 f(g(x))
的定义域可由不等式 a≤g(x)≤b 求出.
(2)若已知函数 f(g(x))的定义域为[a,b],则 f(x)的定义
域为 g(x)在 x∈[a,b]上的值域.
[例 2](1)已知函数 f(x)的定义域为(-1,0),则函数
f(2x+1)的定义域为(
(2)已知函数 f(2x+1)的定义域为(-1,0),则函数 f(x)
解析:f(2x+1)的定义域为(-1,0),即-1
A.(-9,+∞)C.[-9,+∞)
B.(-9,1)D.[-9,1)
考点二 求函数的解析式
[例 3](1)已知f(x+1)=x2-1,求f(x)的解析式.
解:(法一) f(x+1)=x2-1=(x+1)2-2x-2=(x+1)2-
可令t=x+1,则有f(t)=t2-2t.故f(x)=x2-2x. (法二)令x+1=t,则x=t-1.代入原式,有f(t)=(t-1)2-1=t2-2t,∴f(x)=x2-2x.
(3)已知 f(x)是一次函数,且满足 3f(x+1)-2f(x-1)=2x+17,求 f(x)的解析式.解:设 f(x)=ax+b(a≠0),则 3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+5a+b,即 ax+5a+b=2x+17 不论 x 为何值都成立.
(4)已知 f(x)+2f(-x)=x+1,求 f(x)的解析式.
解:因为 f(x)+2f(-x)=x+1,对任意 x∈R 都成立,所以用-x 替换 x,得 f(-x)+2f(x)=-x+1,由以上两式
【题后反思】求函数解析式的常用方法
(1)待定系数法:若已知函数的类型,可用待定系数法.(2)换元法:已知复合函数 f(g(x))的解析式,可用换元
法,此时要注意新元的取值范围.
式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出 f(x).
【变式训练】1.已知函数 f(x)=ax-b(a>0),且 f(f(x))=4x-3,则 f(2)=________.
2.若 f(x)满足 2f(x)+f(-x)=3x,则 f(x)=________.
所以将 x 用-x 替换,得 2f(-x)+f(x)=-3x,②由①②解得 f(x)=3x.
解析:因为 2f(x)+f(-x)=3x,①
考点三 分段函数考向 1 分段函数求值
考向 2 分段函数与方程、不等式问题
(1)根据分段函数解析式求函数值,首先确定自变量的值属于哪个区间,其次选定相应的解析式代入求解.(2)已知函数值或函数的取值范围求自变量的值或范围时,应根据每一段的解析式分别求解,但要注意检验所求自变量的值或范围是否符合相应段的自变量的取值范围.
特别提醒:当分段函数的自变量范围不确定时,应分
【考法全练】1.(考向 1)(2021 年富阳月考)已知函数 f(x)=
f(x)=x-x2,要使函数 y=f(x)-c 的图象与 x 轴恰有两个公共点,只需方程 f(x)-c=0 有两个不相等的实数根即可,即函数 y=f(x)的图象与直线 y=c 有两个不同的交点即可,画出函数 y=f(x)的图象与直线 y=c,不难得出答案 B.答案:B
新高考数学一轮复习课件第2章函数导数及其应用第8讲 函数与方程(含解析): 这是一份新高考数学一轮复习课件第2章函数导数及其应用第8讲 函数与方程(含解析),共44页。PPT课件主要包含了答案B,图2-8-3,答案12,图D12,图D13,答案3,个解就有几个零点,答案D,图2-8-4,答案1等内容,欢迎下载使用。
新高考数学一轮复习课件第2章函数导数及其应用第7讲 函数的图象(含解析): 这是一份新高考数学一轮复习课件第2章函数导数及其应用第7讲 函数的图象(含解析),共50页。PPT课件主要包含了描点法作图,2对称变换,3伸缩变换,4翻折变换,名师点睛,中心对称,的图象相同,答案A,答案C,题组三真题展现等内容,欢迎下载使用。
新高考数学一轮复习课件第2章函数导数及其应用第6讲 对数与对数函数(含解析): 这是一份新高考数学一轮复习课件第2章函数导数及其应用第6讲 对数与对数函数(含解析),共58页。PPT课件主要包含了对数的概念,反函数,名师点睛,图2-6-1,数逐渐增大,题组一走出误区,答案ABC,BbD2ab,图2-6-2,答案B等内容,欢迎下载使用。












