数学拓展模块一（上册）5.1 复数的概念和意义获奖ppt课件

这是一份数学拓展模块一（上册）5.1 复数的概念和意义获奖ppt课件PPT课件主要包含了情境导入，复数的概念，探索新知，典型例题，巩固练习，复数的几何意义，1z3，归纳总结，布置作业等内容，欢迎下载使用。

很久以前,人们认为一元二次方程x²+1=0 是无解的.但是,随着对数系的深人研究,人们逐渐意识到应该存在一个数,它就是该方程的解.
  依照引入负数,使方程x+1=0有解的方法,是否可以引入一个数使方程x²+1=0有解呢？
既然i是一个数,那么它与实数就可以进行运算.实数b与i的乘积写成 bi,实数a与bi的和写成a+bi. 
把形如a+bi (a、b∈R)的数称为复数,其中a称为复数的实部, b称为复数的虚部. 
复数通常用小写英文字母z、w……表示,如z=a+bi.全体复数构成的集合称为复数集,用C表示,即C={z|z= a+bi,a,b∈R}. 
当b=0时,复数a+bi就是实数; 当b≠0时,复数a+bi称为虚数; 当a=0且b≠0时,复数称为纯虚数.
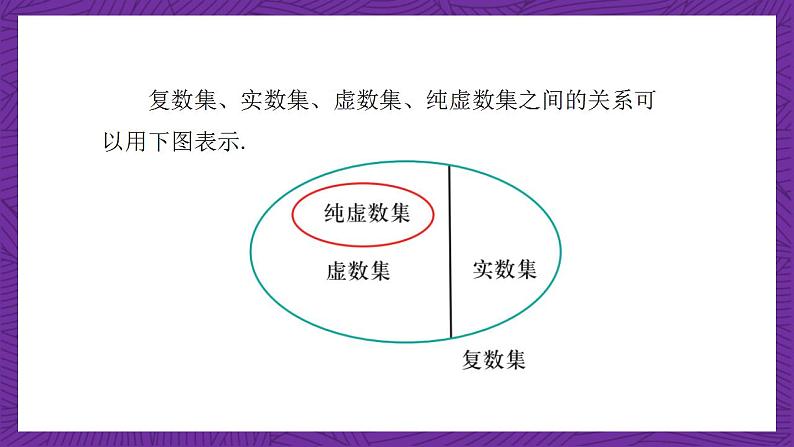
全体虚数构成的集合称为虚数集,全体纯虚数构成的集合称为纯虚数集,它们与实数集、复数集之间具有怎样的关系？
复数集、实数集、虚数集、纯虚数集之间的关系可以用下图表示.
如果两个复数a+bi与c+di的实部与虚部分别相等,就称这两个复数相等，记作 a+bi=c+di. 即,如果a、b、c、d都是实数,那么 a+bi=c+di⇔ a=c且b=d. 特别地, a+bi=0 ⇔ a=0且b=0.
从两个复数相等的定义可知,复数a+bi与有序实数对(a,b)之间是一一对应的.
例2 求满足下列条件的实数a和b. （1）(a+2b)-i=6a+(a-b)i；
1. 写出下列复数的实部和虚部.
我们知道,任意一个实数都可以用数轴上的点来表示,那么复数可否用点来表示呢？
由复数相等的定义,复数z=a+bi与有序实数对(a,b)之间是一一对应的.而有序实数对(a,b)与平面直角坐标系中的点也是 一一对应的．因此,复数集里的复数与平面直角坐标系中的点可以建立一一对应关系,即复数可以用平面直角坐标系中的点来表示.
如图所示,复数z=a+bi可以用平面直角坐标系中的点Z(a,b)来表示.用来表示复数的平面称为复平面,直角坐标系中的x轴称为实轴,y轴(除去原点)称为虚轴.显然,实轴上的点都表示实数;虚轴上的点都表示纯虚数. 
例如,复平面内的原点O(0,0)表示实数O,点A(1,0)表示实数,点B(0,-1)表示纯虚数-i,点D(1,-1 )表示复数 1- i. 
例3  在复平面内，画出表示复数 3-i、4、2i 的点和向量. 
一般地,如果两个复数的实部相等,虚部互为相反数,那么这两个复数互为共轭复数. 
设复数z在复平面内对应的点为 Z,问满足下列条件的点Z的集合是什么图形？
两个实数可以比较大小,试问两个复数可以比较大小吗？
1.书面作业：完成课后习题和《学习指导与练习》；2.查漏补缺：根据个人情况对课堂学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.