中职高教版（2021·十四五）第4章 立体几何4.4 平面与平面的位置关系优秀课件ppt

这是一份中职高教版（2021·十四五）第4章 立体几何4.4 平面与平面的位置关系优秀课件ppt，共47页。PPT课件主要包含了情境导入，探索新知，两平面平行，典型例题，巩固练习，二面角，两平面垂直，归纳总结，布置作业等内容，欢迎下载使用。

一般地,当两个平面有一条公共直线时,称两个平面相交;当两个平面没有公共点时,称两个平面平行.
观察发现,两个平面之间的位置关系有两种:相交和平行.事实上,根据公理3可知,当两个平面有一个公共点时,这两个平面相交于一条直线.
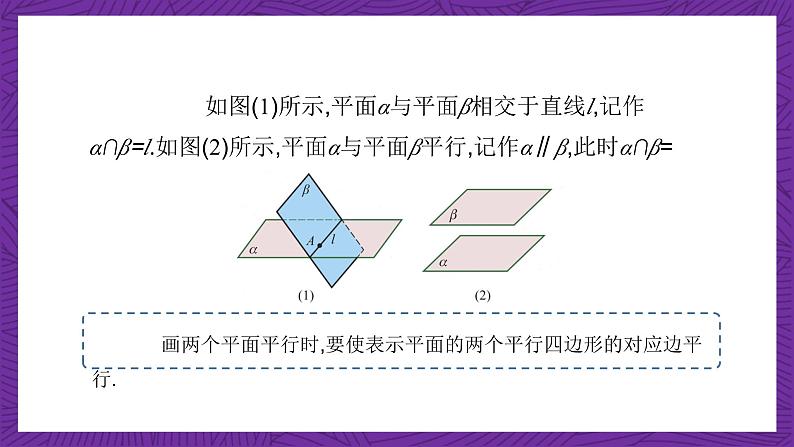
如图(1)所示,平面α与平面β相交于直线l,记作α∩β=l.如图(2)所示,平面α与平面β平行,记作α∥β,此时α∩β=
画两个平面平行时,要使表示平面的两个平行四边形的对应边平行.
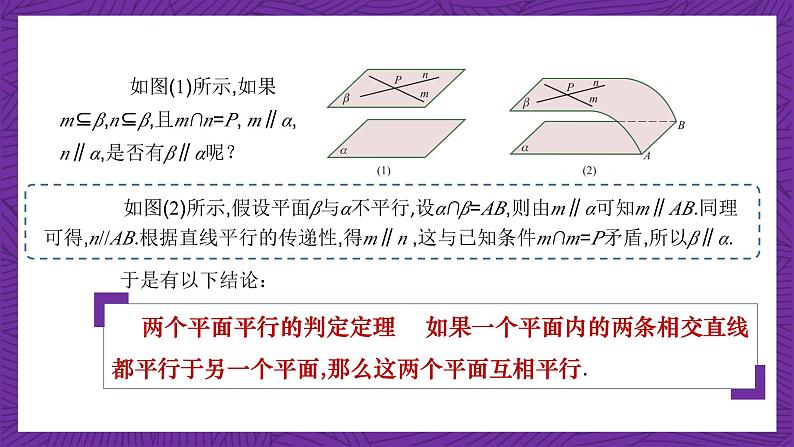
如图(1)所示,如果m⊆β,n⊆β,且m∩n=P, m∥α, n∥α,是否有β∥α呢？
如图(2)所示,假设平面β与α不平行,设α∩β=AB,则由m∥α可知m∥AB.同理可得,n//AB.根据直线平行的传递性,得m∥n ,这与已知条件m∩m=P矛盾,所以β∥α. 
于是有以下结论：
两个平面平行的判定定理 如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面互相平行.
既然可以用直线与平面平行、直线与直线平行判定平面与平面平行,那么能否利用平面与平面的平行来判定直线与平面平行、直线与直线平行呢？
如果两个平面平行,那么其中一个平面内的直线必平行于另一个平面.也就是说,如果α∥β, l⊆α,那么l ∥β.
两个平面平行的性质定理  如果两个平行平面同时和第三个平面相交,那么两条交线互相平行. 
例2 证明：如果一条直线与两个平行平面中的一个平面垂直，那么它也与另一个平面垂直. 已知: α //β,l⊥α,如图所示. 求证: l⊥β.
1. 在底面为矩形的四棱柱ABCD-A1B1C1D1中,平面AD1与平面A1C1的位置关系是 ,平面AB1与平面DC1的位置关系是 .
3. 在长方体ABCD-A1B1C1D1中,E、F、G、H分别是A1B1、AB、AD、A1D1的中点,求证:平面EFGH∥平面BB1D1D.
打开笔记本计算机时,显示屏的开合程度不同,键盘与屏幕所在平面的相对位置就不同,如图所示.怎样来描述这种不同呢？
观察可知,显示屏的开合程度可以用角度来描述.
  平面内的一条直线把这个平面分成两部分,其中的每一部分都称为半平面. 从一条直线出发的两个半平面所组成的图形称为二面角,这条直线称为二面角的棱,这两个半平面称为二面角的面.
根据二面角的不同摆放位置,常常把二面角画成图所示图形.
当二面角的棱为l,两个面分别为α、β时,二面角记为α-l-β.图(4)所示的二面角也可记为A-BD-C. 
如图,平面角∠AOB的大小就是二面角α-l-β的大小.
  如图所示,在二面角α-l-β的棱l上任取一点O,分别在两个面内作垂直于校的射线OA、OB,射线 OA、OB 所成的最小正角称为这个二面角的平面角. 
可以用二面角的平面角的大小度量二面角的大小.
我们己经知道了两条直线所成的角和直线与平面所成的角的定义,那么,两个平面所成的角怎样定义呢？
1. 己知二面角α-l-β,C∈α ,D∈β,AC⊥AB,AD⊥AB,垂足均为A,则二面角α-AB-β的平面角是 .  2. 已知正方体 ABCD-A1B1C1D1,试找出二面角A1-BD-A 与二面角A1-BD-C 的一个平面角,并分析二者之间的大小关系. 
3.判断下列说法是否正确. （1）两个相交平面所成的角的取值范围是 而二面角的取值范围是[0,π]； （2）在正方体 ABCD-A1B1C1D1中,∠D1AB1是二面角D1-AA1-B1的平面角；  （3）分别在二面角的两个面内取一条直线,使两条直线相交,则相交直线所成的角是二面角的平面角. 
4. 己知等腰ΔABC的腰长为5cm,底边长为8cm. 现沿着底边上的高AD 对折,折后 求二面角B-AD-C的大小. 5.在长方体ABCD-A1B1C1D1中,求二面角B1-CD-A的大小.
  当两个平面所成的角是 时,称这两个平面互相垂直.
我们知道,利用直线与直线垂直可以判定直线与平面垂直.类似地,也可以利用直线与平面垂直来判定平面与平面垂直. 
  两个平面垂直的判定定理  如果一个平面经过另一个平面的条垂线, 那么这两个平面互相垂直.
两平面垂直的性质定理  如果两个平面互相垂直, 那么在一个平面内垂直于交线的直线垂直于另一个平面 .
  5. 在墙上挂一个镜框,为了使镜框下沿与地面平行,可先拿两根等长的木棍紧靠壁放在地上,并让木棍与墙角线垂直,再把镜框下沿放到木棍上. 试说明这一方法据的数学原理是什么. 
1.书面作业：完成课后习题和《学习指导与练习》；2.查漏补缺：根据个人情况对课堂学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.