新高考数学二轮复习巩固练习20 圆锥曲线经典难题之一类面积、面积比问题的通性通法研究（2份打包，原卷版+解析版）

这是一份新高考数学二轮复习巩固练习20 圆锥曲线经典难题之一类面积、面积比问题的通性通法研究（2份打包，原卷版+解析版），文件包含新高考数学二轮复习巩固练习20圆锥曲线经典难题之一类面积面积比问题的通性通法研究原卷版doc、新高考数学二轮复习巩固练习20圆锥曲线经典难题之一类面积面积比问题的通性通法研究解析版doc等2份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。

1、三角形面积问题
模型一：基本方法
模型二：分割三角形
模型三：三角形面积坐标表示
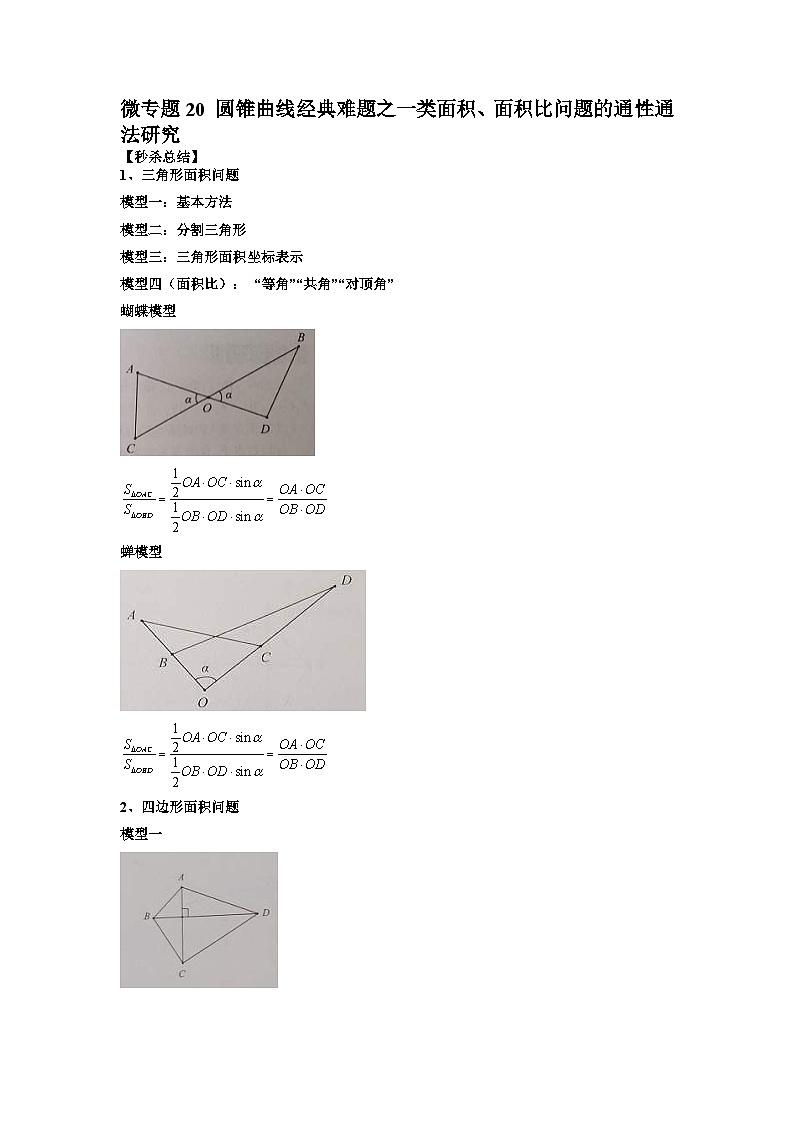
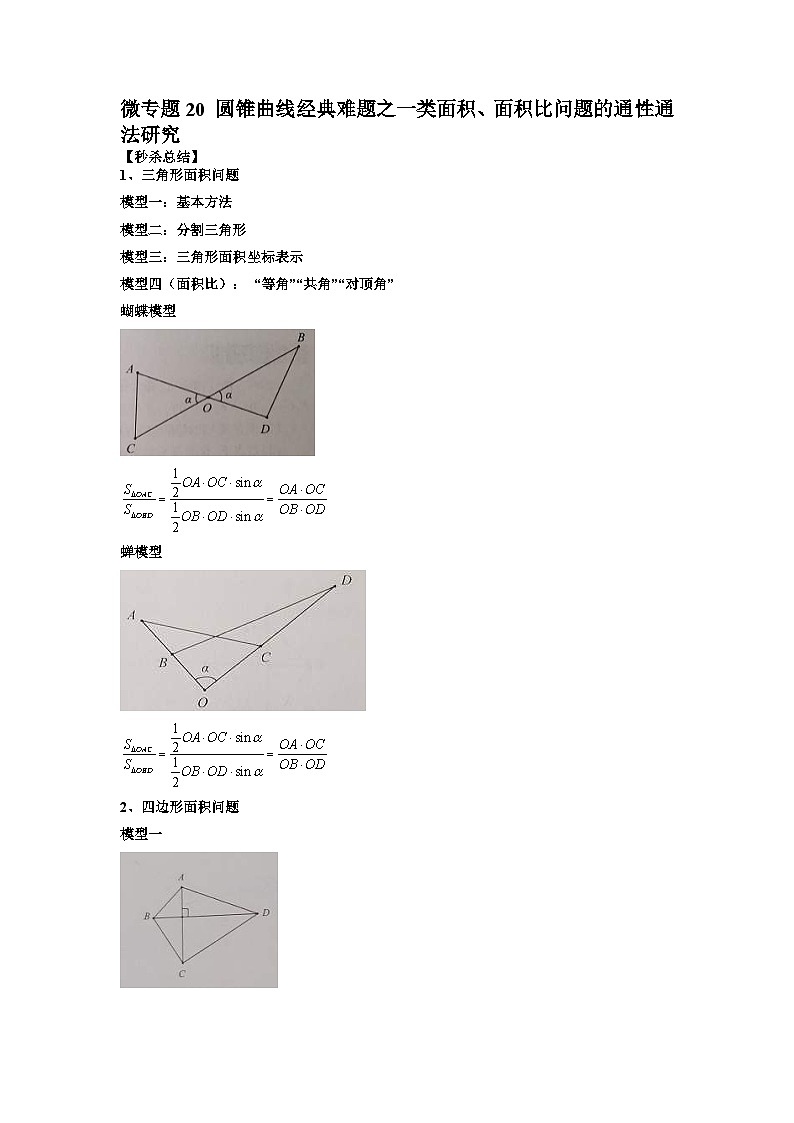
模型四（面积比）： “等角”“共角”“对顶角”
蝴蝶模型
SKIPIF 1 < 0
蝉模型
SKIPIF 1 < 0
2、四边形面积问题
模型一
SKIPIF 1 < 0
模型二
SKIPIF 1 < 0
模型三
SKIPIF 1 < 0
3、圆锥曲线中取值范围问题的五种求解策略：
（1）利用圆锥曲线的几何性质或判别式构造不等关系，从而确定参数的取值范围；
（2）利用已知参数的范围，求新的参数的范围，解这类问题的核心是建立两个参数之间的等量关系；
（3）利用隐含的不等关系建立不等式，从而求出参数的取值范围；
（4）利用已知的不等关系建立不等式，从而求出参数的取值范围；
（5）利用求函数值域的方法将待求量表示为其他变量的函数，求其值域，从而确定参数的取值范围.
4、圆锥曲线中的最值问题解决方法一般分两种：
一是几何法，特别是用圆锥曲线的定义和平面几何的有关结论来求最值；
二是代数法，常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题，然后利用基本不等式、函数的单调性或三角函数的有界性等求最值．
【典型例题】
例1．（2023·宁夏银川·一模）如图，已知椭圆 SKIPIF 1 < 0 ，曲线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴的交点为 SKIPIF 1 < 0 ，过坐标原点 SKIPIF 1 < 0 的直线 SKIPIF 1 < 0 与相交于 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别与 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 .
(1)证明：以 SKIPIF 1 < 0 为直径的圆经过点 SKIPIF 1 < 0 ；
(2)记 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的取值范围.
例2．（2023·浙江·模拟预测）如图，点A，B是椭圆 SKIPIF 1 < 0 与曲线 SKIPIF 1 < 0 的两个交点，其中点A与C关于原点对称，过点A作曲线 SKIPIF 1 < 0 的切线与x轴交于点D．记△ABC与△ABD的面积分别是 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)证明： SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最大值．
例3．（2023·河南·一模（理））已知点F为椭圆 SKIPIF 1 < 0 的右焦点，椭圆上任意一点到点F距离的最大值为3，最小值为1.
（1）求椭圆C的标准方程；
（2）若M为椭圆C上的点，以M为圆心， SKIPIF 1 < 0 长为半径作圆M，若过点 SKIPIF 1 < 0 可作圆M的两条切线 SKIPIF 1 < 0 ( SKIPIF 1 < 0 为切点)，求四边形 SKIPIF 1 < 0 面积的最大值.
例4．（2023·天津·南开中学二模）已知椭圆 SKIPIF 1 < 0 的左右焦点分别是 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，离心率为 SKIPIF 1 < 0 ，点P在椭圆E上，且 SKIPIF 1 < 0 的面积的最大值为 SKIPIF 1 < 0 .
（1）求椭圆C的方程；
（2）直线l过椭圆C右焦点 SKIPIF 1 < 0 ，交该椭圆于A､B两点，AB中点为Q，射线OQ交椭圆于P，记 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，求直线l的方程.
例5．（2023·全国·高三专题练习）已知椭圆 SKIPIF 1 < 0 过点 SKIPIF 1 < 0 ，且离心率为 SKIPIF 1 < 0 ．
(1)求椭圆C的方程；
(2)设 SKIPIF 1 < 0 ，直线l与椭圆C交于 SKIPIF 1 < 0 两点，且 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 （O为坐标原点）的面积S最大时，求直线l的方程．
例6．（2023·全国·高三专题练习）过椭圆 SKIPIF 1 < 0 上任意一点 SKIPIF 1 < 0 作直线 SKIPIF 1 < 0
(1)证明: SKIPIF 1 < 0 ;
(2)若 SKIPIF 1 < 0 为坐标原点，线段 SKIPIF 1 < 0 的中点为 SKIPIF 1 < 0 ，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 的平行线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 两点，求 SKIPIF 1 < 0 面积的最大值.
例7．（2023·全国·高三专题练习）椭圆 SKIPIF 1 < 0 经过点 SKIPIF 1 < 0 且离心率为 SKIPIF 1 < 0 ；直线 SKIPIF 1 < 0 与椭圆 SKIPIF 1 < 0 交于A， SKIPIF 1 < 0 两点，且以 SKIPIF 1 < 0 为直径的圆过原点.
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)若过原点的直线 SKIPIF 1 < 0 与椭圆 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 两点，且 SKIPIF 1 < 0 ，求四边形 SKIPIF 1 < 0 面积的最大值.
例8．（2023·全国·高三专题练习）如图， 椭圆 SKIPIF 1 < 0 的右焦点为 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 的一动直线 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 转动，并且交椭圆于 SKIPIF 1 < 0 两点， SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 的中点.
(1)求点 SKIPIF 1 < 0 的轨迹 SKIPIF 1 < 0 的方程;
(2)在 SKIPIF 1 < 0 的方程中， 令 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
①设轨迹 SKIPIF 1 < 0 的最高点和最低点分别为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 为何值时， SKIPIF 1 < 0 为正三角形?
②确定 SKIPIF 1 < 0 的值， 使原点距直线 SKIPIF 1 < 0 最远， 此时， 设 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交点为 SKIPIF 1 < 0 ，当直线 SKIPIF 1 < 0 绕点 SKIPIF 1 < 0 转动到什么位置时， SKIPIF 1 < 0 的面积最大， 并求出面积的最大值?
例9．（2023·全国·高三专题练习）在平面直角坐标系中 SKIPIF 1 < 0 ，椭圆 SKIPIF 1 < 0 的离心率为 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在椭圆 SKIPIF 1 < 0 上.
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)设椭圆 SKIPIF 1 < 0 的左､右顶点分别为 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 过点 SKIPIF 1 < 0 ，且交椭圆于 SKIPIF 1 < 0 两点（异于 SKIPIF 1 < 0 两点），记直线 SKIPIF 1 < 0 的斜率为 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 的斜率为 SKIPIF 1 < 0 .
①求 SKIPIF 1 < 0 的值；
②设 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最大值.
【过关测试】
1．（2023·黑龙江哈尔滨·高三哈尔滨三中校考阶段练习）已知椭圆 SKIPIF 1 < 0 ,经过点 SKIPIF 1 < 0 ,离心率为 SKIPIF 1 < 0 .
(1)求椭圆 SKIPIF 1 < 0 的标准方程;
(2)点 SKIPIF 1 < 0 在椭圆 SKIPIF 1 < 0 上,若直线 SKIPIF 1 < 0 的斜率分别为 SKIPIF 1 < 0 ,且满足 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 面积的最大值.
2．（2023·山东菏泽·高三统考期末）已知点 SKIPIF 1 < 0 和直线 SKIPIF 1 < 0 ： SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 过直线 SKIPIF 1 < 0 上的动点M且与直线 SKIPIF 1 < 0 垂直，线段 SKIPIF 1 < 0 的垂直平分线l与直线 SKIPIF 1 < 0 相交于点P．
(1)求点P轨迹C的方程；
(2)过点F的直线l与C交于 SKIPIF 1 < 0 两点．若C上恰好存在三个点 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 的面积等于 SKIPIF 1 < 0 ，求l的方程．
3．（2023·河南信阳·高三信阳高中校考期末）已知椭圆 SKIPIF 1 < 0 的上､下顶点分别为 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在椭圆内，且直线 SKIPIF 1 < 0 分别与椭圆 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 两点，直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴交于点 SKIPIF 1 < 0 ．已知 SKIPIF 1 < 0 ．
(1)求椭圆 SKIPIF 1 < 0 的标准方程；
(2)设 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的取值范围．
4．（2023·上海闵行·高三上海市七宝中学校考期末）已知椭圆 SKIPIF 1 < 0 的左右焦点 SKIPIF 1 < 0 分别是双曲线 SKIPIF 1 < 0 的左右顶点，且椭圆 SKIPIF 1 < 0 的上顶点到双曲线 SKIPIF 1 < 0 的渐近线的距离为 SKIPIF 1 < 0 .设 SKIPIF 1 < 0 是第一象限内 SKIPIF 1 < 0 上的一点， SKIPIF 1 < 0 的延长线分别交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 .
(1)求椭圆 SKIPIF 1 < 0 的方程.
(2)求 SKIPIF 1 < 0 面积的取值范围.
(3)设 SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 的内切圆半径，求 SKIPIF 1 < 0 的最大值.
5．（2023·北京·高三校考期末）已知椭圆 SKIPIF 1 < 0 的离心率为 SKIPIF 1 < 0 ，以椭圆 SKIPIF 1 < 0 的任意三个顶点为顶点的三角形的面积是 SKIPIF 1 < 0 ．
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)设 SKIPIF 1 < 0 为原点，A为椭圆的左顶点， SKIPIF 1 < 0 是椭圆 SKIPIF 1 < 0 上不同于点A的两点，且直线 SKIPIF 1 < 0 的斜率之积等于 SKIPIF 1 < 0 ．求 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的面积比值．
6．（2023·全国·高三专题练习）仿射变换是处理圆锥曲线综合问题中求点轨迹的一类特殊而又及其巧妙的方法，它充分利用了圆锥曲线与圆之间的关系，具体解题方法为将 SKIPIF 1 < 0 由仿射变换得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则椭圆 SKIPIF 1 < 0 变为 SKIPIF 1 < 0 ，直线的斜率与原斜率的关系为 SKIPIF 1 < 0 ，然后联立圆的方程与直线方程通过计算韦达定理算出圆与直线的关系，最后转换回椭圆即可．已知椭圆 SKIPIF 1 < 0 的离心率为 SKIPIF 1 < 0 ，过右焦点 SKIPIF 1 < 0 且垂直于 SKIPIF 1 < 0 轴的直线与 SKIPIF 1 < 0 相交于 SKIPIF 1 < 0 两点且 SKIPIF 1 < 0 ，过椭圆外一点 SKIPIF 1 < 0 作椭圆 SKIPIF 1 < 0 的两条切线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，切点分别为 SKIPIF 1 < 0 ．
(1)求证：点 SKIPIF 1 < 0 的轨迹方程为 SKIPIF 1 < 0 ；
(2)若原点 SKIPIF 1 < 0 到 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的距离分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，延长表示距离 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的两条直线，与椭圆 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 两点，过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于 SKIPIF 1 < 0 ，试求：点 SKIPIF 1 < 0 所形成的轨迹与 SKIPIF 1 < 0 所形成的轨迹的面积之差是否为定值，若是，求出此定值；若不是，请求出变化函数．
7．（2023·湖北·高三统考期末）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为椭圆 SKIPIF 1 < 0 ： SKIPIF 1 < 0 的左、右焦点.点 SKIPIF 1 < 0 为椭圆上一点，当 SKIPIF 1 < 0 取最大值 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)点 SKIPIF 1 < 0 为直线 SKIPIF 1 < 0 上一点（且 SKIPIF 1 < 0 不在 SKIPIF 1 < 0 轴上），过点 SKIPIF 1 < 0 作椭圆 SKIPIF 1 < 0 的两条切线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，切点分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 轴的对称点为 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 轴于点 SKIPIF 1 < 0 .设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最大值.
8．（2023·全国·高三对口高考）如题图，已知点 SKIPIF 1 < 0 是 SKIPIF 1 < 0 轴左侧（不含 SKIPIF 1 < 0 轴）一点，抛物线 SKIPIF 1 < 0 上存在不同的两点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的中点均在抛物线 SKIPIF 1 < 0 上．
(1)设 SKIPIF 1 < 0 中点为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，证明： SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 是曲线 SKIPIF 1 < 0 上的动点，求 SKIPIF 1 < 0 面积的最小值．
9．（2023·全国·高三专题练习）已知椭圆 SKIPIF 1 < 0 ，离心率为 SKIPIF 1 < 0 ，其左右焦点分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在椭圆内，P为椭圆上一个动点，且 SKIPIF 1 < 0 的最大值为5．
(1)求椭圆C的方程；
(2)在椭圆C的上半部分取两点M，N（不包含椭圆左右端点），且 SKIPIF 1 < 0 ，求四边形 SKIPIF 1 < 0 的面积．
10．（2023·江苏扬州·高三校考期末）已知过点 SKIPIF 1 < 0 的椭圆 SKIPIF 1 < 0 ： SKIPIF 1 < 0 上的点到焦点的最大距离为3.
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)已知过椭圆 SKIPIF 1 < 0 ： SKIPIF 1 < 0 上一点 SKIPIF 1 < 0 的切线方程为 SKIPIF 1 < 0 .已知点M为直线 SKIPIF 1 < 0 上任意一点，过M点作椭圆 SKIPIF 1 < 0 的两条切线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为切点， SKIPIF 1 < 0 与 SKIPIF 1 < 0 （O为原点）交于点D，当 SKIPIF 1 < 0 最小时求四边形 SKIPIF 1 < 0 的面积.
11．（2023·北京西城·高三统考期末）如图，已知椭圆 SKIPIF 1 < 0 的一个焦点为 SKIPIF 1 < 0 ，离心率为 SKIPIF 1 < 0 ．
(1)求椭圆E的方程；
(2)过点 SKIPIF 1 < 0 作斜率为k的直线交椭圆E于两点A，B， SKIPIF 1 < 0 的中点为M．设O为原点，射线 SKIPIF 1 < 0 交椭圆E于点C．当 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的面积相等时，求k的值．
12．（2023·全国·高三专题练习）已知抛物线 SKIPIF 1 < 0 的焦点与椭圆 SKIPIF 1 < 0 的右焦点重合，直线 SKIPIF 1 < 0 与圆 SKIPIF 1 < 0 相切．
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)设不过原点的直线 SKIPIF 1 < 0 与椭圆 SKIPIF 1 < 0 相交于不同的两点A，B，M为线段AB的中点，O为坐标原点，射线OM与椭圆 SKIPIF 1 < 0 相交于点P，且O点在以AB为直径的圆上，记 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的取值范围．
13．（2023春·江苏镇江·高三校考开学考试）已知椭圆 SKIPIF 1 < 0 的左、右焦点分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，上顶点为A，钝角三角形 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，斜率为 SKIPIF 1 < 0 的直线 SKIPIF 1 < 0 交椭圆C于P，Q两点.当直线 SKIPIF 1 < 0 经过 SKIPIF 1 < 0 ，A两点时，点 SKIPIF 1 < 0 到直线 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 .
(1)求椭圆C的标准方程；
(2)设O为坐标原点，当直线 SKIPIF 1 < 0 的纵截距不为零时，试问是否存在实数k，使得
SKIPIF 1 < 0 为定值?若存在，求出此时 SKIPIF 1 < 0 面积的最大值；若不存在，请说明理由.
14．（2023·全国·高三专题练习）已知抛物线 SKIPIF 1 < 0 ： SKIPIF 1 < 0 的焦点为 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 引圆 SKIPIF 1 < 0 ： SKIPIF 1 < 0 的一条切线，切点为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)求抛物线 SKIPIF 1 < 0 的方程；
(2)过圆M上一点A引抛物线C的两条切线，切点分别为P，Q，是否存在点A使得 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ？若存在，求点A的个数；否则，请说明理由.
15．（2023·江苏扬州·高三扬州中学校考阶段练习）已知点 SKIPIF 1 < 0 是焦点为F的抛物线C： SKIPIF 1 < 0 上一点．
(1)求抛物线C的方程；
(2)设点P是该抛物线上一动点，点M，N是该抛物线准线上两个不同的点，且 SKIPIF 1 < 0 的内切圆方程为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 面积的最小值．
16．（2023春·湖北襄阳·高三襄阳市襄州区第一高级中学校考开学考试）已知抛物线 SKIPIF 1 < 0 上一点 SKIPIF 1 < 0 到准线的距离为 SKIPIF 1 < 0 ，焦点为 SKIPIF 1 < 0 ，坐标原点为 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 与抛物线 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两点（与 SKIPIF 1 < 0 点均不重合）．
(1)求抛物线 SKIPIF 1 < 0 的方程；
(2)若以 SKIPIF 1 < 0 为直径的圆过原点 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的面积之和的最小值．
17．（2023·全国·高三专题练习）已知椭圆 SKIPIF 1 < 0 短轴的两个顶点与右焦点的连线构成等边三角形，直线 SKIPIF 1 < 0 与圆 SKIPIF 1 < 0 相切.
(1)求椭圆 SKIPIF 1 < 0 的方程；
(2)过点 SKIPIF 1 < 0 作两条互相垂直的直线 SKIPIF 1 < 0 ，与椭圆 SKIPIF 1 < 0 分别交于 SKIPIF 1 < 0 四点，如图，求四边形 SKIPIF 1 < 0 的面积的取值范围.
18．（2023·上海·高三专题练习）如图， SKIPIF 1 < 0 为坐标原点，椭圆 SKIPIF 1 < 0 的左、右焦点分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，离心率为 SKIPIF 1 < 0 ；双曲线 SKIPIF 1 < 0 的左、右焦点分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，离心率为 SKIPIF 1 < 0 ，已知 SKIPIF 1 < 0 ， 且 SKIPIF 1 < 0 SKIPIF 1 < 0 过 SKIPIF 1 < 0 作 SKIPIF 1 < 0 的不垂直于 SKIPIF 1 < 0 轴的弦 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点，直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 交于 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两点.
(1)求 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的方程；
(2)若四边形 SKIPIF 1 < 0 为平行四边形，求直线 SKIPIF 1 < 0 的方程；
(3)求四边形 SKIPIF 1 < 0 面积的最小值.
19．（2023·全国·高三专题练习）设A、B两点的坐标分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，直线AD，BD相交于点D，且它们斜率之积为 SKIPIF 1 < 0 ．
(1)求点D的轨迹方程C；
(2)若斜率为k(其中k≠0)的直线l过点G(1,0)，且与曲线C交于点E、F，弦EF的中点为H，O为坐标原点，直线OH与曲线C交于点M、N，求四边形MENF的面积S的取值范围．
20．（2023·全国·高三专题练习）椭圆 SKIPIF 1 < 0 上有两点 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．点 SKIPIF 1 < 0 关于椭圆中心 SKIPIF 1 < 0 的对称点为点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在椭圆内部 SKIPIF 1 < 0 ． SKIPIF 1 < 0 是椭圆的左焦点， SKIPIF 1 < 0 是椭圆的右焦点．
(1)若点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，求点 SKIPIF 1 < 0 坐标；
(2)是否存在一个点 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 ，若满足求出点 SKIPIF 1 < 0 坐标，若不存在请说明理由；
(3)设 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的取值范围．