初中数学北师大版（2024）九年级上册1 菱形的性质与判定优秀同步达标检测题

这是一份初中数学北师大版（2024）九年级上册1 菱形的性质与判定优秀同步达标检测题，文件包含专题01菱形的性质与判定3个知识点10种题型2个易错点3种考法原卷版docx、专题01菱形的性质与判定3个知识点10种题型2个易错点3种考法解析版docx等2份试卷配套教学资源，其中试卷共71页， 欢迎下载使用。

倍速学习五种方法
【方法一】 脉络梳理法
知识点1：菱形的定义
知识点2：菱形的性质（重难点）
知识点3：菱形的判定（重难点）
【方法二】 实例探索法
题型1：利用菱形的性质计算
题型2：利用菱形的性质进行证明
题型3：求菱形的面积
题型4：利用菱形的轴对称性解决最小值问题
题型5：证明四边形为菱形
题型6：菱形的判定与性质的综合应用
题型7：与菱形有关的探究性问题
题型8：菱形中的动点问题
题型9：一题多解-菱形证明
题型10：菱形中的翻折与旋转
【方法三】 差异对比法
易错点1菱形的面积公式应用出错
易错点2 不理解菱形的几种判定方法而导致错误
【方法四】 仿真实战法
考法1：菱形的性质
考法2：菱形的判定
考法3：菱形的判定、性质的综合
【方法五】 成果评定法
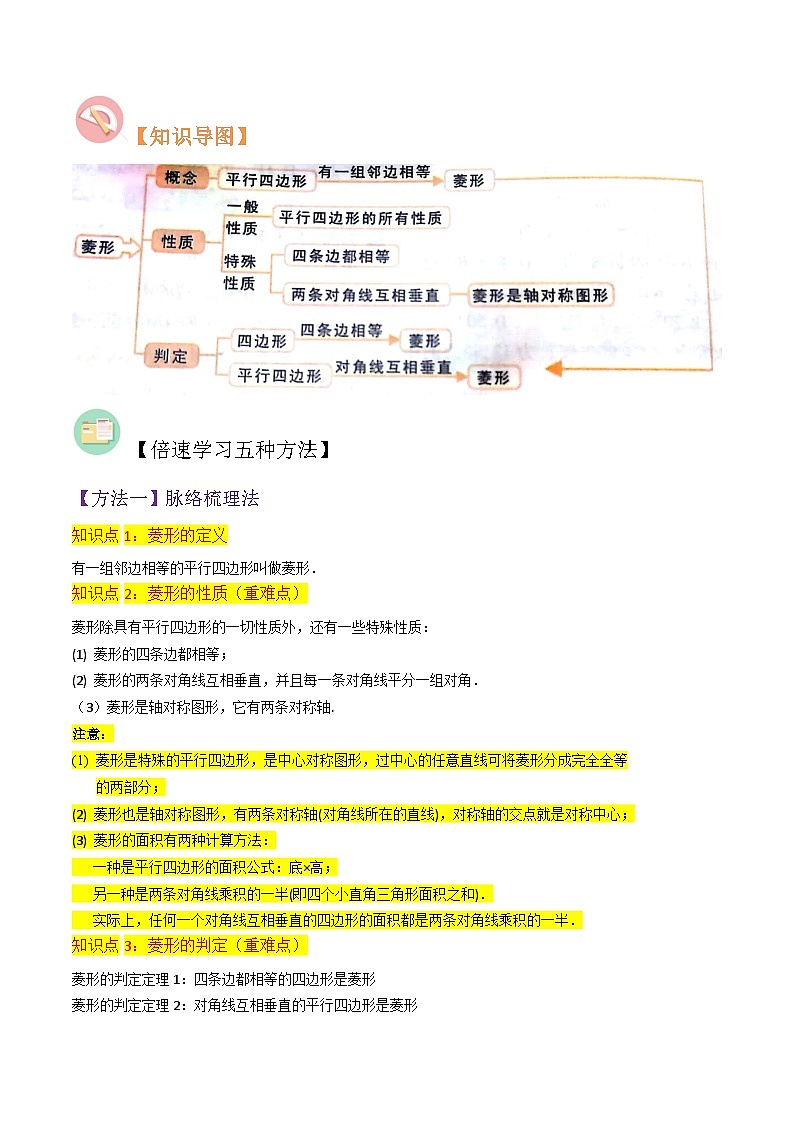
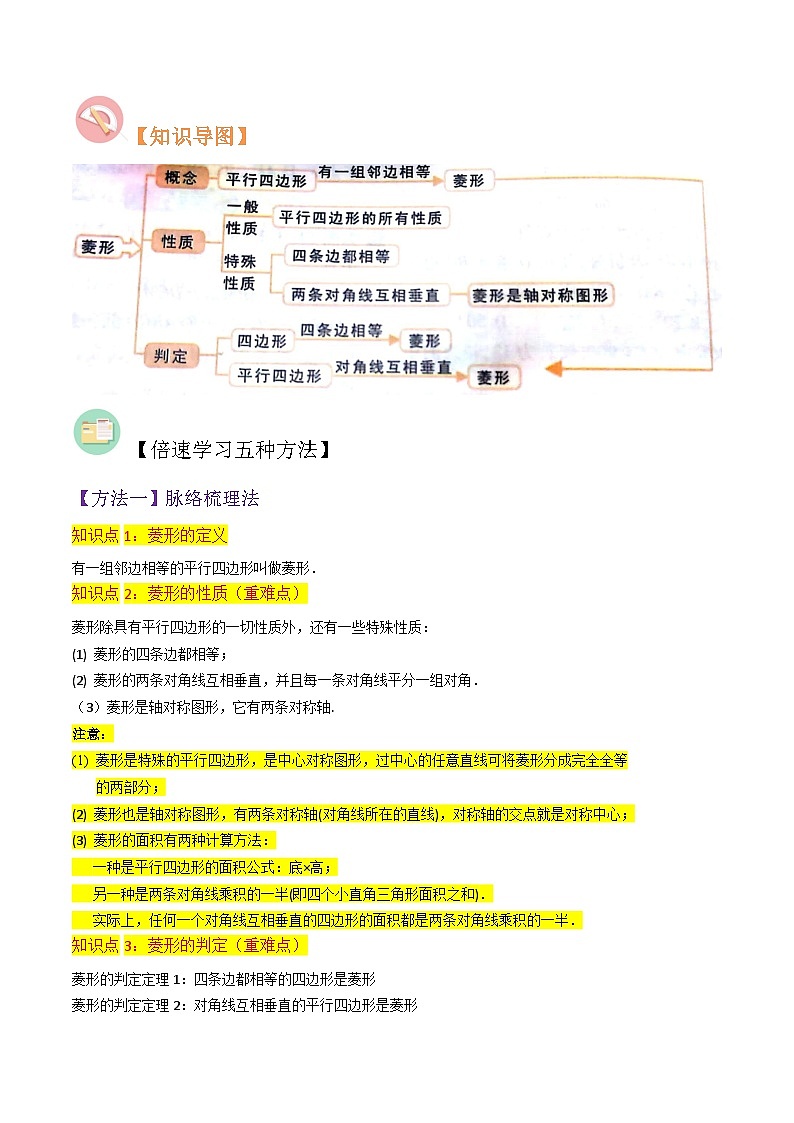
【知识导图】
【倍速学习五种方法】
【方法一】脉络梳理法
知识点1：菱形的定义
有一组邻边相等的平行四边形叫做菱形．
知识点2：菱形的性质（重难点）
菱形除具有平行四边形的一切性质外，还有一些特殊性质：
(1) 菱形的四条边都相等；
(2) 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．
（3）菱形是轴对称图形，它有两条对称轴.
注意：
菱形是特殊的平行四边形，是中心对称图形，过中心的任意直线可将菱形分成完全全等
的两部分；
(2) 菱形也是轴对称图形，有两条对称轴(对角线所在的直线)，对称轴的交点就是对称中心；
(3) 菱形的面积有两种计算方法：
一种是平行四边形的面积公式：底×高；
另一种是两条对角线乘积的一半(即四个小直角三角形面积之和)．
实际上，任何一个对角线互相垂直的四边形的面积都是两条对角线乘积的一半．
知识点3：菱形的判定（重难点）
菱形的判定定理1：四条边都相等的四边形是菱形
菱形的判定定理2：对角线互相垂直的平行四边形是菱形
定义判定：有一组邻边相等的平行四边形是菱形.
要点诠释：前一种方法是在四边形的基础上加上四条边相等.后两种方法都是在平行四边形的基础上外加一个条件来判定菱形，
例1.下列命题中，真命题是 ( )
A．一组对边平行且有一组邻边相等的四边形是平行四边形
B．等边三角形既是轴对称图形又是中心对称图形
C．对角线互相垂直平分的四边形是菱形
【方法二】实例探索法
题型1：利用菱形的性质计算
例2（1）菱形的两条对角线长的比是，边长为10厘米，菱形的面积是_________；
（2）菱形的两条对角线长的比是2:3，面积是12cm2，则它的两条对角线的长分别是_____cm、_____cm，该菱形的周长是_______cm．
例3.（1）菱形有一个内角为，一条较短的对角线长为6，则菱形的边长为 _________；
（2）如图，在菱形中，，，则 ．
O
例4.如图所示，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF，求∠CDF的度数．
A
B
C
D
E
F
题型2：利用菱形的性质进行证明
例5．已知：如图，四边形ABCD是菱形，F是AB上一点，DF交AC于E．求证：∠AFD=∠CBE．
题型3：求菱形的面积
例6.如图所示，在菱形ABCD中，AC＝8，BD＝10．
求：(1)AB的长．(2)菱形ABCD的面积．
题型4：利用菱形的轴对称性解决最小值问题
例7.如图，菱形ABCD的边长为4 cm，且∠ABC＝60°，E是BC的中点，P点在BD上，则PE+PC的最小值为________
题型5：证明四边形为菱形
例8.如图， 中，，，平分交于，
交于．求证：四边形是菱形．
题型6：菱形的判定与性质的综合应用
例9.如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，AE∥CD，CE∥AB，连接DE交AC于点O．
（1）证明：四边形ADCE是菱形；
（2）证明：DE=BC；
（3）若∠B=60°，BC=6，求菱形ADCE的高（计算结果保留根号）．

题型7：与菱形有关的探究性问题
例10.已知△ABC是等边三角形，点D是射线BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交射线AB、AC于点F、G，连接BE．
（1）如图1所示，当点D在线段BC上时，
①试说明：△AEB≌△ADC
②探究四边形BCGE是怎样特殊的四边形，并说明理由．
（2）如图2所示，当点D在BC的延长线上时，探究四边形BCGE是怎样特殊的四边
形，并说明理由．
（3）在（2）的情况下，当点D运动到什么位置时，四边形BCGE是菱形？并说明理
由．
A
B
C
D
E
F
G
A
B
C
D
G
E
图1 图2
题型8：菱形中的动点问题
例11.如图，菱形ABCD的边长为2，BD＝2，E，F分别是边AD，CD上的两个动点且满足AE+CF＝2．
（1）判断△BEF的形状，并说明理由；
（2）设△BEF的面积为S，求S的取值范围．
题型9：一题多解-菱形证明
例12.如图：在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F．求证：四边形AEFG是菱形．
题型10：菱形中的翻折与旋转
例13．（2022秋·江苏扬州·九年级统考期末）如图，在菱形中，，．折叠该菱形，使点A落在边上的点M处，折痕分别与边交于点E、F．当点M在上时，长的最大值为__________．
例14．（2023·广东东莞·东莞市厚街海月学校校考模拟预测）如图，是菱形边上的高，将绕着点顺时针旋转120°到的位置，若五边形面积为，则的长度为（ ）
A．5B．C．10D．
【方法三】差异对比法
易错点1菱形的面积公式应用出错
例15.一个菱形的边长为5，一条对角线长是6，则该菱形的面积为（ ）
A．8B．12C．16D．24
易错点2 不理解菱形的几种判定方法而导致错误
例16.下列命题中，真命题是 ( )
A．一组对边平行且有一组邻边相等的四边形是平行四边形
B．等边三角形既是轴对称图形又是中心对称图形
C．对角线互相垂直平分的四边形是菱形
【方法四】 仿真实战法
考法1：菱形的性质
1．（2022•温州）如图，在菱形ABCD中，AB＝1，∠BAD＝60°．在其内部作形状、大小都相同的菱形AENH和菱形CGMF，使点E，F，G，H分别在边AB，BC，CD，DA上，点M，N在对角线AC上．若AE＝3BE，则MN的长为 ．
考法2：菱形的判定
2．（2022•嘉兴）小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD．求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．
若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．
考法3：菱形的判定、性质的综合
3．（2021•绍兴）数学兴趣小组同学从“中国结”的图案（图1）中发现，用相同的菱形纵向排列放置，可得到更多的菱形．如图2，用2个相同的菱形放置，得到3个菱形．下面说法正确的是（ ）
A．用3个相同的菱形放置，最多能得到6个菱形
B．用4个相同的菱形放置，最多能得到16个菱形
C．用5个相同的菱形放置，最多能得到27个菱形
D．用6个相同的菱形放置，最多能得到41个菱形
【方法五】 成果评定法
一、单选题
1．（2023·浙江绍兴·统考一模）如图，某学校门口的伸缩门在伸缩的过程中，四边形始终是菱形，则下列结论不一定正确的是（ ）
A．B．C．AB=ADD．AB=CD
2．（2023·浙江嘉兴·统考一模）如图，在菱形中，，则的度数为（ ）
A．B．C．D．
3．（2023·天津西青·统考一模）如图，在平面直角坐标系中，菱形的四个顶点都在坐标轴上，且菱形边长为2，，则点的坐标为（ ）
A．B．C．D．
4．（2023春·河南南阳·九年级统考阶段练习）如图，在菱形中，对角线，菱形的面积为24，则菱形的周长为（ ）
A．5B．10C．20D．30
5．（2023·广东东莞·东莞市厚街海月学校校考模拟预测）如图，是菱形边上的高，将绕着点顺时针旋转120°到的位置，若五边形面积为，则的长度为（ ）
A．5B．C．10D．
6．（2023·河南郑州·郑州外国语中学校考一模）如图所示，边长为4的菱形中，对角线与交于点O，P为中点，Q为中点，连接，则的长为（ ）
A．B．C．D．
7．（2023·天津河西·统考模拟预测）如图，菱形中的顶点O，A的坐标分别为，，点C在x轴的正半轴上，则点B的坐标为（ ）
A．B．C．D．
二、填空题
8．（2022秋·江苏扬州·九年级统考期末）如图，在菱形中，，．折叠该菱形，使点A落在边上的点M处，折痕分别与边交于点E、F．当点M在上时，长的最大值为__________．
9．（2023·山西晋中·统考模拟预测）如图，在菱形中，对角线与相交于点，，，则菱形的面积为_____．
10．（2023·广西梧州·统考一模）如图，在平面直角坐标系中，菱形的顶点，点P是对角线上的一个动点，已知，则的最小值是_________________
11．（2023·山东德州·校考一模）如图，在菱形中，，，，分别是边和对角线上的动点，且，则的最小值为______．
12．（2023春·广东茂名·九年级校联考阶段练习）以菱形的对角线交点O为原点，对角线、所在直线为坐标轴，建立如图所示的直角坐标系，的中点E的坐标为，则的中点F的坐标为__．
13．（2023·江苏常州·校考二模）如图，在菱形中，，．点P为边上一点，且不与点C，D重合，连接，过点A作，且，连接，则四边形的面积为______．
14．（2023·浙江台州·统考一模）关于某个四边形的三个特征描述：①对角线互相垂直；②对角线互相平分；③一组邻边相等．选择其中两个作为条件，另一个作为结论．若该命题是假命题，则选择的条件是____________．（填序号）
三、解答题
15．（2023·山东滨州·统考一模）如图，四边形是菱形，点为对角线的中点，点在的延长线上，，垂足为，点在的延长线上，，垂足为，
(1)若，求证：四边形是菱形；
(2)若，的面积为24，求菱形的面积．
16．（2023·云南临沧·统考一模）如图，在中，，、分别为、的中点，连接并延长至点，且，点为直线上的一个动点．
(1)求证：四边形为菱形．
(2)若，菱形的面积为24，求的最小值．
17．（2023·北京·模拟预测）如图：在菱形中，对角线、交于点，过点作于点，延长至点，使＝，连接．
(1)求证：四边形是矩形；
(2)若，，求的长．
18．（2023·广东珠海·统考一模）如图，矩形的对角线， 相交于点O，且， ．
(1)求证：四边形是菱形．
(2)若，求四边形的面积．
19．（2023·浙江宁波·统考一模）图1，图2都是由边长为1的正方形构成的网格，每个小正方形的顶点称为格点，线段的端点均在格点上，分别按要求画出图形．
(1)在图1中画出等腰直角三角形，点C在格点上．
(2)在图2中画出以为边的菱形，点D，E在格点上．
20．（2023·四川资阳·统考一模）如图，在中，O为的中点，过点O作交于点，交于点F．
(1)求证：四边形是菱形；
(2)若，求的长．
21．（2023·山东临沂·统考一模）【操作发现】在实践活动课上，同学们对菱形和轴对称进行了研究．如图，在菱形中，为锐角，为中点，连接，点，关于直线的对称点分别为点，，连接，．请补全图形解答下列问题：
(1)直线与有怎样的位置关系，请说明理由；
(2)延长交于点．线段与相等吗？若相等，给出证明；若不相等，请说明理由；
【拓展应用】
(3)在（2）的条件下，连接，请探究的度数，并说明理由．
22．（2023·陕西宝鸡·统考二模）如图，在平面直角坐标系中，菱形的顶点的坐标为，顶点、分别在第二、三象限，交轴负半轴于点，，求顶点的坐标．
23．（2023·江苏苏州·模拟预测）如图，四边形是平行四边形，延长，，使得，连接，．
(1)求证：；
(2)连接，已知，，当___________时，四边形是菱形．
24．（2023春·江西吉安·九年级江西省泰和中学校考阶段练习）如图，菱形中，，，点为边上一动点（不与点，重合），将沿翻折，得到，交菱形的一边于点，所在直线交所在直线于点．
(1)如图（1），当点在上方时，的长的取值范围为_________．
(2)若，如图（2），求证：．
(3)在点移动的过程中，判断是否成立，并说明理由．
25．（2023·江苏无锡·模拟预测）如图，在四边形中，，对角线，交于点，，且平分，过点作交的延长线于点．
(1)求证：四边形是菱形；
(2)若，，求的面积．
26．（2023·江苏扬州·校联考一模）如图，在平行四边形中，E、F是对角线上的点，且，连接．
(1)求证：；
(2)连接，若，求证：四边形是菱形．
小惠：
证明：∵AC⊥BD，OB＝OD，
∴AC垂直平分BD．
∴AB＝AD，CB＝CD，
∴四边形ABCD是菱形．
小洁：
这个题目还缺少条件，需要补充一个条件才能证明．