
黑龙江省哈尔滨师范大学青冈实验中学校2023-2024学年高二下学期期末考试数学试题
展开一、单项选择题(本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求。)
1.已知集合 ,则 ( )
A.B.C.D.
2.已知命题,则为( )
A. B. C.D.
3.设,则( )
A.B.0C.D.
4.为弘扬“五四”精神学校举行了一次演讲比赛,经过大数据分析,发现本次演讲比赛的成绩服从,据此估计比赛成绩不小于86的学生所占的百分比为( )
参考数据:,,
A.0.135%B.0.27%C.2.275%D.3.173%
5.函数的单调递减区间为( )
A. B. C. D.
6.已知a,b,c,d均为实数,则下列命题中正确的是( )
A.若,,则 B.若,则
C.若,则 D.若,,则
7.若函数在区间上有极值点,则实数a的取值范围是( )
A.B.C.D.
8.已知是定义在R上的奇函数,对任意两个不相等的正数,都有,记,,,则下列大小关系正确的是( )
A. B. C. D.
二、多项选择题(本大题共3小题,每小题6分,共18分。在每小题给出的四个选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。)
9.已知随机变量的分布列为
若,则下列结论正确的是( )
A.B. C. D.
10.某计算机程序每运行一次都随机出现一个五位二进制数 (例如10 100),其中的各位数中,出现的概率为,出现的概率为,记,则当程序运行一次时,下列选项正确的是( )
A.服从二项分 B. C.的均值 D.的方差
11.位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的安排方法种数为( )
A.B.C.D.
三、填空题(本大题共3小题,每小题5分,共15分。)
12.已知函数在处的切线方程为,求 .
4
9
10
0.3
0.1
0.2
13.的展开式中含项的系数是 .
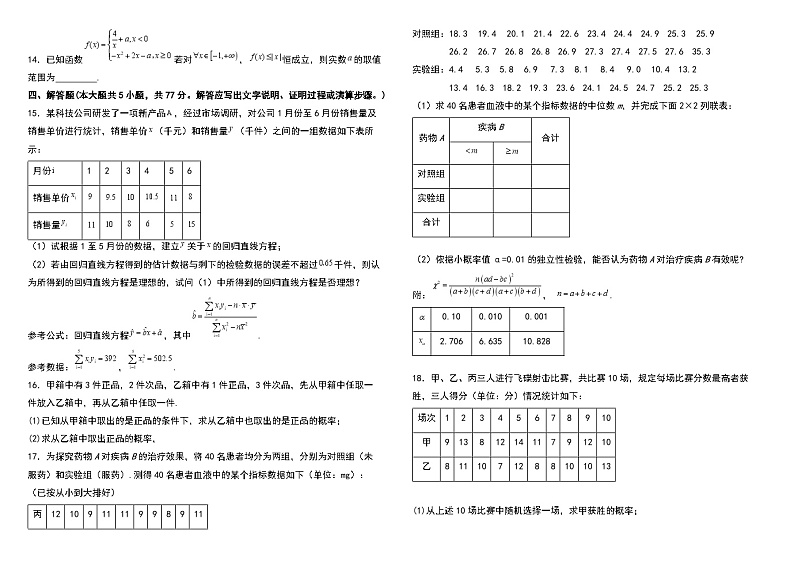
14.已知函数若对,恒成立,则实数的取值范围为 .
四、解答题(本大题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。)
15.某科技公司研发了一项新产品,经过市场调研,对公司1月份至6月份销售量及销售单价进行统计,销售单价(千元)和销售量(千件)之间的一组数据如下表所示:
(1)试根据1至5月份的数据,建立关于的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过千件,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
参考公式:回归直线方程,其中.
参考数据:,.
16.甲箱中有3件正品,2件次品,乙箱中有1件正品,3件次品,先从甲箱中任取一件放入乙箱中,再从乙箱中任取一件.
(1)已知从甲箱中取出的是正品的条件下,求从乙箱中也取出的是正品的概率;
(2)求从乙箱中取出正品的概率,
17.为探究药物A对疾病B的治疗效果,将40名患者均分为两组,分别为对照组(未服药)和实验组(服药).测得40名患者血液中的某个指标数据如下(单位:mg):(已按从小到大排好)
对照组:18.3 19.4 20.1 21.4 22.6 23.4 24.4 24.9 25.3 25.9
26.2 26.7 26.8 26.8 26.9 27.3 27.4 27.5 27.6 35.3
实验组:4.4 5.3 5.8 6.9 7.3 8.1 8.4 9.0 10.4 13.2
13.4 16.3 18.2 19.3 23.6 24.1 24.5 24.7 25.2 25.3
(1)求40名患者血液中的某个指标数据的中位数m,并完成下面2×2列联表:
(2)依据小概率值α=0.01的独立性检验,能否认为药物A对治疗疾病B有效呢?
附:, .
18.甲、乙、丙三人进行飞碟射击比赛,共比赛10场,规定每场比赛分数最高者获胜,三人得分(单位:分)情况统计如下:
月份
1
2
3
4
5
6
销售单价
销售量
药物A
疾病B
合计
对照组
实验组
合计
0.10
0.010
0.001
2.706
6.635
10.828
场次
1
2
3
4
5
6
7
8
9
10
甲
9
13
8
12
14
11
7
9
12
10
乙
8
11
10
7
12
8
8
10
10
13
(1)从上述10场比赛中随机选择一场,求甲获胜的概率;
(2)在上述10场比赛中,从甲得分不低于10分的场次中随机选择两场,设X表示乙得分大于丙得分的场数,求X的分布列和数学期望;
(3)假设每场比赛获胜者唯一,且各场相互独立,用上述10场比赛中每人获胜的频率估计其获胜的概率.甲、乙、丙三人接下来又将进行6场投篮比赛,设为甲获胜的场数,为乙获胜的场数,为丙获胜的场数,写出方差,,的大小关系(直接写出结果).
19.已知函数.
(1)当时,求曲线在点处的切线方程;
(2)讨论函数的单调性;
(3)若的有三个零点,求的取值范围.
哈师大青冈实验中学校2023-2024学年度期末考试
高二学年数学试题(答案)
一、单选题
1-4 DDAC. 5-8 B CCA.
二、多选题
9. BCD. 10.AC 11.BD.
三、填空题
12. 5 13. 13 14.
四、解答题
15. 【详解】(1)因为,,
所以,
得,
于是关于的回归直线方程为;
(2)当时,,
则,
丙
12
10
9
11
11
9
9
8
9
11
故可以认为所得到的回归直线方程是理想的
16.【详解】(1)设“从甲箱中取出正品”,“从乙箱中取出正品”,
先从甲箱中取出一件正品放入乙箱,此时乙箱中由2件正品,3件次品,
所求概率为
(2)设“从甲箱中取出正品”,“从乙箱中取出正品”,
易知,,,,故由全概率公式,
得
17.【详解】(1)依题意,这40个数据的中位数是将两组数据合在一起,从小到大排序后第20位与第21位数据的平均数,
由于原数据已经排好,所以只需要两组数据即可.
可得第20位数据为:23.4,第21位数据为:23.6,所以.
故列联表为:
(2)零假设:药物A对治疗疾病B无效,即药物A与治疗疾病B相互独立。
由题意:.
所以依据小概率值的独立性检验,我们没有充分证据推断不成立,故可认为药物A对治疗疾病B无效.
18.【详解】(1)解:根据三人投篮得分统计数据,在10场比赛中,甲共获胜5场,
设A表示“从10场比赛中随机选择一场,甲获胜”,则.
(2)解:根据三人投篮得分统计数据,在10场比赛中,甲得分不低于10分的场次有6场,其中乙得分大于丙得分的场次有4场,所以X的所有可能取值为,
可得,,,
所以变量的分布列为
所以,期望为.
(3)解:由题意,每场比赛甲获胜的概率为,乙获胜的概率为,丙获胜的概率为,
还需要进行6场比赛,而甲、乙、丙获胜的场数符合二项分布,
所以,,
,则.
19. 【详解】(1)当a=1时,,得,
,则,
所以切线方程为:,
即;
(2)由题,可得,
当时,当时,,此时在上单调递减,
当时,,此时在上单调递增,
当时,的解为,,
药物A
疾病B
合计
对照组
6
14
20
实验组
14
6
20
合计
20
20
40
X
0
1
2
P
①当,即时,恒成立,则在上单调递增;
②当,即时,
在区间,上,满足,在区间上,满足,
此时在,上单调递增;在上单调递减;
③当,即时,
在区间,上,满足,在区间上,满足,
即在,上单调递增;在上单调递减;
综上可知,当时,在上单调递减,在上单调递增;
当时,在,上单调递增,在上单调递减;
当时,在上单调递增;
当时,在,上单调递增,在上单调递减;
(3)①当时,在上单调递减,在上单调递增,
则最多两个零点,不合题意;
②当时,,知在上单调递增,在上单调递减,上单调递增;
可得在处取得极大值,在处取得极小值;
且时,,时,,要使得有三个零点,
则必有,即,此时可得a无解;
③当时,,则在上单调递增;则最多一个零点,不合题意;
④当时,,知在上单调递增,在上单调递减,在上单调递增,
可得在处取得极小值,在处取得极大值;
且时,,时,,要使得有三个零点,
则必有,即,解得且;
综上得a的取值范围是.
2023-2024学年黑龙江省绥化市哈尔滨师范大学青冈实验中学校高二上学期开学考试数学试题含答案: 这是一份2023-2024学年黑龙江省绥化市哈尔滨师范大学青冈实验中学校高二上学期开学考试数学试题含答案,共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年黑龙江省哈尔滨师范大学青冈实验中学校高一下学期期末考试数学试题(解析版): 这是一份2021-2022学年黑龙江省哈尔滨师范大学青冈实验中学校高一下学期期末考试数学试题(解析版),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年黑龙江省哈尔滨师范大学青冈实验中学校高二上学期期中考试数学试题(解析版): 这是一份2022-2023学年黑龙江省哈尔滨师范大学青冈实验中学校高二上学期期中考试数学试题(解析版),共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












