重庆市十八中学2023-2024学年数学八年级第一学期期末达标测试试题【含解析】

这是一份重庆市十八中学2023-2024学年数学八年级第一学期期末达标测试试题【含解析】，共18页。试卷主要包含了答题时请按要求用笔，下列二次根式中，可以与合并的是，的值是，如图，不是轴对称图形的是，下列命题中，真命题是等内容，欢迎下载使用。

注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题（每题4分，共48分）
1．如图，在的正方形格纸中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中是一个格点三角形.则图中与成轴对称的格点三角形有( )
A．个B．个C．个D．个
2．的绝对值是( )
A．B．C．D．
3．下列图形中，不是轴对称图形的是( )
A．B．C．D．
4．下列运算正确的是(
A．B．C．D．
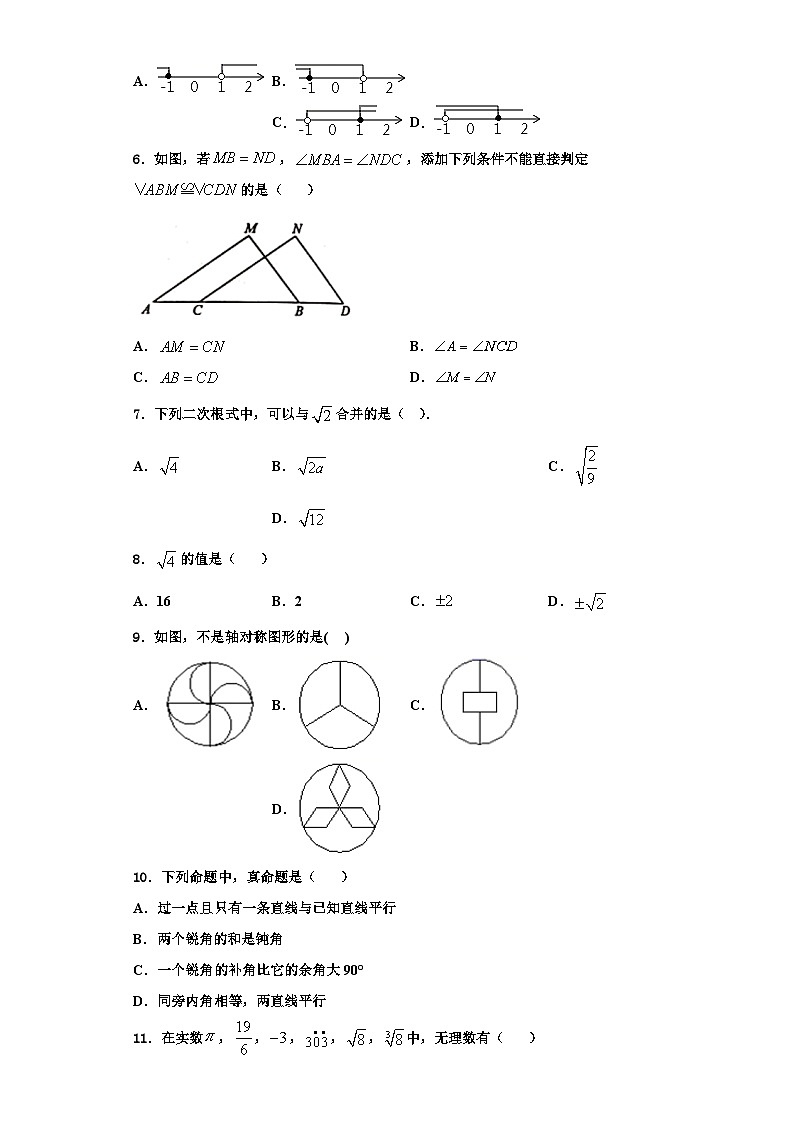
5．不等式组的解集在数轴上可表示为（ ）
A．B．C．D．
6．如图，若，，添加下列条件不能直接判定的是（ ）
A．B．
C．D．
7．下列二次根式中，可以与合并的是（ ）．
A． B． C． D．
8．的值是（ ）
A．16B．2C．D．
9．如图，不是轴对称图形的是( )
A．B．C．D．
10．下列命题中，真命题是（ ）
A．过一点且只有一条直线与已知直线平行
B．两个锐角的和是钝角
C．一个锐角的补角比它的余角大90°
D．同旁内角相等，两直线平行
11．在实数，，，，，中，无理数有（ ）
A．1个B．2个C．3个D．4个
12．计算：21+79=（ ）
A．282.6B．289C．354.4D．314
二、填空题（每题4分，共24分）
13．已知a、b、c为△ABC的三边，化简：|a+b﹣c|-|a﹣b﹣c|+|a﹣b+c|=______．
14．用四舍五入法将2.056精确到十分位的近似值为________．
15．如图，AB=DB，∠1=∠2，请你添加一个适当的条件，使△ABC≌△DBE，则需添加的条件是____（只要写一个条件）.
16．现有八个大小相同的矩形，可拼成如图1、2所示的图形，在拼图2时，中间留下了一个边长为2的小正方形，则每个小矩形的面积是_____．
17．将点P（-1，2）向左平移2个单位，再向上平移1个单位所得的对应点的坐标为_____．
18．将长为20cm、宽为8cm的长方形白纸，按如图所示的方法粘合起来，粘合部分的宽为3cm，设x张白纸粘合后的总长度为ycm，y与x之间的关系式为_______．
三、解答题（共78分）
19．（8分）学校为了丰富同学们的社团活动，开设了足球班．开学初在某商场购进A，B两种品牌的足球，购买A品牌足球花费了2400元，购买B品牌足球花费了1600元，且购买A品牌足球数量是购买B品牌足球数量的2倍，已知购买一个B品牌足球比购买一个A品牌足球多花20元．
(1)求所购买的A、B两种品牌足球的单价是多少元？
(2)为响应“足球进校园”的号召，决定再次购进A，B两种品牌足球共30个，恰逢商场对两种品牌足球的售价进行调整，A品牌足球售价比第一次购买时提高了10%，B品牌足球按第一次购买时售价的9折出售，如果这所中学此次购买A，B两种品牌足球的总费用不超过2000元，那么此次最多可购买多少个B品牌足球？
20．（8分）在中，，，点是线段上一动点（不与，重合）.
（1）如图1，当点为的中点，过点作交的延长线于点，求证：；
（1）连接，作，交于点.若时，如图1．
①______；
②求证：为等腰三角形；
（3）连接CD，∠CDE=30°，在点的运动过程中，的形状可以是等腰三角形吗？若可以，请求出的度数；若不可以，请说明理由．
21．（8分）在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（，5），（，3）．
⑴请在如图所示的网格平面内作出平面直角坐标系；
⑵请作出△ABC关于y轴对称的△A′B′C′；
⑶写出点B′的坐标．
22．（10分）电子商务的快速发展逐步改变了人们的生活方式，网购已悄然进入千家万户，张女士在某网店花220元买了1只茶壶和10只茶杯，已知茶壶的单价比茶杯的单价的4倍还多10元．
（1）求茶壶和茶杯的单价分别是多少元？
（2）新春将至，该网店决定推出优惠酬宾活动：买一只茶壶送一只茶杯，茶杯单价打八折．请你计算此时买1只茶壶和10只茶杯共需多少元？
23．（10分）先化简，再求值：
,其中
24．（10分）如图，直线L：与x轴、y轴分别交于A、B两点，在y轴上有一点，动点M从A点以每秒1个单位的速度沿x轴向左移动．
求A、B两点的坐标；
求的面积S与M的移动时间t之间的函数关系式；
当t为何值时≌，并求此时M点的坐标．
25．（12分）如图所示，△ABC在正方形网格中，若点A的坐标为(0，3)，按要求回答下列问题：
(1)在图中建立正确的平面直角坐标系；
(2)根据所建立的坐标系，写出点B和点C的坐标；
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
26．甲、乙两位同学5次数学成绩统计如表，他们的5次总成绩相同，小明根据他们的成绩绘制了尚不完整的统计图表，请同学们完成下列问题．
其中，甲的折线图为虚线、乙的折线图为实线．
甲、乙两人的数学成绩统计表
（1）a＝ ， ；
（2）请完成图中表示乙成绩变化情况的折线；
（3）S2甲＝260，乙成绩的方差是 ，可看出 的成绩比较稳定（填“甲”或“乙”）．从平均数和方差的角度分析， 将被选中．
参考答案
一、选择题（每题4分，共48分）
1、C
【分析】直接利用轴对称图形的性质分别得出符合题意的答案．
【详解】符合题意的三角形如图所示：
满足要求的图形有6个
故选：C
【点睛】
本题主要考查利用轴对称来设计轴对称图形，关键是要掌握轴对称的性质和轴对称图形的含义．
2、D
【解析】直接利用绝对值的定义分析得出答案．
【详解】解：-1的绝对值是：1．
故选：D．
【点睛】
此题主要考查了绝对值，正确把握绝对值的定义是解题关键．
3、C
【分析】根据轴对称图形的概念对各选项分析判断即可得解．
【详解】A．是轴对称图形，故本选项不合题意；
B．是轴对称图形，故本选项不合题意；
C．不是轴对称图形，故本选项符合题意；
D．是轴对称图形，故本选项不合题意．
故选：C．
【点睛】
此题考查轴对称图形的概念，解题关键在于寻找对称轴，图形两部分折叠后可重合．
4、C
【分析】分别根据合并同类项的法则、积的乘方运算法则、幂的乘方运算法则和同底数幂的除法法则逐项计算即可．
【详解】解：A、，所以本选项运算错误，不符合题意；
B、，所以本选项运算错误，不符合题意；
C、，所以本选项运算正确，符合题意；
D、，所以本选项运算错误，不符合题意．
故选：C．
【点睛】
本题考查的是合并同类项的法则和幂的运算性质，属于基础题型，熟练掌握幂的运算性质是解题关键．
5、D
【分析】先解不等式组可求得不等式组的解集是,再根据在数轴上表示不等式解集的方法进行表示.
【详解】解不等式组可求得:
不等式组的解集是,
故选D.
【点睛】
本题主要考查不等组的解集数轴表示,解决本题的关键是要熟练掌握正确表示不等式组解集的方法.
6、A
【分析】根据全等三角形的判定方法：SSS、SAS、ASA、AAS、HL，结合选项进行判定，然后选择不能判定全等的选项．
【详解】A、添加条件AM=CN，仅满足SSA，不能判定两个三角形全等；
B、添加条件AB=CD，可用SAS判定△ABM≌△CDN；
C、添加条件∠M=∠N，可用ASA判定△ABM≌△CDN；
D、添加条件∠A=∠NCD，可用AAS判定△ABM≌△CDN．
故选：A．
【点睛】
本题考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
7、C
【解析】分别将每一项化为最简二次根式，如果与是同类二次根式，即可合并.
【详解】解：A、，不能与合并，故A不符合题意；
B、不能与合并,故B不符合题意；
C、， 能与合并,故C符合题意；
D、， 不能与合并,故D不符合题意；
故答案为：C.
【点睛】
本题考查同类二次根式，解题的关键是熟练运用同类二次根式的概念．
8、B
【分析】根据算术平方根的定义求值即可．
【详解】=1．
故选：B．
【点睛】
本题考查算术平方根，属于基础题型．
9、A
【分析】根据轴对称图形的概念对各选项进行分析即可得出结论．
【详解】A．不是轴对称图形，故本选项正确；
B．是轴对称图形，故本选项错误；
C．是轴对称图形，故本选项错误；
D．是轴对称图形，故本选项错误．
故选：A．
【点睛】
本题考查了轴对称图形的识别，掌握轴对称图形的概念是解答本题的关键．
10、C
【分析】根据平行线的公理及判定、角的定义和补角和余角的定义可逐一判断．
【详解】解：A、过直线外一点有且只有一条直线与已知直线平行，是假命题；
B、两个锐角的和不一定是钝角，如20°+20°=40°，是假命题；
C、一个锐角的补角比它的余角大90°，是真命题；
D、同旁内角互补，两直线平行，是假命题；
故选：C．
【点睛】
本题主要考查平行线的公理及性质，掌握平行线的公理及判定、角的定义和补角和余角的定义是关键．
11、B
【分析】根据无理数的三种形式：①开方开不尽的数，②无线不循环小数，③含有π的数，找出无理数的个数即可．
【详解】解：，，
无理数有：π，共2个，
故选：B．
【点睛】
本题考查的是无理数的知识，掌握无理数的形式是解题的关键．
12、D
【分析】利用乘法分配律即可求解．
【详解】原式=
故选：D．
【点睛】
本题主要考查乘法运算律在实数运算中的应用，掌握乘法分配律是解题的关键．
二、填空题（每题4分，共24分）
13、
【解析】根据三角形的三边关系判断绝对值内式子的正负，然后利用绝对值的性质去掉绝对值，再去括号合并同类项即可．
【详解】解：∵a、b、c为△ABC的三边，
∴a+b＞c，a-b＜c，a+c＞b，
∴a+b-c＞0，a-b-c＜0，a-b+c＞0，
∴|a+b-c|-|a-b-c|+|a-b+c|
=(a+b-c)+(a-b- c)+(a-b+c)
=a+b-c+a-b- c+a-b+c
=3a-b-c．
故答案为：3a-b-c．
【点睛】
本题主要考查了三角形的三边关系定理和利用绝对值的性质进行化简，利用三角形的三边关系得出绝对值内式子的正负是解决此题的关键．
14、2.1
【分析】把百分位上的数字5进行四舍五入即可．
【详解】解：2.056精确到十分位的近似值为2.1；
故答案为：2.1．
【点睛】
本题考查了近似数和有效数字：近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．
15、BC＝BE（答案不唯一）
【分析】由∠1＝∠2利用角的和差可得∠DBE＝∠ABC，现在已知一个角和角的一边，再加一个边，运用SAS可得三角形全等.
【详解】解：∵∠1＝∠2
∴∠DBE＝∠ABC，
又∵AB＝DB，
∴添加BC＝BE，运用SAS即可证明△ABC≌△DBE．
故答案为：BC＝BE（答案不唯一）．
【点睛】
本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．根据已知条件选择适当的判定方法是解答本题的关键．
16、1．
【分析】设小矩形的长为x，宽为y，则由图1可得5y=3x；由图2可知2y-x=2.
【详解】解：设小矩形的长为x，宽为y，则可列出方程组，
，解得，
则小矩形的面积为6×10=1.
【点睛】
本题考查了二元一次方程组的应用.
17、 (-1，1)
【分析】直接利用平移中点的变化规律求解即可．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
【详解】原来点的横坐标是-1，纵坐标是2，向左平移2个单位，再向上平移1个单位得到新点的横坐标是-1−2＝-1，纵坐标为2+1＝1．
即对应点的坐标是(-1，1)．
故答案填：(-1，1)．
【点睛】
解题关键是要懂得左右平移点的纵坐标不变，而上下平移时点的横坐标不变，平移变换是中考的常考点，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
18、y=17x+1
【分析】由图可知，将x张这样的白纸粘合后的总长度=x张白纸的总长-(x-1)个粘合部分的宽，把相关数据代入化简即可得到所求关系式．
【详解】解：
由题意可得：y=20x-1(x-1)=17x+1，
即：y与x间的函数关系式为：y=17x+1．
故答案为：y=17x+1．
【点睛】
观察图形，结合题意得到：“白纸粘合后的总长度=x张白纸的总长-（x-1）个粘合部分的宽”是解答本题的关键．
三、解答题（共78分）
19、 (1)购买A种品牌足球的单价为60元/个，购买B种品牌足球的单价为80元/个；(2)此次最多可购买1个B品牌足球．
【分析】(1)设A，B两种足球单价分别为x，y.根据题中两个条件“购买B品牌足球花费了1600元，且购买A品牌足球数量是购买B品牌足球数量的2倍”列出和“购买一个B品牌足球比购买一个A品牌足球多花20元”列出.得到一个分式方程，最后要进行检验.
(2)设设购买y个B品牌足球，则购买(10﹣y)个A品牌足球.然后根据（1）中的单价分别计算出调整后的单价，A的单价为：60×(1+10%)，B单价为80×0.9 .最后再由A，B两种品牌足球的总费用不超过2000元建立一元一次不等式.
【详解】解：(1)设购买A种品牌足球的单价为x元/个，购买B种品牌足球的单价为y元/个，
根据题意得：
解得：
答：设购买A种品牌足球的单价为60元/个，购买B种品牌足球的单价为80元/个．
(2)设购买y个B品牌足球，则购买(10﹣y)个A品牌足球，
根据题意得：60×(1+10%)(10﹣y)+80×0.9y≤2000，
解得：．
∵y为整数，
∴y的最大值为1．
答：此次最多可购买1个B品牌足球．
【点睛】
本题考察了分式方程的实际应用与一元一次不等式的实际应用.在分式方程应用中，找准题干给出的条件列出等量关系式是解题关键，最重要的是结果要进行检验；而一元一次不等式的不等符号要判断正确，常见的容易出错的不等符号与文字之间的关系有：不超过（），不低于（），至多（），至少（）.
20、（1）证明见解析；（1）①110°；②证明见解析；（3）可以是等腰三角形，此时的度数为或．
【分析】（1）先证明△ACD与△BFD全等，即可得出结论；
（1）①先根据等边对等角及三角形的内角和求出∠B的度数，再由平行线的性质可得出∠ADE的度数，最后根据平角的定义可求出∠CDB的度数；②根据等腰三角形的性质以及平行线的性质可得出∠A=∠EDA，从而可得出结论；
（3）先假设△ECD可以是等腰三角形，再分以下三种情况：I.当时，；II.当时，；III.当时，，然后再根据等腰三角形的性质、三角形的内角和以及三角形外角的性质求解即可．
【详解】（1）证明：，是的中线，
．
，．
，
，
；
（1）①解：∵AC=BC，∠ACB=110°，
∴∠A=∠B=（180°-110°）÷1=30°，
又DE∥BC，
∴∠ADE=∠B=30°，
∴∠CDB=180°-∠ADE-∠EDC=110°，
故答案为：；
②证明：，．
，．
，
为等腰三角形．
（3）解：可以是等腰三角形，理由如下：
I.当时，，如图3，
．
，
．
II.当时，，如图4，
，
．
．
III.当时，．
∴，
，
此时，点与点重合，不合题意．
综上所述，可以是等腰三角形，此时的度数为或．
【点睛】
本题主要考查三角形的性质与判定，三角形全等的判定与性质，平行线的性质，三角形的内角和定理以及三角形外角的性质，掌握基本性质与判定定理是解题的关键．
21、⑴⑵如图，⑶B′(2,1)
【分析】（1）易得y轴在C的右边一个单位，x轴在C的下方3个单位；
（2）作出A，B，C三点关于y轴对称的三点，顺次连接即可；
（3）根据所在象限及距离坐标轴的距离可得相应坐标．
【详解】解：
（1）如图；
（2）如图；
（3）点B′的坐标为（2，1）．
22、（1）茶壶的单价为70元，茶杯的单价为15元．（2）178
【分析】（1）设茶壶的单价为x元，茶杯的单价为y元，根据题意列出方程组进行求解；
（2）根据题意实际只需要付一只茶壶和九只茶杯的钱．
【详解】解：（1）设茶壶的单价为x元，茶杯的单价为y元，
由题意得， ，
解得： ，
答：茶壶的单价为70元，茶杯的单价为15元；
（2）共需钱数为：70+0.8×15×9=178（元），
答：买1只茶壶和10只茶杯共需178元．
【点睛】
本题考查二元一次方程组的应用题，解题的关键是找到题目中的等量关系，列出方程组进行求解．
23、－2
【解析】试题分析：先化简,再将x的值代入计算即可.
试题解析：
原式＝
＝＋1
＝
当x＝时，原式＝＝－2
24、（1）A（0,4），B（0,2）；（2）；（3）当t＝2或1时，△COM≌△AOB，此时M（2，0）或（﹣2，0）．
【分析】（1）由直线L的函数解析式，令y＝0求A点坐标，x＝0求B点坐标；
（2）由面积公式S＝OM•OC求出S与t之间的函数关系式；
（3）若△COM≌△AOB，OM＝OB，则t时间内移动了AM，可算出t值，并得到M点坐标．
【详解】（1）∵y＝﹣x+2，
当x＝0时，y＝2；当y＝0时，x＝4，
则A、B两点的坐标分别为A（4，0）、B（0，2）；
（2）∵C（0，4），A（4，0）
∴OC＝OA＝4，
当0≤t≤4时，OM＝OA﹣AM＝4﹣t，S△OCM＝×4×（4﹣t）＝8﹣2t；
当t＞4时，OM＝AM﹣OA＝t﹣4，S△OCM＝×4×（t﹣4）＝2t﹣8；
∴的面积S与M的移动时间t之间的函数关系式为：
（3）∵OC＝OA，∠AOB＝∠COM＝90°，
∴只需OB＝OM，则△COM≌△AOB，
即OM＝2，
此时，若M在x轴的正半轴时，t＝2，
M在x轴的负半轴，则t＝1．
故当t＝2或1时，△COM≌△AOB，此时M（2，0）或（﹣2，0）．
【点睛】
本题考查了一次函数的性质和三角形的面积公式，以及全等三角形的判定与性质，理解全等三角形的判定定理是关键．
25、（1）作图见解析；（2）B（﹣3，﹣1），C（1，1）；（3）作图见解析．
【解析】试题分析：（1）根据点的坐标为（0，3），即可建立正确的平面直角坐标系；
（2）观察建立的直角坐标系即可得出答案；
（3）分别作点关于轴的对称点 连接则即为所求．
试题解析：
（1）所建立的平面直角坐标系如下所示
（2）点和点的坐标分别为：
（3）所作△如下图所示．
26、（1）a＝40，＝60；（2）见解析；（3）160，乙，乙；
【分析】（1）由折线统计图直接可得a的值，利用平均数的计算公式计算即可；
（2）根据乙的数据补全折线统计图，并注明图例，
（3）计算乙的方差，比较做出选择．
【详解】解：（1）根据折线统计图得，a＝40；＝（50+40+70+70+70）÷5＝60；
故答案为：40，60；
（2）甲、乙两人考试成绩折线图，如图所示：
（3）S2乙＝[（70﹣60）2+（50﹣60）2+（70﹣60）2+（40﹣60）2+（70﹣60）2]＝160，
∵S2甲＝260，
∴S2乙＜S2甲，
∴乙的成绩稳定，所以乙将被选中．
故答案为：160，乙、乙．
【点睛】
本题考查折线统计图和统计表、平均数和方差，解题的关键是掌握折线统计图和统计表的信息读取、平均数和方差的计算.
第1次
第2次
第3次
第4次
第5次
甲成绩
90
40
70
40
60
乙成绩
70
50
70
a
70