山东省德州市陵城区2023-2024学年七年级下学期期末考试数学试卷(含答案)

这是一份山东省德州市陵城区2023-2024学年七年级下学期期末考试数学试卷(含答案)，共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列各数：,,,0.333333,,1.21221222122221…(每两个1之间依次多一个2),3.14,中,无理数有( )
A.2个B.3个C.4个D.5个
2．已知,下列变形一定正确的是( )
A.B.C.D.
3．下列说法中正确的是( )
A.过一点有且只有一条直线垂直于己知直线
B.直线外一点到这条直线的垂线段,叫做这点到这条直线距离
C.经过直线外一点,有且仅有一条直线与已知直线平行
D.两条直线被第三条直线所截,回旁内角互补
4．把方程改写成含x的式子表示y的形式为( )
A.B.
C.D.
5．下面调查方式你认为比较合理的是( )
A.了解全校同学喜欢课程情况,对某班男同学进行调查.
B.了解某小区居民的防火意识,对你们班同学进行调查.
C.了解商场的平均日营业额,选在周末进行调查.
D.了解某校学生课外阅读的情况,从全校学生中随机抽取100名学生进行调查.
6．如图，点E在AC的延长线上，下列条件中能判断的是( )
A.B.
C.D.
7．已知点A的坐标为,线段AB平行于x轴且,则点B的坐标为( )
A.B.或C.D.或
8．若点在第二象限，则点在( )
A.第一象限B.第二象限C.第三象限D.第四象限
9．在数轴上表示不等式组的解集,正确的是( )
A.B.
C.D.
10．《孙子算经》是中国古代数学著作,其中记载：“今有木,不知长短、引绳度之,余绳四尺五寸,屈绳量之,不足一尺,木长几何？”译文：“用一根绳子去量一根木,绳子还剩余4.5尺,将绳子对折再量这根木,木还剩余1尺,问木长多少尺？”设绳子长x尺,木长y尺,可列方程组为( )
A.B.C.D.
11．如图,在四边形ABCD中,,,将四边形ABCD沿AB方向平移得到四边,BC与相交于点E,若,,,则阴影部分的面积为( )
A.B.13C.D.26
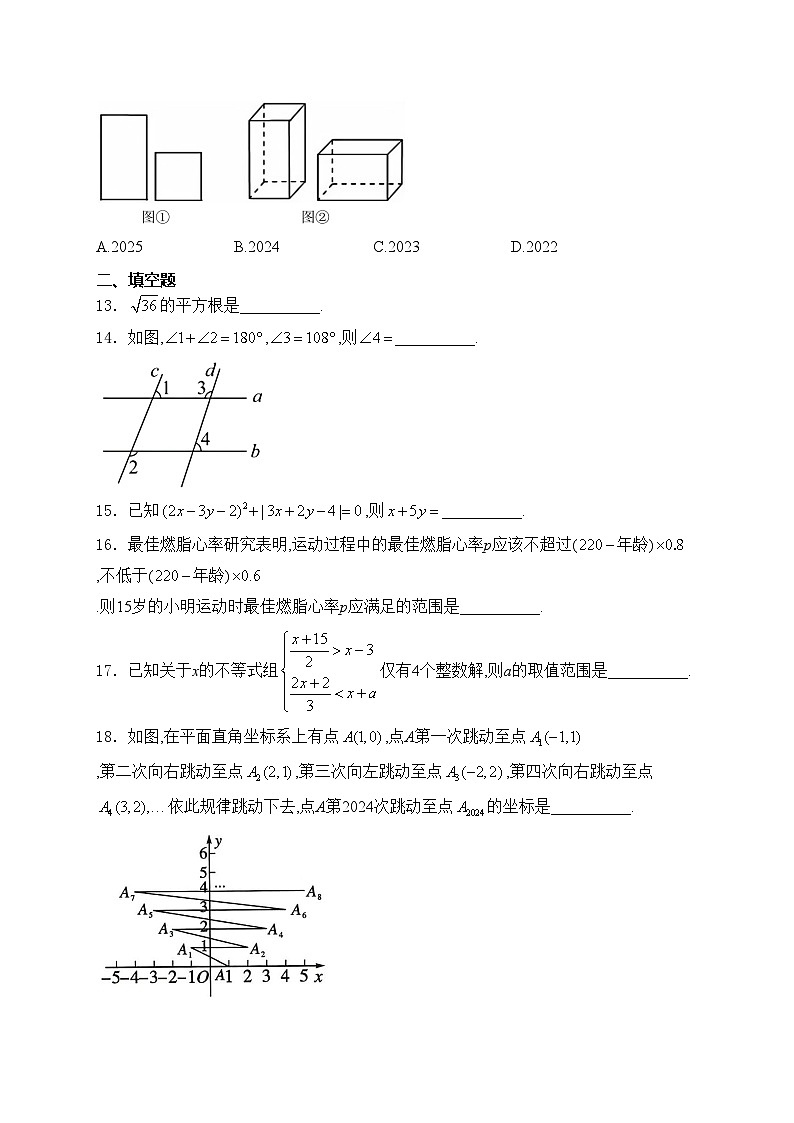
12．用如图①中的长方形和正方形纸板为侧面和底面,做成如图②的竖式和横式的两种无盖纸盒(图②中两个盒子朝上的一面不用纸板)现在仓库里有m张长方形纸板和n张正方形纸板,如果做两种纸盒若干个,恰好使库存的纸板用完,则的值有可能是( )
A.2025B.2024C.2023D.2022
二、填空题
13．的平方根是__________.
14．如图,,,则__________.
15．已知,则__________.
16．最佳燃脂心率研究表明,运动过程中的最佳燃脂心率p应该不超过(年龄),不低于(年龄).则15岁的小明运动时最佳燃脂心率p应满足的范围是__________.
17．已知关于x的不等式组仅有4个整数解,则a的取值范围是__________.
18．如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次向右跳动至点,第三次向左跳动至点,第四次向右跳动至点依此规律跳动下去,点A第2024次跳动至点的坐标是__________.
三、解答题
19．计算题.
(1)计算
(2)求不等式组的整数解并把解集表示在数轴上.
20．举世瞩目的中国共产党第二十次全国代表大会于2022年10月在北京成功召开.为弘扬党的二十大精神，某学校举办了“学习二十大，奋进新征程”的知识竞赛活动.赛后随机抽取了部分学生的成绩（满分：100分），分为A，B，C，D四组，绘制了如下不完整的统计图表：
学生成绩频数分布直方图
学生成绩扇形统计图
根据以上信息，解答以下问题：
（1）直接写出统计表中的________，________；
（2）学生成绩数据的中位数落在________组内；在学生成绩扇形统计图中，B组对应的扇形圆心角是________度；
（3）将上面的学生成绩频数分布直方图补充完整；
（4）若全校有1500名学生参加了这次竞赛，请估计成绩高于90分的学生人数.
21．如图,在平面直角坐标系中,的顶点分别为,,,经过平移得到,点A,B,C的对应点分别为,已知内任意一点,经平移后的对应点为.
(1)请描述如何平移得到,,；
(2)请画出平移后的,并写出,,三点的坐标；
(3)若,的面积为12,且点恰好在第一象限,求此时点P的坐标.
22．如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面EF,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,.
(1)求证：.
(2)若OE平分,,求扶手AB与靠背DM的夹角的度数.
23．定义：如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的【相伴方程】.
(1)在方程①,②,③中,不等式组的【相伴方程】是__________；(填序号)
(2)若不等式组的一个【相伴方程】的解是整数,则这个【相伴方程】是,求a的值；
(3)若方程,都是关于x的不等式组的【相伴方程】,求m的取值范围.
24．探索发现：(1)如图1,已知直线.若,,求的度数；
归纳总结：(2)根据(1)中的问题,写出图1中、、之间的数量关系为____________；
实践应用：(3)应用(2)中的结论解答下列问题：
①如图2,点A在B的北偏东的方向上,在C的北偏西的方向上,的度数为____________；
②如图3,已知直线,若,平分,平分,,求的度数.
25．某体有用品店准备购进甲、乙两种品牌跳绳,若购买甲种跳绳10根,乙种跳绳5根,需要100元,若购买甲种跳绳5根,乙种跳绳3根,需要55元.
(1)求购进甲,乙两种跳绳每根各需多少元？
(2)若该体育用品店刚好用了500元购进这两种跳绳,且销售每根甲种跳绳可获利润3元,销售每根乙种跳绳可获利润4元,考虑顾客需求,要求购进甲种跳绳的数量不少于乙种跳绳数量的3倍,且乙种跳绳数量不少于18根,那么该文具店共有哪几种购买方案？各种进货方案中,哪一种方案获利最大？最大利润是多少元？
(3)若体育用品店按(2)中利润最大方案去进货时,正值为促全民体育运动,两种跳绳每根各降价1元,体育用品店将省下的钱全部再次购买这两种跳绳,则再次购进有哪几种方案.
参考答案
1．答案：C
解析：是分数,0.333333,3.14是有限小数,是整数,它们不是无理数;,,1.212212212221…(每两个1之间依次多一个2),是无限不循环小数,它们是无理数,共4个;故选:C.
2．答案：D
解析：
A.,故此选项不符合题意;
B.不能推出,故此选项不符合题意;
C.当时,当时,当时,故此选项不符合题意;
D.一定成立,故此选项符合题意,
故选:D.
3．答案：C
解析：A、在同一平面内,过一点有且只有一条直线垂直于已知直线,故本选项错误,不符合题意;
B、从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线距离,故本选项错误,不符合题意;
C、过直线外一点有且只有一条直线与己知直线平行,故本选项正确,符合题意;
D、两条平行直线被第三条直线所截,同旁内角互补,故错误,不符合题意;
故选:C.
4．答案：B
解析：,移项得:,系数化为1得:,
故答案为:B.
5．答案：D
解析：A、了解全校同学喜欢课程情况,对某班男同学进行调查,不合理,不符合题意;
B、了解某小区居民的防火意识,对你们班同学进行调查,不合理,不符合题意;
C、了解商场的平均日营业额,选在周末进行调查,不合理,不符合题意;
D、了解某校学生课外阅读的情况,从全校学生中随机抽取100名学生进行调查,比较合理,符合题意;
故选:D.
6．答案：B
解析：A、，无法得到，，故此选项不符合；
B、，根据内错角相等，两直线平行可得：，故此选项符合；
C、，根据内错角相等，两直线平行可得：，故此选项不符合；
D、，根据同旁内角互补，两直线平行可得：，故此选项不符合；
故选：B.
7．答案：B
解析：由题知,因为线段AB平行于x轴,所以线段AB上所有点的纵坐标相等.又因为点A坐标为,且,所以点B的坐标为或.
故答案为:B.
8．答案：D
解析：点在第二象限，，，解得：，，则，，故点在第四象限.故选D.
9．答案：C
解析：由,得:,由,得:,不等式组的解集为,
故选:C.
10．答案：A
解析：设绳子长x尺,长木长y尺,
依题意,得:,
故选:A.
11．答案：B
解析：四边形ABCD沿AB方向平移得到四边形,
,,,
,
,
故选:B.
12．答案：A
解析：设可以制作x个竖式无盖纸盒,y个横式无盖纸盒,
根据题意得:,
①+②得:,
,y均为正整数,
是5的倍数,
可以是2025.
故选:A.
13．答案：
解析：因为,6的平方根是,所以的平方根是.
故正确答案为.
14．答案：
解析：因为所以所以.
15．答案：2
解析：,
,,
②-①,可得,
故答案为:2.
16．答案：
解析：根据题意,得,解得.
17．答案：
解析：①式两边同时乘2,得：,解得：；②式两边同时乘3,得；,解得：,此不等式组只有4个整数解,,解得:.
18．答案：
解析：由题知,
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;
点的坐标为;由此可见,点的坐标可表示为(n为正整数),
当,即时,
,
所以点的坐标为.
故答案为:.
19．答案：(1)
(2)1,2,数轴见解析
解析：(1)
解：原式
；
(2)
解不等式①,,得
解不等式②,,得,
把不等式①和不等式②的解集在数轴上表示出来：
∴不等式组的解集为,
∴不等式组的整数解为1,2.
20．答案：（1）40，80
（2），72
（3）见解析
（4）1050
解析：（1）由题意知，共调查（人），
（人），
（人），
故答案为：40，80；
（2）由题意知，中位数为第100，101位的数的平均数，
，，
中位数落在组内，
，
故答案为：，72；
（3）补全条形统计图如下：
（4）（人），
估计成绩高于90分的学生人数为1050人.
21．答案：(1)见解析
(2),,,图见解析
(3)
解析：(1)先向右平移3个单位长度,再向上平移2个单位长度得到.
或者先向上平移2个单位长度,再向右平移3个单位长度得到.(一种即可)
(2),,
平移后的如图所示：
(3)当时,
点P及其对应点的坐标分别为和
∵的面积为12,,,
∴
解得：
∴点P的坐标为.
22．答案：(1)证明见解析
(2)
解析：(1)证明：∵,,
∴,
∴；
(2)∵与底座都平行于地面,
∴,
∴,
∵,
∴,
∵平分,
∴,
∴,
∵,
∴.
23．答案：(1)①③
(2)
(3)
解析：(1),
,
方程①的解为：,
,
方程②的解为;
,
方程③的解为;
解不等式得,
解不等式得,
不等式组的解集为,
方程①③的解是不等式组的解,
不等式组
的【相伴方程】是①③;
故答案为:①③；
(2)解不等式得
解不等式得
∴不等式组的解集为
∴不等式组的整数解为
∵
∴
∵是不等式组的相伴方程
∴
∴
(3)∵∴
∵∴
∵方程,都是关于x的不等式组的相伴方程
解不等式组得
∴不等式组的解集为
∴
∴.
24．答案：(1)
(2)
(3)①
②
解析：(1)过P作
,
.
(2)；
(3)①；由(2)知
②平分,平分
,
由(2)中的结论有
.
25．答案：(1)购进甲种跳绳每根需要5元,购进乙种跳绳每根需要10元
(2)该商店有3种进货方案：方案①购进甲种跳绳60根,乙种跳绳20根；方案②购进甲种跳绳62根,乙种跳绳19根；方案③购进甲种跳绳64根,乙种跳绳18根；其中方案③获利最大,最大利润是264元
(3)共有2种再次购进方案：方案①：再次购进甲种跳绳16根,乙种跳绳2根；方案②再次购进甲种跳绳7根,乙种跳绳6根
解析：(1)设购进甲种跳绳每根需要x元,购进乙种跳绳每根需要y元,由题意得：
,解得：,
答：购进甲种跳绳每根需要5元,购进乙种跳绳每根需要10元.
(2)设购进乙种跳绳a根,则购进甲种跳绳根,根据题意得,
解得：,
∵a为正整数,
∴,
则
∵销售每根甲种跳绳可获利润3元,销售每根乙种跳绳可获利润4元,
方案①：利润为(元)；
方案②：利润为(元)；
方案③：利润为；
∵,
答：该商店有3种进货方案：方案①购进甲种跳绳60根,乙种跳绳20根；方案②购进甲种跳绳62根,乙种跳绳19根；方案③购进甲种跳绳64根,乙种跳绳18根；其中方案③获利最大,最大利润是264元.
(3)设再次购进甲种跳绳m根,乙种跳绳n根.
根据题意可列方程：
∵m,n都是正整数
∴得或
答：共有2种再次购进方案：方案①：再次购进甲种跳绳16根,乙种跳绳2根；方案②再次购进甲种跳绳7根,乙种跳绳6根.
组别
成绩（：分）
频数
A
20
B
m
C
60
D
n