辽宁省沈阳134中学2023-2024学年数学八年级第一学期期末预测试题【含解析】

这是一份辽宁省沈阳134中学2023-2024学年数学八年级第一学期期末预测试题【含解析】，共15页。试卷主要包含了化简－5a·，结果正确的是，已知，在平面直角坐标系中，点在，若分式的值为0，则的值为等内容，欢迎下载使用。

注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题（每题4分，共48分）
1．已知的外角中，若，则等于（ ）
A．50°B．55°C．60°D．65°
2．一汽艇保持发动机的功率不变，它在相距30千米的两码头之间流动的河水中往返一次（其中汽艇的速度大于河水流动的速度）所用的时间是t1，它在平静的河水中行驶60千米所用的时间是t2，则t1与t2的关系是（ ）
A．t1＞t2B．t1 ＜t2C．t1 =t2D．以上均有可能
3．已知点A（m+2，﹣3），B（﹣2，n﹣4）关于y轴对称，则m﹣n的值为（ ）
A．4B．﹣1C．1D．0
4．平面直角坐标系中，点P（-3,4）关于轴对称的点的坐标为（ ）
A．（3,4）B．（-3,-4）C．（-3,4）D．（3,-4）
5．化简－5a·(2a2－ab)，结果正确的是( )
A．－10a3－5abB．－10a3－5a2bC．－10a2＋5a2bD．－10a3＋5a2b
6．已知：点A（m﹣1，3）与点B（2，n﹣1）关于x轴对称，则（m+n）2019的值为（ ）
A．0B．1C．﹣1D．32019
7．如图，从标有数字1,2,3.4的四个小正方形中拿走一个，成为一个轴对称图形，则应该拿走的小正方形的标号是（ ）
A．1B．2C．3D．4
8．在平面直角坐标系中，点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
9．若分式的值为0，则的值为（ ）
A．1B．-1C．1或-1D．0
10．如图，AD是等边三角形ABC的中线，AE=AD，则∠EDC=（ ）度．
A．30B．20C．25D．15
11．已知，则（ ）
A．4033B．4035C．4037D．4039
12．如图，有A、B、C三个居民小区，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）
A．∠A、∠B两内角的平分线的交点处
B．AC、AB两边高线的交点处
C．AC、AB两边中线的交点处
D．AC、AB两边垂直平分线的交点处
二、填空题（每题4分，共24分）
13．若直线与直线的交点在轴上，则_______．
14．方程的根是______.
15． 在实数－5，－，0，π，中，最大的数是________．
16．长、宽分别为、的长方形，它的周长为16，面积为10，则的值为____.
17．已知一个正多边形的内角和为1080°，则它的一个外角的度数为_______度．
18．分解因式：_______．
三、解答题（共78分）
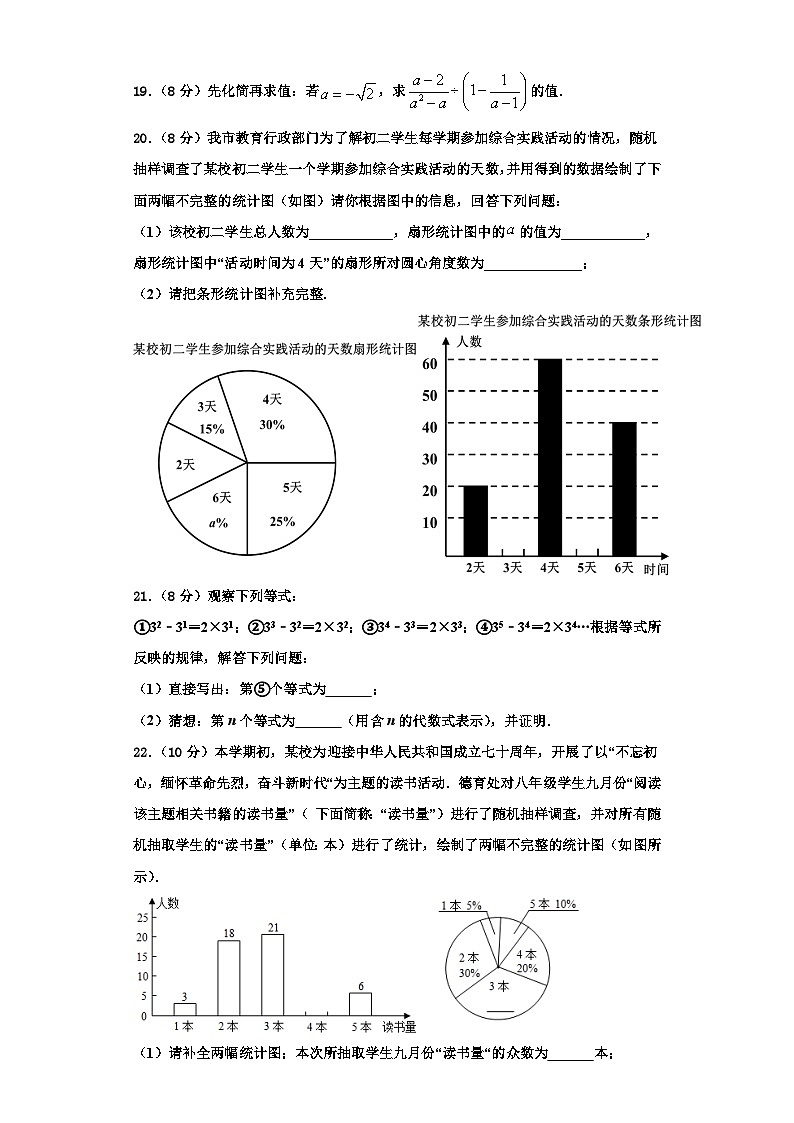
19．（8分）先化简再求值：若，求的值．
20．（8分）我市教育行政部门为了解初二学生每学期参加综合实践活动的情况，随机抽样调查了某校初二学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）请你根据图中的信息，回答下列问题：
（1）该校初二学生总人数为____________，扇形统计图中的的值为____________，扇形统计图中“活动时间为4天”的扇形所对圆心角度数为______________；
（2）请把条形统计图补充完整.
21．（8分）观察下列等式：
①32﹣31＝2×31；②33﹣32＝2×32；③34﹣33＝2×33；④35﹣34＝2×34…根据等式所反映的规律，解答下列问题：
（1）直接写出：第⑤个等式为 ；
（2）猜想：第n个等式为 （用含n的代数式表示），并证明．
22．（10分）本学期初，某校为迎接中华人民共和国成立七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代“为主题的读书活动．德育处对八年级学生九月份“阅读该主题相关书籍的读书量”（ 下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，绘制了两幅不完整的统计图（如图所示）．
（1）请补全两幅统计图；本次所抽取学生九月份“读书量“的众数为 本；
（2）求本次所抽取学生九月份“读书量”的平均数；
（3）已知该校八年级有500名学生，请你估计该校八年级学生中，九月份“读书量“为5本的学生人数．
23．（10分）如图，，，求证：.
24．（10分）某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨1.9元收费．如果超过20吨，未超过的部分按每吨1.9元收费，超过的部分按每吨2.8元收费．设某户每月用水量为x吨，应收水费为y元．
（1）分别写出每月用水量未超过20吨和超过20吨，y与x间的函数关系式．
（2）若该城市某户5月份水费平均为每吨2.2元，求该户5月份用水多少吨．
25．（12分）如图，已知在和中，交于点，
求证:；
当时，求的度数．
26．解分式方程
（1）
（2）
参考答案
一、选择题（每题4分，共48分）
1、B
【分析】三角形的一个外角等于和它不相邻的两个内角的和．根据三角形的外角的性质计算即可．
【详解】解：∵∠ACD是△ABC的一个外角，
∴∠ACD=∠B+∠A，
∵∠B=70°，
∴∠A=∠ACD-∠B=125°-70°=55°，
故选：B．
【点睛】
本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
2、A
【分析】设汽艇在静水中的速度为a千米/小时，水速为b千米/小时，根据题意列出算式，然后再比较大小即可．
【详解】汽艇在静水中所用时间t1．
汽艇在河水中所用时间 t1．
∵ t1－t1=0，∴，∴t1＞t1．
故选A．
【点睛】
本题考查了分式的减法，根据题意列出汽艇在静水中和河水中所用时间的代数式是解题的关键．
3、B
【分析】直接利用关于y轴对称的点的性质得出m，n的值，进而得出答案．
【详解】∵点A（m+2，﹣3），B（﹣2，n－4）关于y轴对称，
∴m＋2＝2，n－4＝﹣3
解得：m＝0，n＝1
则m－n＝﹣1
故选：B
【点睛】
本题考查关于y轴对称的点的坐标特征：关于y轴对称的两点，纵坐标相同，横坐标互为相反数．掌握关于y轴对称的点的坐标特征是解题的关键．
4、B
【分析】根据点关于坐标轴对称的特点，即可得到答案．
【详解】解：∵关于x轴对称，则横坐标不变，纵坐标变为相反数，
∴点P（）关于x轴对称的点坐标为：（），
故选：B．
【点睛】
本题考查了轴对称的性质，解题的关键是熟练掌握点关于坐标轴对称的特点，从而进行解题．
5、D
【解析】试题分析：根据单项式乘以多项式的计算法则进行计算，原式=，故选D．
6、B
【分析】根据关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数可得m、n的值，进而可得答案．
【详解】解：∵点A（m﹣1，3）与点B（2，n﹣1）关于x轴对称，
∴m﹣1＝2，n﹣1＝﹣3，
∴m＝3，n＝﹣2，
∵（m+n）2019＝1，
故选：B．
【点睛】
本题考查坐标对称点的特性，熟记知识点是解题关键.
7、B
【分析】根据轴对称图形的概念，逐一判断选项，即可得到答案.
【详解】∵拿走数字1的小正方形，不是轴对称图形，
∴A错误；
∵拿走数字2的小正方形，可得轴对称图形，
∴B正确；
∵拿走数字3的小正方形，不是轴对称图形，
∴C错误；
∵拿走数字4的小正方形，不是轴对称图形，
∴D错误；
故选B.
【点睛】
本题主要考查轴对称图形的概念，掌握轴对称图形的概念，是解题的关键.
8、B
【分析】根据各象限内点的坐标特征解答．第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
【详解】点在第二象限.
故选B.
【点睛】
此题考查象限及点的坐标的有关性质，解题关键在于掌握其特征.
9、A
【解析】根据分式的概念，分式有意义要求分母不为零，所以分式值为零，即分子为零即可．
【详解】 ，
，
，
故选：A．
【点睛】
考查分式的定义，理解定义以及有意义的条件是解题的关键．
10、D
【详解】∵△ABC是等边三角形，
∴AB=AC,∠BAC=∠C=60°，
∵AD是△ABC的中线，
∴∠DAC=∠BAC=30°，AD⊥BC，
∴∠ADC=90°，
∵AE=AD，
∴∠ADE=∠AED= ==75°，
∴∠EDC=∠ADC−∠ADE=90°−75°=15°.
故选D.
【点睛】
此题考查了等边三角形的性质、等腰三角形的性质及三角形的内角和定理的应用.解题的关键是注意三线合一与等边对等角的性质的应用，注意数形结合思想的应用．
11、C
【分析】根据得出a的值，再对2a+3进行运算化简即可．
【详解】解：∵
∴
∴

∴
故答案为：C．
【点睛】
本题考查了代数式的运算，解题的关键是对2a+3进行化简．
12、D
【分析】根据线段垂直平分线的性质即可得出答案．
【详解】解：根据线段垂直平分线上的点到线段两个端点的距离相等，超市应建在AC、AB两边垂直平分线的交点处，
故选：D．
【点睛】
本题考查了线段垂直平分线性质，注意：线段垂直平分线上的点到线段两个端点的距离相等．
二、填空题（每题4分，共24分）
13、1
【分析】先求出直线与y轴的交点坐标为（0，1），然后根据两直线相交的问题，把（0，1）代入即可求出m的值．
【详解】解：当x=0时，=1，则直线与y轴的交点坐标为（0，1），
把（0，1）代入得m=1，
故答案为：1．
【点睛】
本题考查了两条直线相交或平行的问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解；若两条直线是平行的关系，那么他们的自变量系数相同，即k值相同．
14、，
【分析】直接开方求解即可.
【详解】解：∵
∴
∴，
故答案为：，.
【点睛】
本题主要考查了解一元二次方程，熟练掌握解一元二次方程的几种方法是解题的关键.
15、π
【解析】根据正数大于0，0大于负数，正数大于负数，比较即可．
【详解】根据实数比较大小的方法，可得π＞＞0＞−＞−5，
故实数－5，－，0，π，中最大的数是π．
故答案为π．
【点睛】
此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．
16、80
【解析】∵长、宽分别为a、b的矩形，它的周长为16，面积为10，
∴a+b=16÷2=8，ab=10，
∴a²b+ab²=ab(a+b)=10×8=80，
故答案为80.
17、45
【分析】利用n边形内角和公式求出n的值，再结合多边形的外角和度数为即可求出一个外角的度数.
【详解】解：设这个正多边形为正n边形，根据题意可得
解得
所以该正多边形的 一个外角的度数为45度.
故答案为：45.
【点睛】
本题考查了多边形内角和与外角和，灵活利用多边形的内角和与外角和公式是解题的关键.
18、
【分析】根据提公因式法即可解答．
【详解】解：
故答案为：．
【点睛】
本题考查了分解因式，解题的关键是掌握提公因式法，准确提出公因式．
三、解答题（共78分）
19、，
【分析】先把分式化简后，再把的值代入求出分式的值．
【详解】解：
，
把代入得，原式.
【点睛】
本题考查了分式的化简求值，熟练分解因式是解题的关键．
20、（1）200人，20，108°；（2）见解析
【分析】（1）根据图中4天的人数和百分比算出初二的总人数，再根据6天的人数算出对应的百分比即可得a，根据4天所占百分比乘360°即可得对应圆心角度数.
（2）分别根据3天和5天的百分比，乘上总人数，得到对应的人数，即可补全图形.
【详解】解：（1）由图可知：4天的人数为60人，所占总人数的30%，
则初二总人数为：60÷30%=200（人），
∵6天对应的人数为40，
∴6天对应百分比为：40÷200×100%=20%，
即a=20，
“活动时间为4天”对应的圆心角为：360°×30%=108°；
（2）“3天”对应的人数为：200×15%=30（人），
“5天”对应的人数为：200×25%=50（人），
补全图形如下：
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
21、（1）36﹣35＝2×35；（2）3n+1﹣3n＝2×3n．
【分析】由①32﹣31＝2×31；②33﹣32＝2×32；③34﹣33＝2×33；④35﹣34＝2×34…得出第⑤个等式，以及第n个等式的底数不变，指数依次分别是n+1、n、n．
【详解】解：（1）由①32﹣31＝2×31；②33﹣32＝2×32；③34﹣33＝2×33；④35﹣34＝2×34…得出第⑤个等式36﹣35＝2×35；
故答案为36﹣35＝2×35；
（2）由①32﹣31＝2×31；②33﹣32＝2×32；③34﹣33＝2×33；④35﹣34＝2×34…得出第n个等式的底数不变，指数依次分别是n+1、n、n，
即3n+1﹣3n＝2×3n．
证明：左边＝3n+1﹣3n＝3×3n﹣3n＝3n×（3﹣1）＝2×3n＝右边，所以结论得证．
故答案为3n+1﹣3n＝2×3n．
【点睛】
此题考查数字的变化规律，找出数字之间的运算规律，得出规律，利用规律，解决问题．
22、（1）3本；（2）3；（3）该校八年级学生中，九月份“读书量“为5本的学生人数有50人
【分析】（1）根据统计图可知众数为3；
（2）利用读书总量除以学生总数即得平均数；
（3）根据百分比进行计算即可；
【详解】解：（1）读4本的人数有：×20%＝12（人），
读3本的人数所占的百分比是1﹣5%﹣10%﹣30%﹣20%＝35%，
补图如下：
根据统计图可知众数为3本，
故答案为：3本；
（2）本次所抽取学生九月份“读书量”的平均数是：
＝3（本）；
（3）根据题意得：
500×10%＝50（本），
答：该校八年级学生中，九月份“读书量“为5本的学生人数有50人．
【点睛】
本题是条形统计图和扇形统计图的综合运用．读懂统计图，解题关键是从不同的统计图中得到必要的信息．
23、证明见解析.
【分析】由两直线平行内错角相等可得，，由公共边，可以证明，由全等三角形对应边相等即可证明.
【详解】，，
，，
在和中
，
.
【点睛】
利用两直线平行的性质，可以得出两直线平行内错角相等，由全等三角形的判定定理可以证明，三角形全等可得对应边相等即可.
24、（1）当x≤20时，y=1.9x；当x＞20时，y=2.1x﹣11；（2）4吨．
【分析】（1）未超过20吨时，水费y=1.9×相应吨数；超过20吨时，水费y=1.9×20+超过20吨的吨数×2.1．
（2）该户的水费超过了20吨，关系式为：1.9×20+超过20吨的吨数×2.1=用水吨数×2.2．
【详解】解：（1）当x≤20时，y=1.9x；
当x＞20时，y=1.9×20+（x﹣20）×2.1=2.1x﹣11．
（2）∵5月份水费平均为每吨2.2元，用水量如果未超过20吨，按每吨1.9元收费．
∴用水量超过了20吨．
∴由y=2.1x﹣11，得2.1x﹣11=2.2x，
解得x=4．
答：该户5月份用水4吨．
【点睛】
本题考查一次函数的应用．
25、（1）证明见解析；（2）∠BOC=70°．
【分析】（1）求出∠BAE=∠CAF，根据SAS推出△BAE≌△CAF，推出BE=CF即可；
（2）求出∠EBA+∠BDA=110°，求出∠ACF+∠CDO=110°，即可得出答案；
【详解】（1）∵∠CAB=∠EAF，
∴∠CAB+∠CAE=∠EAF+∠CAE，
∴∠BAE=∠CAF，
在△BAE和△CAF中，
，
∴△BAE≌△CAF（SAS），
∴BE=CF；
（2）∵△BAE≌△CAF，
∴∠EBA=∠FCA，
∵∠CAB=70°，
∴∠EBA+∠BDA=180°-70°=110°，
∵∠BDA=∠CDE，∠EBA=∠FCA，
∴∠ACF+∠CDE=110°，
∴∠BOC=180°-（∠ACF+∠CDE）=180°-110°=70°．
【点睛】
本题考查了全等三角形的判定与性质，三角形内角和定理的应用，准确识图，熟练掌握和灵活运用相关知识是解题的关键．
26、（1）x；（2）无解．
【分析】（1）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
【详解】（1）
去分母得：x﹣1=﹣1﹣2(x-2)，
去括号得：x﹣1=﹣1﹣2x+4，
移项合并得：3x=4，
解得：x，
经检验x是分式方程的解；
（2）去分母得：
去括号得：x2+2x﹣x2﹣x+2=3，
移项合并得：x=1，
经检验x=1是增根，分式方程无解．
【点睛】
此题主要考查分式方程的求解，解题的关键是熟知分式方程的解法．