辽宁省辽河油田欢喜岭第二初级中学2023-2024学年数学八上期末学业质量监测模拟试题【含解析】

这是一份辽宁省辽河油田欢喜岭第二初级中学2023-2024学年数学八上期末学业质量监测模拟试题【含解析】，共18页。试卷主要包含了考生必须保证答题卡的整洁，下列运算中，结果是a5的是，一次函数的图象经过等内容，欢迎下载使用。

考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．小亮家1月至10月的用电量统计如图所示，这组数据的众数和中位数分别是（ ）
A．30和 20B．30和25C．30和22.5D．30和17.5
2．如图，高速公路上有两点相距10km，为两村庄，已知于，于,现要在上建一个服务站，使得两村庄到站的距离相等，则的长是（ ）km．
A．4B．5C．6D．
3．如图，，要说明，需添加的条件不能是（ ）
A．B．C．D．
4．下列运算中，结果是a5的是（ ）
A．a2 • a3B．a10 a2C．(a2)3D．( - a)5
5．正比例函数y＝kx(k≠0)的图象经过第二、四象限，则一次函数y＝x＋k的图象大致是( )
A．B．C．D．
6．下列给出的三条线段的长，能组成直角三角形的是（ ）
A．B．C．D．
7．如图，在平面直角坐标系中，已知点A（﹣2，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的正半轴于点C，则点C的横坐标介于（ ）
A．0和1之间B．1和2之间C．2和3之间D．3和4之间
8．一次函数的图象经过（ ）
A．第、、象限B．第、、象限C．第、、象限D．第、、象限
9．若不等式组，只有三个正整数解，则a的取值范围为( )
A．B．C．D．
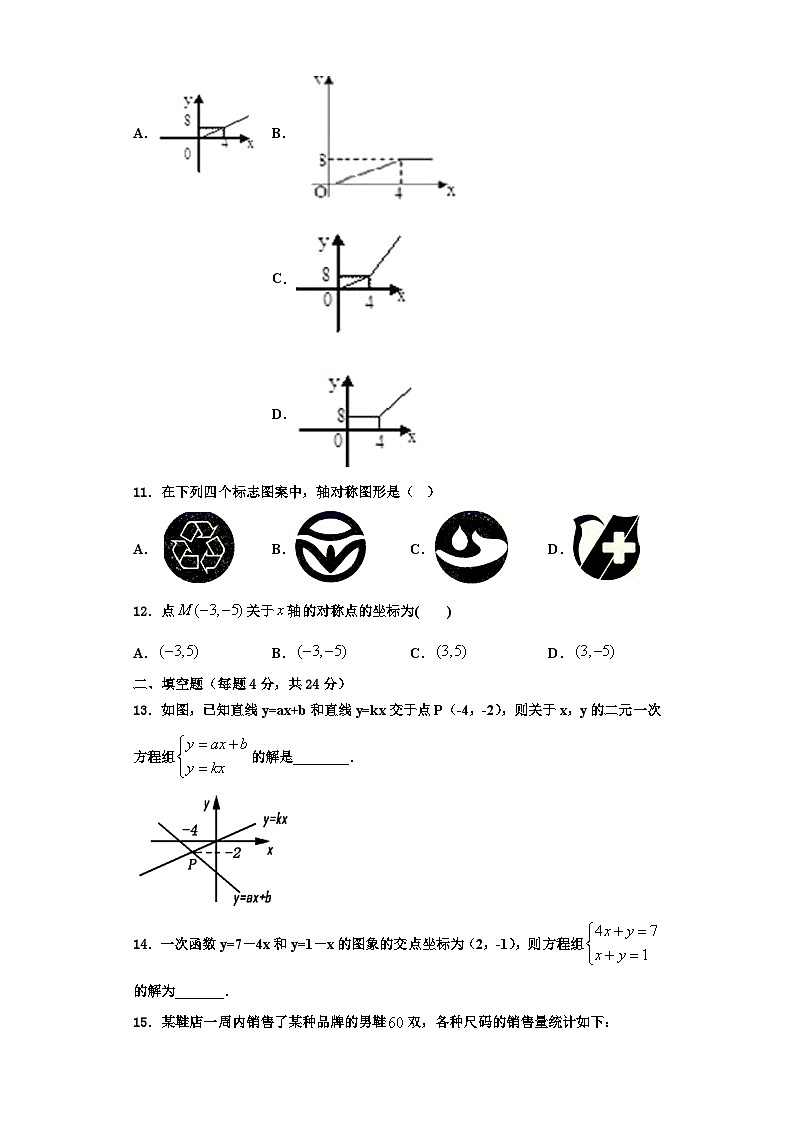
10．2014年6月3日中央新闻报道，为鼓励居民节约用水，北京市将出台新的居民用水收费标准：若每月每户居民用水不超过4m3，则按每立方米2元计算；若每月每户居民用水超过4m3，则超过部分按每立方米4.5元计算（不超过部分仍按每立方米2元计算）．现假设该市某户居民用水x m3，水费为y元，则y与x的函数关系式用图象表示正确的是（ ）
A．B．C．D．
11．在下列四个标志图案中，轴对称图形是（ ）
A． B．C．D．
12．点关于轴的对称点的坐标为( )
A．B．C．D．
二、填空题（每题4分，共24分）
13．如图，已知直线y=ax+b和直线y=kx交于点P（-4，-2），则关于x，y的二元一次方程组的解是________．

14．一次函数y=7－4x和y=1－x的图象的交点坐标为（2，-1），则方程组的解为_______．
15．某鞋店一周内销售了某种品牌的男鞋双，各种尺码的销售量统计如下：
由此你能给这家鞋店提供的进货建议是________________________.
16．《孙子算经》是中国古代重要的数学著作，现在的传本共三卷，卷上叙述算筹记数的纵横相间制度和筹算乘除法；卷中举例说明筹算分数算法和筹算开平方法；卷下记录算题，不但提供了答案，而且还给出了解法，其中记载：“今有木、不知长短，引绳度之，余绳四尺五寸，屈绳量之，不足一尺，木长几何？”译文:“用一根绳子量一根长木，绳子还剩余尺，将绳子对折再量长木，长木还到余尺，问木长多少尺？”设绳长尺，木长尺.可列方程组为__________．
17．在中，，为直线上一点，为直线上一点，，设，．
（1）如图1，若点在线段上，点在线段上，则，之间关系式为__________．
（2）如图2，若点在线段上，点在延长线上，则，之间关系式为__________．
18．如图，中，于D，要使，若根据“”判定，还需要加条件__________
三、解答题（共78分）
19．（8分）化简
（1）
（2）
20．（8分）如图，∠ADB＝∠ADC，∠B＝∠C．
（1）求证：AB＝AC；
（2）连接BC，求证：AD⊥BC．
21．（8分）（2017广东省）如图，在△ABC中，∠A＞∠B．
（1）作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，连接AE，若∠B=50°，求∠AEC的度数．
22．（10分）如图1，在Rt△ABC中，∠C＝90°，AC＝BC，点D，E分别在边AC，BC上，CD＝CE，连接AE，点F，H，G分别为DE，AE，AB的中点连接FH，HG
（1）观察猜想图1中，线段FH与GH的数量关系是 ，位置关系是
（2）探究证明：把△CDE绕点C顺时针方向旋转到图2的位置，连接AD，AE，BE判断△FHG的形状，并说明理由
（3）拓展延伸：把△CDE绕点C在平面内自由旋转，若CD＝4，AC＝8，请直接写出△FHG面积的最大值
23．（10分）先化简（﹣）÷，再从a≤2的非负整数解中选一个适合的整数代入求值．
24．（10分）如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．
⑴若∠AFD=155°，求∠EDF的度数；
⑵若点F是AC的中点，求证：∠CFD=∠B．
25．（12分）某商店经销一种泰山旅游纪念品，4月份的营业额为2000元，为扩大销售量，5月份该商店对这种纪念品打9折销售，结果销售量增加20件，营业额增加700元．
（1）求该种纪念品4月份的销售价格；
（2）若4月份销售这种纪念品获利800元，5月份销售这种纪念品获利多少元？
26．王阿姨到超市购买大米,元旦前按原价购买,用了元,元旦后,这种大米折出售,她用元又买了一些,两次一共购买了,这种大米的原价是多少?
参考答案
一、选择题（每题4分，共48分）
1、C
【分析】将折线统计图中的数据从小到大重新排列后，根据中位数和众数的定义求解可得．
【详解】将这10个数据从小到大重新排列为：10、15、15、20、20、25、25、30、30、30，
所以该组数据的众数为30、中位数为=22.5，
故选C．
【点睛】
此题考查了众数与中位数，众数是一组数据中出现次数最多的数；中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
2、A
【分析】根据题意设出EB的长为，再由勾股定理列出方程求解即可．
【详解】设EB=x，则AE=10-x，
由勾股定理得：
在Rt△ADE中，
，
在Rt△BCE中，
，
由题意可知：DE=CE，
所以：=，
解得：(km)．
所以，EB的长为4km．
故选：A．
【点睛】
本题主要考查的是勾股定理的运用，主要是运用勾股定理将两个直角三角形的斜边表示出来，运用方程思想求解．
3、D
【分析】根据全等三角形的判定定理判断即可．
【详解】A、在△ABC和△DCB中
∴△ABC≌△DCB，故本选项正确；
B、在△ABC和△DCB中
∴△ABC≌△DCB，故本选项正确；
C、∵
∴
在△ABC和△DCB中
∴△ABC≌△DCB，故本选项正确；
D、根据两边和其中一边的对角不能判断两三角形全等；故本选项错误；
故选：D．
【点睛】
本题主要考查对全等三角形的判定的理解和掌握，能熟练地根据等腰三角形的性质及全等三角形的判定定理进行证明是解此题的关键．
4、A
【分析】根据同底数幂的乘法法则、同底数幂的除法法则、幂的乘方、及乘方的意义逐项计算即可．
【详解】A. a2 • a3=a5，故正确；
B. a10 a2=a8，故不正确；
C. (a2)3=a6，故不正确；
D. ( - a)5=-a5，故不正确；
故选A．
【点睛】
本题考查了幂的运算，熟练掌握幂的运算法则是解答本题的关键．同底数的幂相乘，底数不变，指数相加；同底数幂相除，底数不变指数相减；幂的乘方，底数不变，指数相乘．
5、B
【解析】∵正比例函数y＝kx(k≠0)的图像经过第二、四象限，
∴k＜0，
∴一次函数y＝x＋k的图像与y轴交于负半轴，且经过第一、三象限．
故选B.
6、D
【分析】三角形三边满足两个较小边的平方和等于较大边的平方，这个三角形就是直角三角形．
【详解】A、因为12+22≠32，所以三条线段不能组成直角三角形；
B、因为22+32≠42，所以三条线段不能组成直角三角形；
C、因为52+72≠92，所以三条线段不能组成直角三角形；
D、因为32+42=52，所以三条线段能组成直角三角形．
故选：D．
【点睛】
本题考查勾股定理的逆定理，关键知道两个较小边的平方和等于较大边的平方，这个三角形就是直角三角形．
7、B
【分析】先根据点A，B的坐标求出OA，OB的长度，再根据勾股定理求出AB的长，即可得出OC的长，再比较无理数的大小确定点C的横坐标介于哪个区间．
【详解】∵点A，B的坐标分别为（﹣2，0），（0，3），
∴OA＝2，OB＝3，
在Rt△AOB中，由勾股定理得：AB＝
∴AC＝AB＝ ，
∴OC＝﹣2，
∴点C的坐标为（﹣2，0），
∵ ，
∴ ，
即点C的横坐标介于1和2之间，
故选：B．
【点睛】
本题考查了弧与x轴的交点问题，掌握勾股定理、无理数大小比较的方法是解题的关键．
8、A
【分析】根据一次函数解析式系数的正负性判断函数图象经过的象限．
【详解】解：一次函数中．，，
此函数的图象经过一、二、三象限．
故选A．
【点睛】
本题考查一次函数图象经过的象限，解题的关键是掌握一次函数图象的性质．
9、A
【解析】解不等式组得：a10、C
【详解】由题意知，y与x的函数关系为分段函数．
故选C．
考点：1.一次函数的应用；2.一次函数的图象．
11、B
【解析】沿着一条直线折叠后两侧能够完全重合的图形是轴对称图形，根据定义判断即可．
【详解】A不是轴对称图形，不符合题意；
B是轴对称图形，符合题意；
C不是轴对称图形，不符合题意；
D不是轴对称图形，不符合题意；
故选：B．
【点睛】
本题考查轴对称图形的识别，熟记定义是解题的关键．
12、A
【分析】根据关于轴对称的点的特征：横坐标相同，纵坐标互为相反数即可得出答案．
【详解】∵关于轴对称的点横坐标相同，纵坐标互为相反数，
∴点关于轴的对称点的坐标为．
故选：A．
【点睛】
本题主要考查关于轴对称的点的特征，掌握关于轴对称的点的特征是解题的关键．
二、填空题（每题4分，共24分）
13、
【分析】直接根据函数图象交点坐标为两函数解析式组成的方程组的解得到答案．
【详解】∵直线y=ax+b和直线y=kx交点P的坐标为（-4，-2），
∴关于x，y的二元一次方程组组 的解为 ．
故答案为．
【点睛】
此题考查一次函数与二元一次方程（组），解题关键在于掌握图像交点的意义.
14、
【分析】一次函数的交点坐标即是两个一次函数解析式组成的方程组的解，由此即可得到方程组的解.
【详解】∵一次函数y=7－4x和y=1－x的图象的交点坐标为（2，-1），
∴方程组的解为，
故答案为：.
【点睛】
此题考查两个一次函数的交点坐标与方程组的解的关系，正确理解方程组与依次函数的关系是解题的关键.
15、25.5cm尺码的鞋子可以多进一些（答案不唯一，符合实情就行）
【分析】利用众数的意义进行解答即可.
【详解】解：去鞋厂进货时25.5cm尺码型号的鞋子可以多进一些，这组数据中的众数是25.5，故男鞋中型号25.5cm尺码销售较好，25.5cm尺码的鞋子可以多进一些.
故答案为：25.5cm尺码的鞋子可以多进一些. （答案不唯一，符合实情就行）
【点睛】
本题题主要考查了众数的意义，理解众数反映了一组数据的集中程度，是描述一组数据集中趋势的量是解答本题的关键.
16、
【解析】本题的等量关系是：绳长-木长=4.5；木长- 绳长=1，据此可列方程组求解．
【详解】设绳长x尺，长木为y尺，
依题意得，
故答案为：.
【点睛】
此题考查由实际问题抽象出二元一次方程组，解题关键在于列出方程.
17、
【分析】（1）利用等腰三角形的性质和三角形的内角和即可得出结论；
（2）当点E在CA的延长线上，点D在线段BC上，同（1）的方法即可得出结论．
【详解】（1）设∠ABC=x，∠AED=y，
∵,,
∴∠ACB=∠ABC, ∠AED=∠ADE
∴∠ACB=x，∠ADE=y，
在△DEC中，∵∠ AED=∠ACB+∠EDC,
∴y=β+x，
在△ABD中，∵∠ADC=∠BAD+∠ABC, ∠ADC=∠ADE+∠EDC=∠AED+∠EDC,
∴α+x=y+β=β+x+β，
∴α=2β；
故答案为：α=2β；
（2）当点E在CA的延长线上，点D在线段BC上，
设∠ABC=x，∠ADE=y，
∵,,
∴∠ACB=∠ABC, ∠AED=∠ADE,
∴∠ACB=x，∠AED=y，
在△ABD中，∵∠ADC=∠BAD+∠ABC, ∠ADC=∠EDC-∠ADE,
∴x+α=β-y，
在△DEC中，∵∠ECD+∠CED+∠EDC=180°,
∴x+y+β=180°，
∴α=2β-180°；
故答案为α=2β-180°．
【点睛】
此题主要考查了等腰三角形的性质，三角形的内角和定理，解本题的关键是利用三角形的内角和定理得出等式．
18、AB=AC
【解析】解：还需添加条件AB=AC．∵AD⊥BC于D，∴∠ADB=∠ADC=90°．在Rt△ABD和Rt△ACD中，∵AB=AC，AD=AD，∴Rt△ABD≌Rt△ACD（HL）．故答案为AB=AC．
三、解答题（共78分）
19、 (1)；(2)
【分析】（1）原式先计算乘方运算，再计算乘除运算即可得到结果；
（2）原式括号中两项通分后利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．
【详解】解：（1）原式；
（2）原式．
【点睛】
此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
20、（1）见解析；（2）见解析
【分析】（1）根据题意证明△ADB≌△ADC即可证明AB＝AC；
（2）连接BC，由中垂线的逆定理证明即可．
【详解】证明：（1）∵在△ADB和△ADC中，
，
∴△ADB≌△ADC（AAS），
∴AB＝AC；
（2）连接BC，
∵△ADB≌△ADC，
∴AB＝AC，BD＝CD，
∴A和D都在线段BC的垂直平分线上，
∴AD是线段BC的垂直平分线，
即AD⊥BC．
【点睛】
本题主要考查全等三角形的判定与性质以及中垂线的逆定理，熟记相关定理是解题关键．
21、（1）作图见见解析；（2）100°．
【解析】试题分析：（1）根据题意作出图形即可；
（2）由于DE是AB的垂直平分线，得到AE=BE，根据等腰三角形的性质得到∠EAB=∠B=50°，由三角形的外角的性质即可得到结论．
试题解析：（1）如图所示：
（2）∵DE是AB的垂直平分线，
∴AE=BE，
∴∠EAB=∠B=50°，
∴∠AEC=∠EAB+∠B=100°．
22、（1）FH＝GH，FH⊥HG；（2）△FGP是等腰直角三角形，理由见解析；（3）2
【分析】（1）直接利用三角形的中位线定理得出FH＝GH，再借助三角形的外角的性质即可得出∠FHG＝90°，即可得出结论；
（2）由题意可证△CAD≌△CBE，可得∠CAD＝∠CBE，AD＝BE，根据三角形中位线定理，可证HG＝HF，HF∥AD，HG∥BE，根据角的数量关系可求∠GHF＝90°，即可证△FGH是等腰直角三角形；
（3）由题意可得S△HGF最大＝HG2，HG最大时，△FGH面积最大，点D在AC的延长线上，即可求出△FGH面积的最大值．
【详解】解：（1）∵AC＝BC，CD＝CE，
∴AD＝BE，
∵点F是DE的中点，点H是AE的中点，
∴FH＝AD，
∵点G是AB的中点，点H是AE的中点，
∴GH＝BE，
∴FH＝GH，
∵点F是DE的中点，点H是AE的中点，
∴FH∥AD，
∴∠FHE＝∠CAE
∵点G是AB的中点，点H是AE的中点，
∴GH∥BE，
∴∠AGH＝∠B，
∵∠C＝90°，AC＝BC，
∴∠BAC＝∠B＝45°，
∵∠EGH＝∠B+∠BAE，
∴∠FHG＝∠FHE+∠EHG＝∠CAE+∠B+∠BAE＝∠B+∠BAC＝90°，
∴FH⊥HG，
故答案为：FH＝GH，FH⊥HG；
（2）△FGP是等腰直角三角形
理由：由旋转知，∠ACD＝∠BCE，
∵AC＝BC，CD＝CE，
∴△CAD≌△CBE（SAS），
∴∠CAD＝∠CBE，AD＝BE，
由三角形的中位线得，HG＝BE，HF＝AD，
∴HG＝HF，
∴△FGH是等腰三角形，
由三角形的中位线得，HG∥BE，
∴∠AGH＝∠ABE，
由三角形的中位线得，HF∥AD，
∴∠FHE＝∠DAE，
∵∠EHG＝∠BAE+∠AGH＝∠BAE+∠ABE，
∴∠GHF＝∠FHE+∠EHG
＝∠DAE+∠BAE+∠ABE
＝∠BAD+∠ABE
＝∠BAC+∠CAD+∠ABC﹣∠CBE
＝∠CBA+∠CAB，
∵∠ACB＝90°，AC＝BC，
∴∠CBA＝∠CAB＝45°，
∴∠GHF＝90°，
∴△FGH是等腰直角三角形；
（3）由（2）知，△FGH是等腰直角三角形，HG＝HF＝AD，
∵S△HGF＝HG2，
∴HG最大时，△FGH面积最大，
∴点D在AC的延长线上，
∵CD＝4，AC＝8
∴AD＝AC+CD＝12，
∴HG＝×12＝1．
∴S△PGF最大＝HG2＝2．
【点睛】
此题是几何变换综合题，主要考查了等腰直角三角形的判定和性质，全等三角形的判定和性质，旋转的性质，三角形的中位线定理，判断出HG⊥FH是解本题的关键．
23、，1
【分析】先将分式的分子和分母分解因式，再根据分式的化简求值的过程计算即可求解．
【详解】解：原式＝，
，
，
.
∵a≤1的非负整数解有0，1，1，
又∵a≠1，1，
∴当a＝0时，原式＝1．
【点睛】
此题考察分式的化简求值，化简时需先分解因式约去公因式得到最简分式，求值时选的数需满足分母不为0的数才可代入求值.
24、（1）50°；（2）见解析
【解析】试题分析：⑴根据等腰三角形的性质、三角形的内角和定理与四边形的内角和为360°，可求得所求角的度数.
⑵连接BF，根据三角形内角和定理与等腰三角形三线合一，可知.
试题解析：⑴ ∵∠AFD=155°，∴∠DFC=25°，∵DF⊥BC，DE⊥AB，
∴∠FDC=∠AED=90°，
在Rt△EDC中，∴∠C=90°﹣25°=65°，
∵AB=BC，∴∠C=∠A=65°，
∴∠EDF=360°﹣65°﹣155°﹣90°=50°．
⑵ 连接BF，∵AB=BC，且点F是AC的中点，
∴BF⊥AC，，
∴∠CFD+∠BFD=90°，∠CBF+∠BFD=90°，
∴∠CFD=∠CBF，
∴．
25、（1）50元；（2）900元．
【解析】试题分析：（1）等量关系为：4月份营业数量=5月份营业数量﹣20；
（2）算出4月份的数量，进而求得成本及每件的盈利，进而算出5月份的售价及每件的盈利，乘以5月份的数量即为5月份的获利．
解：（1）设该种纪念品4月份的销售价格为x元．
根据题意得，
20x=1000
解之得x=50，
经检验x=50是原分式方程的解，且符合实际意义，
∴该种纪念品4月份的销售价格是50元；
（2）由（1）知4月份销售件数为（件），
∴四月份每件盈利（元），
5月份销售件数为40+20=60件，且每件售价为50×0.9=45（元），每件比4月份少盈利5元，为20﹣5=15（元），
所以5月份销售这种纪念品获利60×15=900（元）．
考点：分式方程的应用．
26、7元/千克
【分析】设这种大米原价是每千克x元，根据题意列出分式方程，解出并检验即可.
【详解】解：设这种大米原价是每千克x元，
根据题意得： ，
解得x=7 经检验x=7是原分式方程的解，
答：这种大米的原价是7元/千克.
【点睛】
此题主要考查了分式方程的应用，弄清题意，找准等量关系列出方程是解题的关键.
尺码/
销量/双