辽宁省辽河油田欢喜岭第二初级中学2023-2024学年九上数学期末教学质量检测试题含答案

这是一份辽宁省辽河油田欢喜岭第二初级中学2023-2024学年九上数学期末教学质量检测试题含答案，共10页。试卷主要包含了已知2a＝3b等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图，AB是一垂直于水平面的建筑物，某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度（或坡比）为i=1：0.75、坡长为10米的斜坡CD到达点D，然后再沿水平方向向右行走40米到达点E（A，B，C，D，E均在同一平面内）．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为（参考数据：sin24°≈0.41，cs24°≈0.91，tan24°=0.45）（ ）
A．21.7米B．22.4米C．27.4米D．28.8米
2．如图，一次函数和反比例函数的图象相交于，两点，则使成立的取值范围是( )
A．或B．或
C．或D．或
3．已知二次函数y＝﹣2x2﹣4x+1，当﹣3≤x≤2时，则函数值y的最小值为（ ）
A．﹣15B．﹣5C．1D．3
4．为测量某河的宽度，小军在河对岸选定一个目标点A，再在他所在的这一侧选点B，C，D，使得AB⊥BC，CD⊥BC，然后找出AD与BC的交点E，如图所示．若测得BE＝90 m，EC＝45 m，CD＝60 m，则这条河的宽AB等于( )
A．120 mB．67.5 mC．40 mD．30 m
5．如图，在平面直角坐标系中，已知点的坐标是，点是曲线上的一个动点，作轴于点，当点的橫坐标逐渐减小时，四边形的面积将会（ ）
A．逐渐增大B．不变C．逐渐减小D．先减小后增大
6．如图是二次函数y＝ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x＝﹣1．给出四个结论：①b2＞4ac；②2a+b＝0；③a﹣b+c＝0；④5a＜b．其中正确的有（ ）
A．1个B．2个C．3个D．4个
7．如图，D是等边△ABC边AD上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E、F分别在AC、BC上，则CE：CF=（ ）
A．B．C．D．
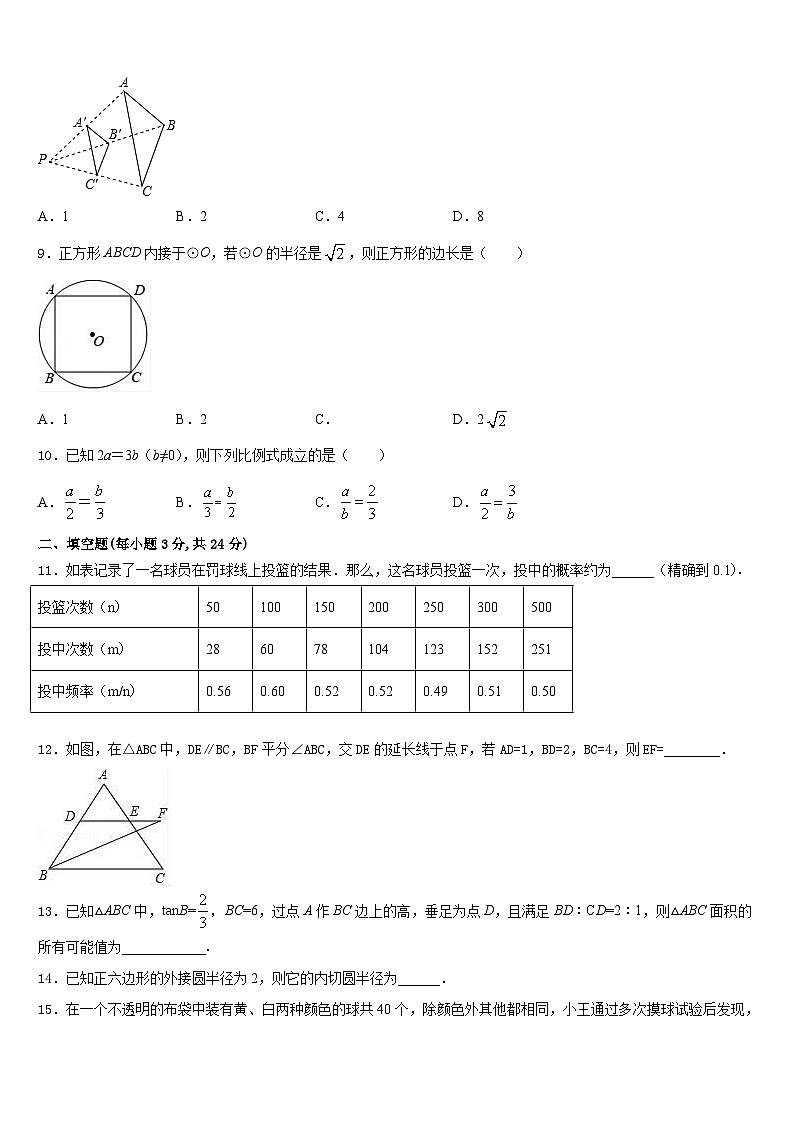
8．如图，△ABC与△A′B′C′是位似图形，PB′＝BB′，A′B′＝2，则AB的长为（ ）
A．1B．2C．4D．8
9．正方形ABCD内接于⊙O，若⊙O的半径是，则正方形的边长是（ ）
A．1B．2C． D．2
10．已知2a＝3b（b≠0），则下列比例式成立的是（ ）
A．＝B．C．D．
二、填空题(每小题3分,共24分)
11．如表记录了一名球员在罚球线上投篮的结果．那么，这名球员投篮一次，投中的概率约为______（精确到0.1）．
12．如图，在△ABC中，DE∥BC，BF平分∠ABC，交DE的延长线于点F，若AD=1，BD=2，BC=4，则EF=________．
13．已知△ABC中，tanB=，BC=6，过点A作BC边上的高，垂足为点D，且满足BD：CD=2：1，则△ABC面积的所有可能值为____________．
14．已知正六边形的外接圆半径为2，则它的内切圆半径为______．
15．在一个不透明的布袋中装有黄、白两种颜色的球共40个，除颜色外其他都相同，小王通过多次摸球试验后发现，摸到黄球的频率稳定在0.35左右，则布袋中黄球可能有_________个
16．如图，点、、…在反比例函数的图象上，点、、……在反比例函数的图象上，，且，则（为正整数）的纵坐标为______．（用含的式子表示）
17．在一个不透明的袋子中装有除颜色外其余均相同的7个小球，其中红球2个，黑球5个，若再放入m个一样的黑球并摇匀，此时，随机摸出一个球是黑球的概率等于，则m的值为 ．
18．如图示，在中，，，，点在内部，且，连接，则的最小值等于______.
三、解答题(共66分)
19．（10分）如图，一次函数y＝kx＋b的图象与反比例函数y＝(x＞0)的图象交于点P(n，2)，与x轴交于点A(－4，0)，与y轴交于点C，PB⊥x轴于点B，点A与点B关于y轴对称．
（1）求一次函数，反比例函数的表达式；
（2）求证：点C为线段AP的中点；
（3）反比例函数图象上是否存在点D，使四边形BCPD为菱形．如果存在，说明理由并求出点D的坐标；如果不存在，说明理由．
20．（6分）阅读理解，我们已经学习了点和圆、直线和圆的位置关系以及各种位置关系的数量表示，如下表：
类似于研究点和圆、直线和圆的位置关系，我们也可以用两圆的半径和两圆的圆心距（两圆圆心的距离）来刻画两圆的位置关系．如果两圆的半径分别为和（r1＞r2），圆心距为d，请你通过画图，并利用d与和之间的数量关系探索两圆的位置关系．
21．（6分）把下列多项式分解因式：
（1）．
（2）．
22．（8分）如图，在△中，，，点从点出发，沿以每秒的速度向点运动，同时点从点出发，沿以的速度向点运动，设运动时间为秒
（1）当为何值时，．
（2）当为何值时，∥．
（3）△能否与△相似？若能，求出的值；若不能，请说明理由．
23．（8分）如图，在ABC中，点D，E分别在边AC，AB上，且AE·AB＝AD·AC，连接DE，BD.
（1）求证：ADE~ABC.
（2）若点E为AB为中点，AD：AE＝6：5，ABC的面积为50，求BCD面积.
24．（8分）某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件
（1）写出商场销售这种文具，每天所得的销售利润（元）与销售单价（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；
（3）商场的营销部结合上述情况，提出了A、B两种营销方案
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元
请比较哪种方案的最大利润更高，并说明理由
25．（10分）如图，在正方形中，，点在正方形边上沿运动（含端点），连接，以为边，在线段右侧作正方形，连接、.
小颖根据学习函数的经验，在点运动过程中，对线段、、的长度之间的关系进行了探究.
下面是小颖的探究过程，请补充完整：
（1）对于点在、边上的不同位置，画图、测量，得到了线段、、的长度的几组值，如下表：
在、和的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数.
（2）在同一平面直角坐标系中，画出（1）中所确定的函数的图象：
（3）结合函数图像，解决问题：
当为等腰三角形时，的长约为
26．（10分）我县寿源壹号楼盘准备以每平方米元均价对外销售，由于国务院有关房地产的新政策出台，购房者持币观望，房地产开发商为了加快资金周转，对价格进行两次下调后，决定以每平方米元的均价开盘销售．
（1）求平均每次下调的百分率．
（2）某人准备以开盘均价购买一套平方米的住房，开发商给予以下两种优惠方案供选择：
①打折销售；
②不打折，一次性送装修费每平方米元．
试问哪种方案更优惠？
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、A
4、A
5、C
6、B
7、B
8、C
9、B
10、B
二、填空题(每小题3分,共24分)
11、0.1
12、
13、8或1．
14、
15、14
16、
17、1．
18、
三、解答题(共66分)
19、（1）y＝x＋1；y＝（2）证明见解析；（3）存在，D（8，1）．
20、见解析
21、（1）；（2）
22、（1）秒；（2）秒；（3）能，秒或5秒
23、 (1)详见解析； (2)14
24、 (1) w＝－10x2＋700x－10000;(2) 即销售单价为35元时，该文具每天的销售利润最大;
(3) A方案利润更高.
25、（1）；（2）画图见解析；（3）或或
26、（1）10%；（2）选择方案①更优惠．
投篮次数（n）
50
100
150
200
250
300
500
投中次数（m）
28
60
78
104
123
152
251
投中频率（m/n）
0.56
0.60
0.52
0.52
0.49
0.51
0.50
图形表示
（圆和圆的位置关系）
数量表示
（圆心距d与两圆的半径、的数量关系）

位置
位置
位置
位置
位置
位置
位置