

- 冀教版数学九上 第二十五章 学情评估卷 试卷 0 次下载
- 冀教版数学九上 第二十六章 学情评估卷 试卷 0 次下载
- 冀教版数学九上 第二十七章 学情评估卷 试卷 0 次下载
- 冀教版数学九上 第二十八章 学情评估卷 试卷 0 次下载
- 冀教版数学九上 期末 学情评估卷 试卷 0 次下载
冀教版数学九上 期中 学情评估卷
展开2.若eq \f(x,y)=eq \f(2,5),则eq \f(x,x+y)的值为( )
A.eq \f(2,7) B.eq \f(3,7) C.eq \f(7,2) D.eq \f(7,3)
3.学校食堂有15元、18元、20元三种盒饭供学生选择(每人购买一份).某天盒饭的销售情况如图所示,则当天学生购买盒饭费用的平均数是( )
A.15元 B.16元 C.17元 D.18元
(第3题) (第4题)
4.如图是某商店售卖的花架,其中AD∥BE∥CF,DE=24 cm,EF=32 cm,BC=40 cm,则AB的长为( )
A.eq \f(80,3) cm B.eq \f(100,3) cm C.50 cm D.30 cm
5.小颖随机抽查她家6月份某5天的日用电量(单位:度),结果如下:9,11,7,10,8.根据这些数据,估计她家6月份的用电量为( )
A.180度 B.210度 C.240度 D.270度
6.为增强同学们的体质,丰富校园文化体育生活,某校八年级举行了篮球比赛,比赛以循环赛的形式进行,即每个班级之间都要比赛一场,共比赛了45场,则该校八年级的班级数有( )
A.9个 B.10个 C.5个 D.8个
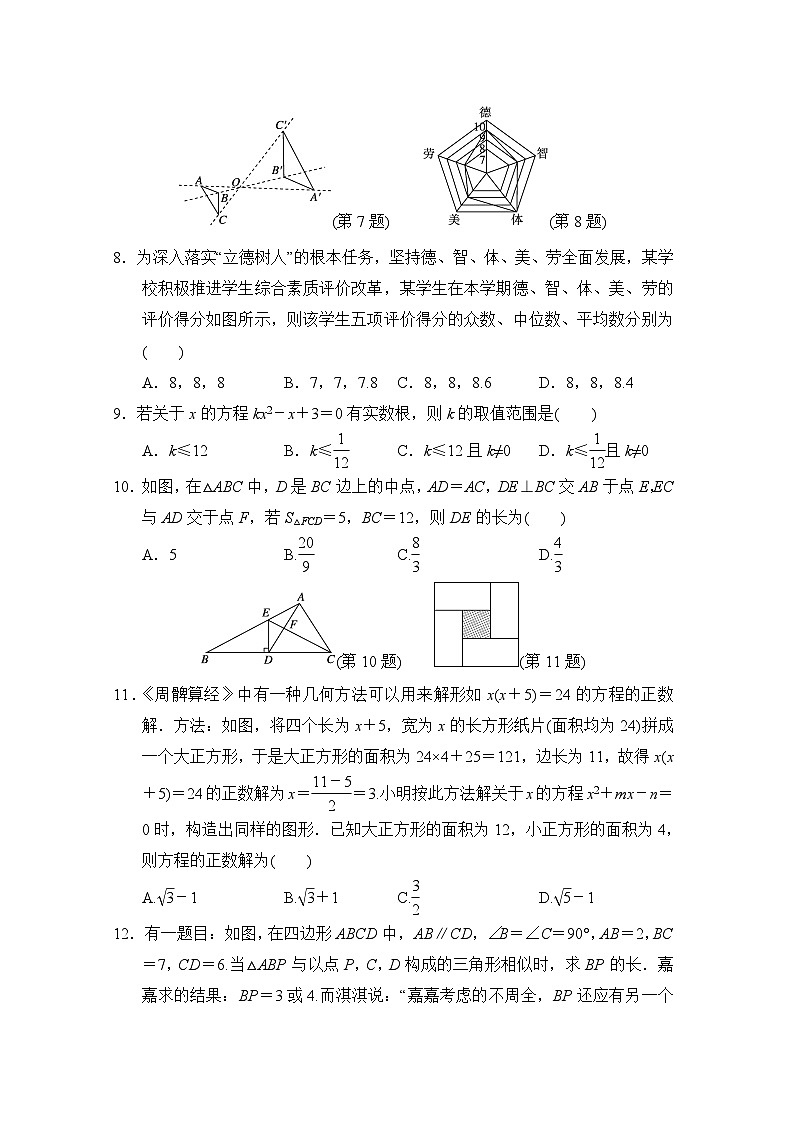
7.如图,以点O为位似中心,把△ABC的各边长放大为原来的2倍得到△A′B′C′,以下说法中错误的是( )
A.AO∶AA′=1∶2 B.点A,O,A′三点在同一条直线上
C.S△ABC∶S△A′B′C′=1∶4 D.BC∥B′C′
(第7题) (第8题)
8.为深入落实“立德树人”的根本任务,坚持德、智、体、美、劳全面发展,某学校积极推进学生综合素质评价改革,某学生在本学期德、智、体、美、劳的评价得分如图所示,则该学生五项评价得分的众数、中位数、平均数分别为( )
A.8,8,8 B.7,7,7.8 C.8,8,8.6 D.8,8,8.4
9.若关于x的方程kx2-x+3=0有实数根,则k的取值范围是( )
A.k≤12 B.k≤eq \f(1,12) C.k≤12且k≠0 D.k≤eq \f(1,12)且k≠0
10.如图,在△ABC中,D是BC边上的中点,AD=AC,DE⊥BC交AB于点E,EC与AD交于点F,若S△FCD=5,BC=12,则DE的长为( )
A.5 B.eq \f(20,9) C.eq \f(8,3) D.eq \f(4,3)
(第10题) (第11题)
11.《周髀算经》中有一种几何方法可以用来解形如x(x+5)=24的方程的正数解.方法:如图,将四个长为x+5,宽为x的长方形纸片(面积均为24)拼成一个大正方形,于是大正方形的面积为24×4+25=121,边长为11,故得x(x+5)=24的正数解为x=eq \f(11-5,2)=3.小明按此方法解关于x的方程x2+mx-n=0时,构造出同样的图形.已知大正方形的面积为12,小正方形的面积为4,则方程的正数解为( )
A.eq \r(3)-1 B.eq \r(3)+1 C.eq \f(3,2) D.eq \r(5)-1
12.有一题目:如图,在四边形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6.当△ABP与以点P,C,D构成的三角形相似时,求BP的长.嘉嘉求的结果:BP=3或4.而淇淇说:“嘉嘉考虑的不周全,BP还应有另一个不同的值.”下列说法正确的是( )
(第12题)
A.淇淇说得对,且BP的另一个值是eq \f(7,4)
B.淇淇说得不对,BP就等于3或4
C.嘉嘉求的结果不对,BP应等于3或5
D.两人都不对,BP应有4个不同的值
二、填空题(本大题共4小题,每小题3分,共12分)13.一元二次方程x2-6x-7=0的解是__________.
14.小聪同学在计算一组数据1、3、4、5、x的方差时,写出的计算过程是s2=eq \f(1,5)×[(1-4)2+(3-4)2+(4-4)2+(5-4)2+(x-4)2]=4,如果他的计算是正确的,那么这组数据中的x为________.
15.已知x1,x2是关于x的方程x2+ax-2b=0的两个实数根,且x1+x2=-2,x1x2=1,则ba的值为________.
16.如图,已知在△ABC中,AB=AC=5,BC=8,点P在边BC上(点P与点B,C不重合),射线PF与边AC交于点F,过点A作BC的
平行线,交射线PF于点Q,∠APF=∠B.
(1)若BP=2,则CF的长为________;
(2)当△AFQ是等腰三角形时,BP的长为________.
三、解答题(本大题共8小题,共72分.解答时应写出文字说明、证明过程或演算步骤)17.(7分)小明在解方程x2-2x=1时出现了错误,解答过程如下:
解:x2-2x+1=1,…第一步
(x-1)2=1,…第二步
x-1=±1,…第三步
x1=0,x2=2.…第四步
(1)小明解该方程的方法是________法,小明的解答过程从第________步开始出错,其错误的原因是__________________________________________;
(2)请你写出此题正确的解答过程.
18.(8分)如图,在▱ABCD中,E为BC的中点,连接AE交对角线BD于点F.
(1)求△ADF与△EBF的面积比;
(2)若△ADF的周长为24,求△EBF的周长.
19.(8分)某公司欲招聘一名英语翻译,对甲、乙、丙三人进行口语、面试、笔试三项测试,成绩高者被录用,三人的成绩(单位:分)如下表:
(1)如果公司将口语成绩、面试成绩、笔试成绩的平均数作为最终成绩,则甲与丙的最终成绩相同,求m的值;
(2)若m的值为(1)中所求,且将甲、乙、丙三人的三项测试成绩,按照扇形统计图各项所占之比来计算最终成绩,请分别计算三人的最终成绩,并判断录用结果.
20.(8分)已知关于x的一元二次方程ax2-3x+1=0有两个不相等的实数根x1,x2.
(1)求a的取值范围;
(2)若a=-2,用公式法求该方程的解.
21.(9分)【学科融合】如图①,在光的反射现象中,反射光线、入射光线和法线都在同一个平面内,反射光线和入射光线分别位于法线两侧,反射角r等于入射角i,这就是光的反射定律.
【问题解决】如图②,林舒同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电筒的灯泡在点G处,手电筒的光从平面镜上的点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点G到地面的高度GA=1.2 m,点F到地面的高度FC=1.5 m,灯泡到木板的水平距离AC=5.4 m,木板到墙的水平距离CD=4 m.点A,B,C,D在同一条直线上.
(1)求平面镜上的点B与木板的水平距离BC的长;
(2)求点E到地面的高度ED.
22.(10分)为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该校九年级m名学生,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图①)和扇形统计图(图②).
(1)根据信息回答下列问题:
①求m的值;
②求扇形统计图中每周平均课外阅读时间为5小时所在扇形的圆心角的度数;
③补全条形统计图.
(2)这组数据的众数为________小时,中位数为________小时.
(3)若该年级总共有900名学生,则每周平均课外阅读时间为3小时的大约有多少名学生?
23.(10分)“一盔一带”安全守护行动在全国各地积极开展.某品牌头盔的销量逐月攀升,某超市以每个20元的进价购进一批该品牌头盔,当该品牌头盔的售价为30元/个时,该超市七月销售200个,八、九月该品牌头盔销量持续上涨,在售价不变的基础上,九月的销量达到288个.
(1)求八、九两月销量的月平均增长率.
(2)十月该超市为了减少库存,开始降价促销,经调查发现,该品牌头盔每个的售价每降低1元,月销量在九月销量的基础上增加3个.设该品牌头盔每个降价a元.
①每个头盔的利润为________元,该月的销量是________个;(请用含a的代数式表示)
②若该超市十月能获利1 800元,则每个头盔的售价是多少元?
24.(12分)(1)问题背景:如图①,∠ACB=∠ADE=90°,AC=BC,AD=DE,求证:△ABE∽△ACD;
(2)尝试应用:如图②,将正方形ABCD的边AB,BC绕点A逆时针旋转一定角度,得到线段AE,EF,连接AF交CD于点H,连接BE,CF,若△ABE∽△CFH,求∠BAE的度数;
(3)拓展创新:如图③,在四边形ABCD中,∠BAC=30°,∠ABC=90°,∠ADC=60°,AD=1,BD=2.求CD的长.
答案
一、选择题
二、填空题
13.x1=7,x2=-1 14.7 15.eq \f(1,4)
16.(1)eq \f(12,5) (2)5或eq \f(25,8) 解析:(1)∵AB=AC,
∴∠B=∠C.
∵∠B=∠APF,∠APC=∠B+∠BAP=∠APF+∠FPC,
∴∠BAP=∠FPC,∴△ABP∽△PCF,
∴eq \f(CF,BP)=eq \f(CP,AB).∵BP=2,BC=8,
∴CP=BC-BP=8-2=6,
∴eq \f(CF,2)=eq \f(6,5),∴CF=eq \f(12,5).
(2)情况1:如图①,当AF=FQ时,即∠FAQ=∠FQA.
∵AQ∥BC,∴∠FQA=∠FPC,∠FAQ=∠C.
∵AB=AC,∴∠B=∠C.
∴∠FPC=∠FQA=∠FAQ=∠C=∠B,∴AB∥PQ.
∴四边形ABPQ是平行四边形,
∴PQ=AB=5,AQ=BP.
∵∠APQ=∠B,∠FQA=∠C,
∴△APQ∽△ABC,
∴eq \f(AQ,AC)=eq \f(PQ,BC).∴eq \f(BP,5)=eq \f(5,8).∴BP=eq \f(25,8).
情况2:如图②,当AQ=AF时,即∠AQF=∠AFQ.
∵∠AFQ=∠PFC,∠AQF=∠FPC,
∴∠CFP=∠CPF.
∴CP=CF.
由(1)得△ABP∽△PCF,
∴eq \f(AB,CP)=eq \f(BP,CF).
∴BP=AB=5.
情况3:如图③,当AQ=QF时,即∠QAF=∠QFA.
∵∠QFA=∠PFC,∠QAF=∠C,∴∠PFC=∠C.
∵∠C=∠B=∠APQ,
∴∠APQ=∠PFC,
∴AP∥CF,与已知矛盾,舍去.
综上所述,BP的长为5或eq \f(25,8).
三、解答题
17.解:(1)配方;一;等号右边没有加1
(2)正确的解答过程如下:x2-2x+1=1+1,(x-1)2=2,x-1=±eq \r(2),∴x1=1+eq \r(2),x2=1-eq \r(2).
18.解:(1)∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,∴∠ADF=∠EBF,∠DAF=∠AEB,
∴△DAF∽△BEF.∵E为BC的中点,∴AD=BC=2BE,∴eq \f(S△ADF,S△EBF)=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(AD,BE)))eq \s\up12(2)=eq \f(4,1).
(2)由(1)知△DAF∽△BEF,且AD=2BE,∴eq \f(C△ADF,C△EBF)=eq \f(AD,BE)=eq \f(2,1).
∵△ADF的周长为24,∴△EBF的周长为12.
19.解:(1)根据题意,得eq \f(87+90+90,3)=eq \f(m+93+84,3),解得m=90.
(2)∵口语成绩所占比例为eq \f(180°,360°)=eq \f(1,2),
面试成绩所占比例为eq \f(120°,360°)=eq \f(1,3),
笔试成绩所占比例为eq \f(60°,360°)=eq \f(1,6),
∴口语成绩、面试成绩、笔试成绩的比为3∶2∶1.
∴甲的最终成绩为eq \f(87×3+90×2+90×1,3+2+1)=88.5(分),
乙的最终成绩为eq \f(93×3+84×2+87×1,3+2+1)=89(分),
丙的最终成绩为eq \f(90×3+93×2+84×1,3+2+1)=90(分).
∵90>89>88.5,∴录用丙.
20.解:(1)∵关于x的一元二次方程ax2-3x+1=0有两个不相等的实数根,∴(-3)2-4a>0,且a≠0,
解得a
即x1=eq \f(-3+\r(17),4),x2=eq \f(-3-\r(17),4).
21.解:(1)根据题意,得∠FBC=∠GBA,
又∵∠FCB=∠GAB=90°,∴△BFC∽△BGA,
∴eq \f(CF,AG)=eq \f(BC,AB),即eq \f(1.5,1.2)=eq \f(BC,5.4-BC),解得BC=3 m,
∴平面镜上的点B与木板的水平距离BC的长为3 m.
(2)由题意,得DE∥CF,∴△BFC∽△BED,
∴eq \f(CF,DE)=eq \f(BC,BD),∴eq \f(1.5,DE)=eq \f(3,3+4),解得DE=3.5 m,
∴点E到地面的高度ED为3.5 m.
22.解:(1)①∵每周平均课外阅读时间为2小时所在扇形的圆心角的度数为90°,∴其所占的百分比为eq \f(90°,360°)=eq \f(1,4)=25%.
∵每周平均课外阅读时间为2小时的有15名学生,
∴m=15÷25%=60.
②eq \f(5,60)×360°=30°.
③每周平均课外阅读时间为3小时的人数为60-10-15-10-5=20(名),补全条形统计图如图所示.
(2)3;3 (3)900×eq \f(20,60)=300(名).
答:每周平均课外阅读时间为3小时的大约有300名学生.
23.解:(1)设八、九两月销量的月平均增长率为x,
由题意,得200(1+x)2=288,
解得x1=0.2=20%,x2=-2.2(不符合题意,舍去).
答:八、九两月销量的月平均增长率为20%.
(2)①(10-a);(288+3a)
②由题意,得(10-a)(288+3a)=1 800,
整理,得a2+86a-360=0,解得a1=4,a2=-90(不符合题意,舍去),∴a=4,则每个头盔的售价为30-4=26(元).
答:每个头盔的售价是26元.
24.(1)证明:∵∠ACB=∠ADE=90°,AC=BC,AD=DE,
∴AB=eq \r(AC2+BC2)=eq \r(2)AC,AE=eq \r(AD2+DE2)=eq \r(2)AD,∠CAB=∠DAE=45°.∴∠CAB-∠BAD=∠DAE-∠BAD,即∠CAD=∠BAE.
∵eq \f(AB,AC)=eq \f(AE,AD)=eq \r(2),∴△ABE∽△ACD.
(2)解:如图①,连接AC,∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°.∴∠ACD=45°.
由旋转的性质可得AE=AB,∠BAE=∠CAF,
∴∠ABE=∠AEB.∵△ABE∽△CFH,∴∠FCH=∠BAE,∠CFH=∠ABE=∠AEB=∠CHF.
设∠BAE=∠CAF=∠FCH=x,
则∠CHF=∠CFH=eq \f(180°-x,2).∵∠ACD=45°,∠ACF+∠AFC+∠CAF=180°,∴∠ACD+∠HCF+∠AFC+∠CAF=180°,即45°+x+eq \f(180°-x,2)+x=180°,
解得x=30°,∴∠BAE=30°.
(3)解:如图②,过点B作BE⊥BD,连接DE,使得∠BDE=30° ,连接CE,过点E作EF⊥CD交DC的延长线于点F,
∵∠ABC=∠DBE=90°,∠BAC=∠BDE=30°,
∴AC=2BC,DE=2BE,∠ABC-∠DBC=∠DBE-∠DBC.
∴AB=eq \r(AC2-BC2)=eq \r(3)BC,BD=eq \r(DE2-BE2)=eq \r(3)BE,∠ABD=∠CBE.
∴eq \f(AB,BC)=eq \f(BD,BE)=eq \r(3).∴△ABD∽△CBE.
∴eq \f(AD,CE)=eq \f(BD,BE)=eq \r(3),∠BCE=∠BAD.
∴CE=eq \f(AD,\r(3))=eq \f(1,\r(3))=eq \f(\r(3),3).
在Rt△DBE中,BD=2,∠DBE=90°,∠BDE=30°,
∴BE2+22=4BE2,解得BE=eq \f(2 \r(3),3)(负值舍去).
∴DE=2BE=eq \f(4 \r(3),3).
∵∠ABC=90°,∠ADC=60°,
∴∠BAD+∠BCD=360°-∠ABC-∠ADC=210°,
∴∠BCE+∠BCD=210°,
∴∠DCE=360°-(∠BCE+∠BCD)=150°,
∴∠ECF=180°-∠DCE=30°,∴EF=eq \f(1,2)CE=eq \f(\r(3),6),
∴CF=eq \r(CE2-EF2)=eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),3)))\s\up12(2)-\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),6)))\s\up12(2))=eq \f(1,2).
在Rt△DEF中,由勾股定理得DF=eq \r(DE2-EF2)=eq \f(\r(21),2),
∴CD=DF-CF=eq \f(\r(21)-1,2).
应聘者
口语成绩
面试成绩
笔试成绩
甲
87
90
90
乙
93
84
87
丙
m
93
84
答案
速查
1
2
3
4
5
6
7
8
9
10
11
12
D
A
C
D
D
B
A
D
B
B
A
A
湘教版数学九上 第一学期期中学情评估: 这是一份湘教版数学九上 第一学期期中学情评估,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
沪科版数学九上 期末学情评估: 这是一份沪科版数学九上 期末学情评估,共12页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
华师版数学九上 期末学情评估: 这是一份华师版数学九上 期末学情评估,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













