北师大版数学九上 期末综合素质评价试卷

这是一份北师大版数学九上 期末综合素质评价试卷，共14页。试卷主要包含了选择题，四象限 D．第三，解答题等内容，欢迎下载使用。

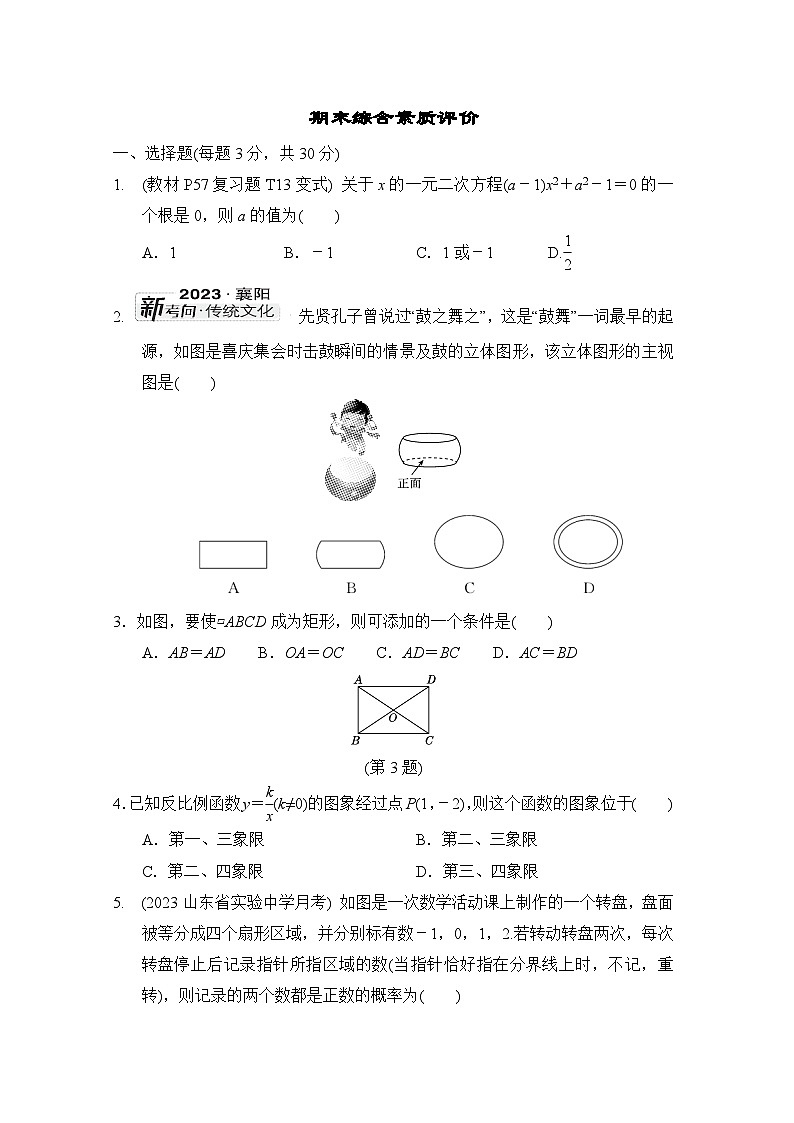
1. (教材P57复习题T13变式) 关于x的一元二次方程(a－1)x2＋a2－1＝0的一个根是0，则a的值为( )
A．1 B．－1 C．1或－1 D.eq \f(1,2)
2. 先贤孔子曾说过“鼓之舞之”，这是“鼓舞”一词最早的起源，如图是喜庆集会时击鼓瞬间的情景及鼓的立体图形，该立体图形的主视图是( )

3．如图，要使▱ABCD成为矩形，则可添加的一个条件是( )
A．AB＝AD B．OA＝OC C．AD＝BC D．AC＝BD
(第3题)
4．已知反比例函数y＝eq \f(k,x)(k≠0)的图象经过点P(1，－2)，则这个函数的图象位于( )
A．第一、三象限 B．第二、三象限
C．第二、四象限 D．第三、四象限
5. (2023山东省实验中学月考) 如图是一次数学活动课上制作的一个转盘，盘面被等分成四个扇形区域，并分别标有数－1，0，1，2.若转动转盘两次，每次转盘停止后记录指针所指区域的数(当指针恰好指在分界线上时，不记，重转)，则记录的两个数都是正数的概率为( )
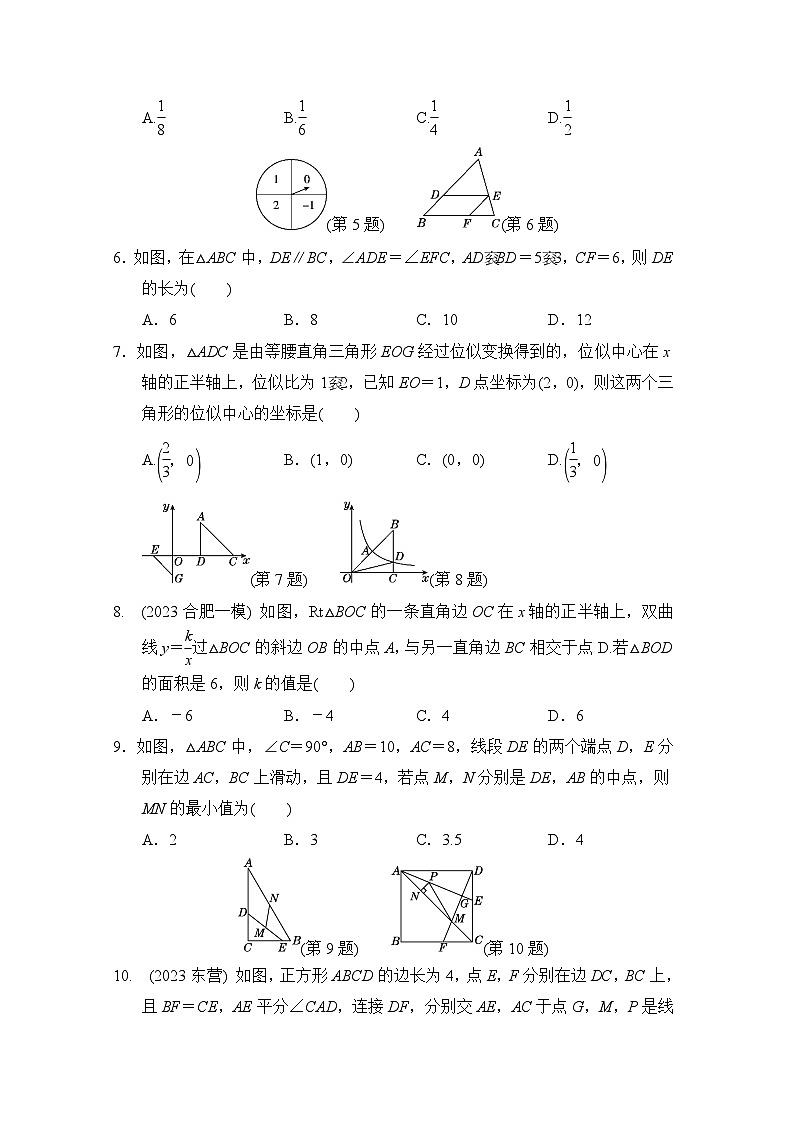
A.eq \f(1,8) B.eq \f(1,6) C.eq \f(1,4) D.eq \f(1,2)
(第5题) (第6题)
6．如图，在△ABC中，DE∥BC，∠ADE＝∠EFC，ADBD＝53，CF＝6，则DE的长为( )
A．6 B．8 C．10 D．12
7．如图，△ADC是由等腰直角三角形EOG经过位似变换得到的，位似中心在x轴的正半轴上，位似比为12，已知EO＝1，D点坐标为(2，0)，则这两个三角形的位似中心的坐标是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)，0)) B．(1，0) C．(0，0) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，0))
(第7题) (第8题)
8. (2023合肥一模) 如图，Rt△BOC的一条直角边OC在x轴的正半轴上，双曲线y＝eq \f(k,x)过△BOC的斜边OB的中点A，与另一直角边BC相交于点D.若△BOD的面积是6，则k的值是( )
A．－6 B．－4 C．4 D．6
9．如图，△ABC中，∠C＝90°，AB＝10，AC＝8，线段DE的两个端点D，E分别在边AC，BC上滑动，且DE＝4，若点M，N分别是DE，AB的中点，则MN的最小值为( )
A．2 B．3 C．3.5 D．4
(第9题) (第10题)
10. (2023东营) 如图，正方形ABCD的边长为4，点E，F分别在边DC，BC上，且BF＝CE，AE平分∠CAD，连接DF，分别交AE，AC于点G，M，P是线段AG上的一个动点，过点P作PN⊥AC，垂足为点N，连接PM，有下列四个结论：①AE垂直平分DM；②PM＋PN的最小值为3eq \r(2)；③CF2＝GE·AE；④S△ADM＝6eq \r(2).其中正确的是( )
A．①② B．②③④ C．①③④ D．①③
二、填空题(每题3分，共24分)
11．如图，已知eq \f(AD,AE)＝eq \f(AC,AB)，AD＝3 cm，AC＝6 cm，BC＝8 cm，则DE＝________.
(第11题) (第13题)
12．已知点A(－2，y1)，B(a，y2)，C(3，y3)在反比例函数y＝－eq \f(4,x)的图象上，且－213．如图所示的是一个几何体的三视图，则这个几何体的侧面积为________．
14. (2023营口二模) 某水果销售网络平台以2.6元/kg的成本价购进20 000 kg沃柑．如下表是平台销售部通过随机取样，得到的“沃柑损坏率”统计表的一部分，从而可大约估计每千克沃柑的实际售价定为________元时(精确到0.1元)，可获得13 000元利润．(销售总金额－损耗总金额－销售部分成本＝销售总利润)
15.若关于x的方程x2－3x＋m＝0有两个不相等的实数根，且m≥－3，则从满足条件的所有整数m中随机选取一个，恰好是负数的概率是________．
16．【新趋势 学科内综合】若矩形ABCD的两邻边长分别为一元二次方程x2－7x＋12＝0的两个实数根，则矩形ABCD的对角线长为________．
17. 如图，已知点A是一次函数y＝eq \f(1,3)x图象上y轴右侧的一点，过点A作x轴的垂线l，B是l上一点(点B在A上方)，在AB的右侧以AB为斜边作等腰直角三角形ABC，反比例函数y＝eq \f(k,x)(x>0)的图象过点B，C，若△OAB的面积为12，则△ABC的面积是________．
18.如图，在平面直角坐标系中，菱形ABCD的顶点A，B在x轴上，
AB＝2，A(1，0)，∠DAB＝60°，将菱形ABCD绕点A旋转90°后，得到菱形AB1C1D1，则点C1的坐标是________．
三、解答题(19～20题每题8分，21～25题每题10分，共66分)
19．解下列方程：
(1)(x＋1)2－4＝0； (2)x(x－2)＝x－2.
20. (2023鄂州) 如图，点E是矩形ABCD的边BC上的一点，且AE＝AD.
(1)尺规作图：作∠DAE的平分线AF，交BC的延长线于点F，连接DF.(保留作图痕迹，不写作法)；
(2)试判断四边形AEFD的形状，并说明理由．
21．画出如图所示的几何体的三视图．
22.（新考向 传统文化）藏毯作为青海省非物质文化遗产项目之一，与波斯毯、东方毯并称为世界三大名毯．西宁作为藏毯之都，生产的藏毯已成为青海名副其实的特色产品，更是一张通往世界的“金名片”．
(1)为了调查一批藏毯的质量，质检人员从中随机抽取了100件产品进行检测．本次抽样调查的样本容量是________；
(2)6月10日是我国文化和自然遗产日．某校举办非遗文化进校园活动，决定从A，B，C，D四名同学中随机抽取两人作为“小小宣传员”，为大家介绍青海藏毯文化．请用画树状图或列表的方法求出A，B两人同时被选中的概率．
23．【新考向 传统文化】正月十五是中华民族的传统节日——元宵节，家家挂彩灯、户户吃汤圆已成为世代相沿的习俗．某手工汤圆店计划在元宵节前用21天的时间生产袋装手工汤圆，已知每袋汤圆需要0.3斤汤圆馅和0.5斤汤圆粉，而汤圆店每天能生产450斤汤圆馅或300斤汤圆粉(每天只能生产其中一种)．
(1)若这21天生产的汤圆馅和汤圆粉恰好配套，且全部及时加工成汤圆，则总共生产了多少袋手工汤圆？
(2)为保证手工汤圆的最佳口感，汤圆店计划把这21天生产的汤圆放在近10天内销售．据统计，每袋手工汤圆的成本为13元，售价为25元时每天可售出225袋，售价每降低2元，每天可多售出75袋．汤圆店按售价25元销售2天后，余下8天进行降价促销，第10天结束后将还未售出的手工汤圆以15元/袋的价格全部卖给古城小吃店，若最终获利40 500元，则促销时每袋应降价多少元？
24．如图，一次函数y＝ax＋b的图象与x轴交于点A(4，0)，与y轴交于点B，与反比例函数y＝eq \f(k,x)(x＞0)的图象交于点C，D.若BO：OA＝2：1，BC＝3AC.
(1)求一次函数和反比例函数的表达式；
(2)求△OCD的面积．
25．【新视角 动点探究题】如图，在Rt△ABC中，∠ACB＝90°，AC＝6 cm，BC＝8 cm，动点P从点B出发，在BA边上以5 cm/s的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以4 cm/s的速度向点B匀速运动，运动时间为t s(0＜t＜2)，连接PQ.
(1)若△BPQ和△ABC相似，求t的值；
(2)连接AQ，CP，若AQ⊥CP，求t的值．
答案
一、1.B 2.B 3.D 4.C 5.C 6.C 7.A
8．C 解析：过点A作AE⊥OC于点E，
则AE∥BC，∠OEA＝∠OCB＝90°.
∴∠OAE＝∠OBC.
∴△OAE∽△OBC.
∴eq \f(S△OAE,S△OBC)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(OA,OB)))eq \s\up12(2)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(2)＝eq \f(1,4).
∵S△OAE＝eq \f(k,2)，∴S△OBC＝4S△OAE＝2k.
∴S△OBC＝S△OCD＋S△BOD＝eq \f(k,2)＋6＝2k，
解得k＝4.
9．B
10．D 解析： ∵四边形ABCD为正方形，
∴BC＝CD＝AD，∠ADE＝∠DCF＝90°.
∵BF＝CE，∴DE＝FC.
∴△ADE≌△DCF(SAS)．∴∠DAE＝∠FDC.
∵∠ADE＝90°，∴∠ADG＋∠FDC＝90°.
∴∠ADG＋∠DAE＝90°.∴∠AGD＝∠AGM＝90°.
∵AE平分∠CAD，∴∠DAG＝∠MAG.
又∵AG＝AG，∴△ADG≌△AMG(ASA)．
∴DG＝GM，∴AE垂直平分DM.
故①正确．
易知∠ADE＝∠DGE＝90°，∠DAE＝∠GDE，
∴△ADE∽△DGE，∴eq \f(DE,GE)＝eq \f(AE,DE).
∴DE2＝GE·AE.
又∵DE＝CF，
∴CF2＝GE·AE.故③正确．
∵正方形ABCD的边长为4，
∴在Rt△ABC中，AC＝eq \r(AB2＋BC2)＝eq \r(42＋42)＝4eq \r(2).
∵△ADG≌△AMG，
∴AM＝AD＝4.
由图可知△ADM中AM边上的高与△ADC中AC边上的高相等，设△ADM中边AM上的高为h，则△ADC中AC边上的高为h.
∵eq \f(1,2)×AC×h＝eq \f(1,2)×AD×DC，∴h＝eq \f(AD×DC,AC)＝2eq \r(2).
∴S△ADM＝eq \f(1,2)·AM·h＝eq \f(1,2)×4×2eq \r(2)＝4eq \r(2).
故④不正确．
∵DM⊥AG，DG＝GM，
∴点M关于线段AG的对称点为点D.
过点D作DN′⊥AC于点N′，连接PD，如图所示．
则PD＝PM.∴PM＋PN＝PD＋PN≥DN′.
∴PM＋PN的最小值即为DN′.
又∵DN′＝h＝2eq \r(2)，∴PM＋PN的最小值为2eq \r(2).故②不正确．
综上所述，正确的是①③.
二、11.4 cm 12.y315.eq \f(1,2) 16.5
17．8 解析：过点C作CD⊥y轴于点D，交AB于点E.
∵AB⊥x轴， ∴CD⊥AB.
又∵△ABC是等腰直角三角形，
∴BE＝AE＝CE.
设AB＝2a，则BE＝AE＝CE＝a.
设Aeq \b\lc\(\rc\)(\a\vs4\al\c1(x，\f(1,3)x))，则Beq \b\lc\(\rc\)(\a\vs4\al\c1(x，\f(1,3)x＋2a))，Ceq \b\lc\(\rc\)(\a\vs4\al\c1(x＋a，\f(1,3)x＋a)).
∵点B，C均在反比例函数y＝eq \f(k,x)(x>0)的图象上，
∴xeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)x＋2a))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋a))eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)x＋a))，
解得x＝eq \f(3,2)a.
∵S△OAB＝eq \f(1,2)AB·DE＝eq \f(1,2)·2a·x＝12，
∴ax＝12.∴eq \f(3,2)a2＝12.∴a2＝8.
∴S△ABC＝eq \f(1,2)AB·CE＝eq \f(1,2)·2a·a＝a2＝8.
18．(1－eq \r(3)，3)或(1＋eq \r(3)，－3) 解析：当菱形ABCD绕点A顺时针旋转90°时，如图①，延长C1D1交x轴于点E.
易得C1D1＝AD1＝AD＝AB＝2.
∵∠DAB＝60°，∠D1AD＝90°，
∴∠D1AB＝30°.
∵在菱形ABCD中，AB∥CD，∴∠ADC＝120°.
∴∠AD1C1＝∠ADC＝120°.
∴∠AD1E＝60°.∴∠AED1＝90°.
∴ED1＝eq \f(1,2)AD1＝1.
∴C1E＝2＋1＝3，AE＝eq \r(22－12)＝eq \r(3)，∴OE＝1＋eq \r(3)，
∴C1(1＋eq \r(3)，－3)．
当菱形ABCD绕点A逆时针旋转90°时，如图②，延长C1D1交x轴于点F.
同理可得OF＝eq \r(3)－1，C1F＝3.∴C1(1－eq \r(3)，3)．
综上所述，C1的坐标为(1－eq \r(3)，3)或(1＋eq \r(3)，－3)．
三、19.解：(1)移项，得(x＋1)2＝4，
两边开平方，得x＋1＝±2，
即x＋1＝2或x＋1＝－2.∴x1＝1，x2＝－3.
(2)移项，得x(x－2)－(x－2)＝0.
提取公因式，得(x－1)(x－2)＝0，
∴x－1＝0或x－2＝0，∴x1＝1，x2＝2.
20．解：(1)作图如图所示．
(2)四边形AEFD是菱形．理由如下：
∵在矩形ABCD中，AD∥BC，
∴∠DAF＝∠AFE.
∵AF平分∠DAE，∴∠DAF＝∠EAF.
∴∠AFE＝∠EAF.
∴AE＝EF.
∵AE＝AD，∴AD＝EF.
又∵AD∥EF，
∴四边形AEFD是平行四边形．
又∵AE＝AD，
∴平行四边形AEFD是菱形．
21．解：如图所示．
22．解：(1)100
(2)根据题意列表如下：
由表格可知，共有12种等可能的结果，其中A，B两人同时被选中的结果共有2种，即AB，BA，所以P(A，B两人同时被选中)＝eq \f(1,6).
23．解：(1)设总共生产了a袋手工汤圆，
依题意得eq \f(0.3a,450)＋eq \f(0.5a,300)＝21，解得a＝9 000.
答：总共生产了9 000袋手工汤圆．
(2)设促销时每袋应降价x元，
若刚好10天全部卖完，
则依题意得225×2×(25－13)＋8×(25－13－x)(225＋eq \f(75,2)x)＝40 500，
整理得x2－6x＋45＝0，
∵Δ＝(－6)2－4×45<0，∴方程无解．
∴10天不能全部卖完．
∴第10天结束后将还未售出的手工汤圆以15元/袋的价格全部卖给古城小吃店的利润为(15－13)[9 000－2×225－8×eq \b\lc\(\rc\)(\a\vs4\al\c1(225＋\f(75,2)x))]＝13 500－600x(元)．
依题意得225×2×(25－13)＋8×(25－13－x)eq \b\lc\(\rc\)(\a\vs4\al\c1(225＋\f(75,2)x))＋13 500－600x＝40 500，
整理得，x2－4x＝0，解得x1＝0，x2＝4.
∵要促销，∴x＝4.
即促销时每袋应降价4元．
24．解：(1)∵A(4，0)，∴OA＝4.
又∵BO：OA＝2：1，
∴OB＝8.∴B(0，8)．
∵A，B两点在直线y＝ax＋b上，
∴eq \b\lc\{(\a\vs4\al\c1(4a＋b＝0，,b＝8，))解得eq \b\lc\{(\a\vs4\al\c1(a＝－2，,b＝8.))
∴一次函数的表达式为y＝－2x＋8.
如图，过点C作CE⊥OA于点E.
∵BC＝3AC，∴AB＝4AC.
易知CE∥OB，
∴△ACE∽△ABO.
∴eq \f(CE,OB)＝eq \f(AE,OA)＝eq \f(AC,AB)＝eq \f(1,4).
∴CE＝2，AE＝1.∴OE＝3.
∴C(3，2)．
∵点C在反比例函数y＝eq \f(k,x)(x>0)的图象上，
∴k＝3×2＝6.∴反比例函数的表达式为y＝eq \f(6,x).
(2)由(1)建立方程组eq \b\lc\{(\a\vs4\al\c1(y＝－2x＋8，,y＝\f(6,x).))
解得eq \b\lc\{(\a\vs4\al\c1(x1＝1，,y1＝6.)) eq \b\lc\{(\a\vs4\al\c1(x2＝3，,y2＝2.))
∴D(1，6)．
如图，过点D作DF⊥y轴于点F，则DF＝1.
∴S△OCD＝S△AOB－S△BOD－S△COA＝eq \f(1,2)·OA·OB－eq \f(1,2)·OB·DF－eq \f(1,2)·OA·CE＝eq \f(1,2)×4×8－eq \f(1,2)×8×1－eq \f(1,2)×4×2＝8.
25．解：(1)由题易知AB＝10 cm，BP＝5t cm，CQ＝4t cm，
∴BQ＝(8－4t) cm.
当△PBQ∽△ABC时，有eq \f(BP,BA)＝eq \f(BQ,BC)，即eq \f(5t,10)＝eq \f(8－4t,8)，
∴t＝1.
当△QBP∽△ABC时，有eq \f(BQ,BA)＝eq \f(BP,BC)，
即eq \f(8－4t,10)＝eq \f(5t,8)，∴t＝eq \f(32,41).
∴若△BPQ和△ABC相似，则t＝1 或t＝eq \f(32,41) .
(2)如图，过点P作PD⊥BC于点D，则PD∥AC.
易得△PBD∽△ABC.∴eq \f(BP,AB)＝eq \f(PD,AC)＝eq \f(BD,BC).
由(1)知AB＝10 cm，BP＝5t cm，
可求得PD＝3t cm，BD＝4t cm，
∴CD＝(8－4t) cm.
∵AQ⊥CP，∠ACB＝90°，
∴∠CAQ＋∠ACP＝90°，∠DCP＋∠ACP＝90°.
∴∠CAQ＝∠DCP.
又∵∠CDP＝∠ACQ＝90°，∴△CPD∽△AQC.
∴eq \f(CD,AC)＝eq \f(PD,QC)，即eq \f(8－4t,6)＝eq \f(3t,4t)＝eq \f(3,4).∴t＝eq \f(7,8).
点易错：解答动态问题时，要注意分类讨论思想的应用．相似三角形对应边的位置不同，解出来的t值也不同，应充分考虑所有可能出现的情况，避免漏解．沃柑总质量n/kg
…
100
200
300
400
500
损坏沃柑质量m/kg
…
10.44
19.63
30.62
39.54
50.67
沃柑损坏的频率eq \f(m,n)(精确到0.001)
…
0.104
0.098
0.102
0.099
0.101
第一人
A
B
C
D
第二人
A
—
BA
CA
DA
B
AB
—
CB
DB
C
AC
BC
—
DC
D
AD
BD
CD
—