2023-2024学年浙江省绍兴市诸暨市七年级（下）期末数学试卷 含详解

这是一份2023-2024学年浙江省绍兴市诸暨市七年级（下）期末数学试卷 含详解，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．若分式有意义，则x的取值范围是（ ）
A．x≠5B．x＝5C．x＜5D．x＞5
2．空气中PM2.5的平均浓度为0.000037g/m3，数0.000037用科学记数法表示为（ ）
A．3.7×10﹣4B．3.7×104C．3.7×10﹣5D．3.7×105
3．下列调查中，适合采用全面调查方式的是（ ）
A．对某市居民年人均消费情况的调查
B．对某市五泄湖的水质情况的调查
C．对某电视台《民情直播》栏目喜爱程度的调查
D．对某市某班50名学生开展“创建全国卫生城市”的知晓率的调查
4．下列计算正确的是（ ）
A．（a2﹣ab）÷a＝a﹣abB．a2•a3＝a5
C．（a+b）2＝a2+b2D．3a（a2）3＝3a6
5．下列从左到右的变形为因式分解的是（ ）
A．x（x﹣1）＝x2﹣x
B．（a+4）（a﹣4）＝a2﹣16
C．2024a2﹣2024＝2024（a+1）（a﹣1）
D．x2+x﹣5＝（x﹣2）（x+3）+1
6．如果分式中的x、y都扩大为原来的2倍，那么分式的值（ ）
A．扩大为原来的2倍B．扩大为原来的4倍
C．不变D．不能确定
7．《九章算术》“盈不足”一卷中有这样一个问题：“今有善田一亩，价三百；恶田七亩，价五百．今并买一顷，价钱一万．问善、恶田各几何？”意思是：“今有好田1亩，价值300钱；坏田7亩，价值500钱．今共买好、坏田1顷（1顷＝100亩），总价值10000钱．问好、坏田各买了多少亩？设好田买了x亩，坏田买了y亩，则下面所列方程组正确的是（ ）
A．
B．
C．
D．
8．一次数学实践活动中，小鹏将一条对边互相平行的纸带沿EF折叠（如图），若AB∥CD，∠1＝65°，则∠2为（ ）
A．30°B．40°C．50°D．60°
9．已知3a÷3b＝9，ab＝3，则a+b的值为（ ）
A．16B．4C．﹣4D．±4
10．如图，直线AB∥CD，现将一副直角三角尺按如下步骤及要求摆放于同一平面内：
步骤1：将一块含30°（∠GFE＝30°）的直角三角尺（△EFG）如图放置，使得点E，F落于直线CD上，直角顶点G位于两平行线之间；
步骤2：将另一块含45°（∠MPN＝∠MNP＝45°）的直角三角尺（△PMN）进行放置，使得点P落于直线AB上（点P在点A的右边），边MN经过点G，满足∠EGN＝40°；
根据以上步骤，∠APM的度数可以是①～⑥选项中的哪三项（ ）
①10°；②20°；③70°；④80°；⑤160°；⑥170°．
A．①③⑥B．①④⑥C．②④⑤D．②③⑤
二、填空题（本大题有8小题，每小题3分，共24分）
11．已知方程3x+y＝6，用关于x的代数式表示y，则y＝ ．
12．如图，七年级某班45名男生50米跑步成绩（精确到0.1秒），组别为8.85～9.25秒的频率是 ．
七年级某班45名男生50米跑步成绩频数表
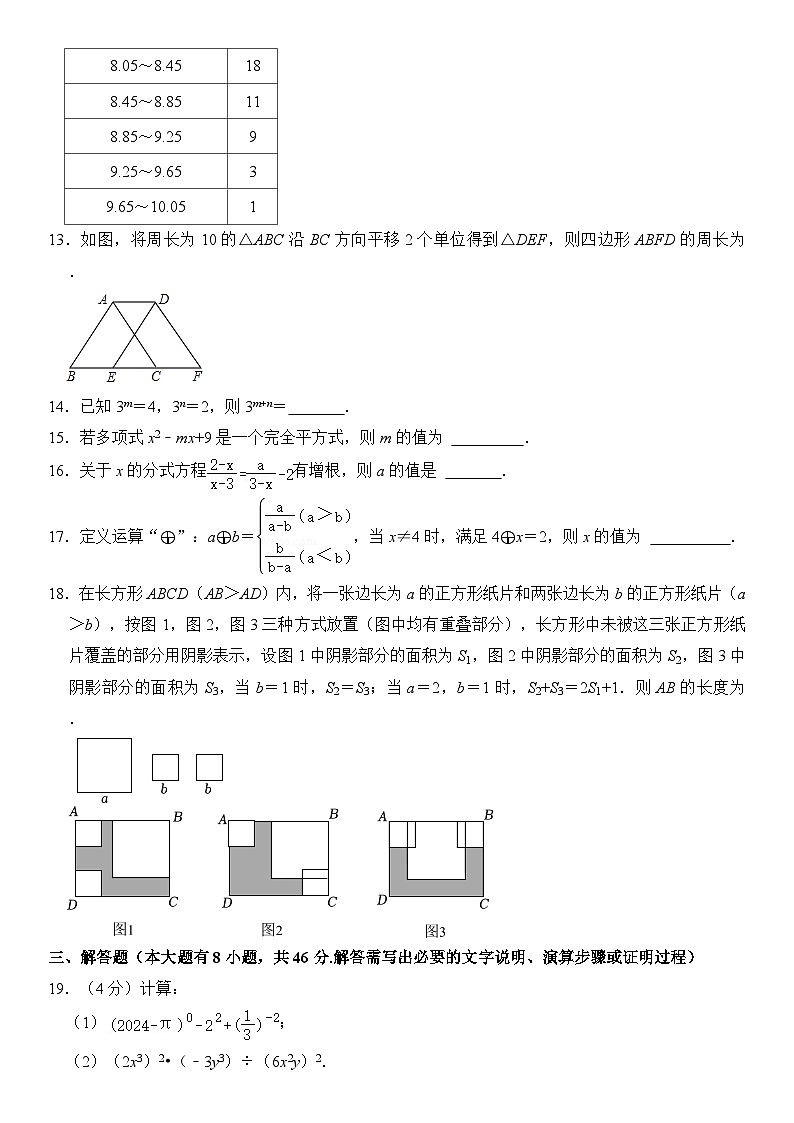
13．如图，将周长为10的△ABC沿BC方向平移2个单位得到△DEF，则四边形ABFD的周长为 ．
14．已知3m＝4，3n＝2，则3m+n＝ ．
15．若多项式x2﹣mx+9是一个完全平方式，则m的值为 ．
16．关于x的分式方程有增根，则a的值是 ．
17．定义运算“⊕”：a⊕b＝，当x≠4时，满足4⊕x＝2，则x的值为 ．
18．在长方形ABCD（AB＞AD）内，将一张边长为a的正方形纸片和两张边长为b的正方形纸片（a＞b），按图1，图2，图3三种方式放置（图中均有重叠部分），长方形中未被这三张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2，图3中阴影部分的面积为S3，当b＝1时，S2＝S3；当a＝2，b＝1时，S2+S3＝2S1+1．则AB的长度为 ．
三、解答题（本大题有8小题，共46分.解答需写出必要的文字说明、演算步骤或证明过程）
19．（4分）计算：
（1）；
（2）（2x3）2•（﹣3y3）÷（6x2y）2．
20．（4分）分解因式：
（1）3a3﹣3a；
（2）2xy2﹣8xy+8x．
21．（6分）解下列方程（组）：
（1）；
（2）．
22．（6分）先化简，再求值：，其中a＝2023，b＝2024．
23．（6分）某校开展以“青春飞扬，向阳而生”为主题的春季趣味运动会，本次趣味运动会分为甲、乙、丙三组进行．下面两幅统计图反映了学生参加趣味运动会的报名情况，请你根据图中的信息回答下列问题：
（1）该校学生报名参加趣味运动会的总人数为 人，并补全条形统计图；
（2）该校学生报名参加丙组的人数所占圆心角度数是 ；
（3）根据实际情况，需从甲组抽调部分学生到丙组，使丙组人数是甲组人数的3倍，应从甲组抽调多少名学生到丙组？
24．（6分）如图，点E、F、G分别在直线CD、AB、AD上，EF交AD于点G，已知∠A＝∠D，∠CEF+∠B＝180°．
（1）EF与BH平行吗？请说明理由；
（2）若∠DGE＝110°，求∠BHD的度数．
25．（6分）如图，将一张矩形纸片按如图所示分割成6块，其中有两块是边长为x的正方形，一块是边长为y的正方形（0＜x＜y）．
（1）观察图形，代数式2x2+3xy+y2可因式分解为 ；
（2）图中阴影部分面积之和记作S1，非阴影部分面积之和记作S2．
①用含x，y的代数式表示S1，S2；
②若，求的值．
26．（8分）根据以下信息，探索解决问题：
参考答案
一、选择题（本大题有10小题，每小题3分，共30分）
1．解：根据题意得，x﹣5≠0，
解得x≠5．
故选：A．
2．解：0.000037＝3.7×10﹣5．
故选：C．
3．解：A．对某市居民年人均消费情况的调查，适合抽样调查，不符合题意；
B．对某市五泄湖的水质情况的调查，适合抽样调查，不符合题意；
C．对某电视台《民情直播》栏目喜爱程度的调查，适合抽样调查，不符合题意；
D．对某市某班50名学生开展“创建全国卫生城市”的知晓率的调查，适合全面调查，符合题意．
故选：D．
4．解：（a2﹣ab）÷a＝a﹣b≠a﹣ab，故选项A计算错误；
a2•a3＝a5，故选项B计算正确；
（a+b）2＝a2+2ab+b2≠a2+b2，故选项C计算错误；
3a（a2）3＝3a7≠3a6，故选项D计算错误．
故选：B．
5．解：x（x﹣1）＝x2﹣x是乘法运算，则A不符合题意；
（a+4）（a﹣4）＝a2﹣16是乘法运算，则B不符合题意；
2024a2﹣2024＝2024（a+1）（a﹣1）符合因式分解的定义，则C符合题意；
x2+x﹣5＝（x﹣2）（x+3）+1中右边不是积的形式，则D不符合题意；
故选：C．
6．解：分式中的x、y都扩大为原来的2倍，则变为＝＝＝2×，
∴分式的值扩大为原来的2倍．
故选：A．
7．解：设他买了x亩好田，y亩坏田，
∵共买好、坏田1顷（1顷＝100亩）．
∴x+y＝100；
∵今有好田1亩，价值300钱；坏田7亩，价值500钱，购买100亩田共花费10000钱，
∴300x+y＝10000．
联立两方程组成方程组得：．
故选：B．
8．解：如图：
∵AB∥CD，
∴∠1＝∠EFC＝65°，
∴∠EFD＝180°﹣∠EFC＝115°，
由折叠得：∠EFD＝∠EFG＝115°，
∴∠2＝∠EFG﹣∠EFC＝115°﹣65°＝50°，
故选：C．
9．解：∵3a÷3b＝9，
∴3a﹣b＝32，
∴a﹣b＝2，
∴a2﹣2ab+b2＝4，
∵ab＝3，
∴a2+b2＝10，
∴a2+2ab+b2＝10+6＝16，
∴a+b＝±4．
故选：D．
10．解：如图，过点G作GH∥AB，
∵AB∥CD，
∴AB∥CD∥GH，
∴∠FGH＝∠EFG＝30°，∠AKG＝∠HGN，
∵∠EGN＝40°，∠EGF＝90°，
∴∠FGN＝50°，
∴∠AKG＝∠HGN＝80°，
∴∠BKM＝∠AKG＝80°．
∵∠M＝90°，
∴∠APM＝90°﹣∠PKM＝10°；
如图，过点G作GH∥AB，过点M作KM∥AB，
∵AB∥CD，
∴AB∥CD∥GH∥KM，
∴∠FGH＝∠EFG＝30°，∠KMG＝∠HGM，∠APM＝∠PMK，
∵∠EGN＝40°，∠EGF＝90°，
∴∠KMG＝∠HGM＝180°﹣90°﹣40°﹣30°＝20°，
∵∠PMN＝90°，
∴∠APM＝∠PMK＝90°﹣20°＝70°；
如图，过点G作KG∥AB交PN于点K，
∵AB∥CD，
∴AB∥CD∥GK，
∴∠FGK＝∠EFG＝30°，∠APK＝∠PKG，
∵∠EGN＝40°，∠EGF＝90°，
∴∠FGN＝50°，∠KGN＝80°，
∴∠NKG＝180°﹣∠PNM﹣∠KGN＝55°，
∴∠APK＝∠PKG＝180°﹣∠GKN＝125°，
∠APM＝∠APN+∠MPN＝170°．
故选：A．
二、填空题（本大题有8小题，每小题3分，共24分）
11．解：3x+y＝6，
移项，得y＝6﹣3x，
故答案为：6﹣3x．
12．解：组别为8.85～9.25秒的频率是＝0.2．
故答案为：0.2．
13．解：∵△ABC沿BC方向平移2个单位得到△DEF，
∴AD＝CF＝2，
∴四边形ABFD的周长，
＝AB+BC+DF+CF+AD，
＝△ABC的周长+AD+CF，
＝10+2+2，
＝14．
故答案为：14．
14．解：∵3m＝4，3n＝2，
∴3m+n＝3m×3n＝4×2＝8，
故答案为：8．
15．解：∵x2+mx+9＝x2+mx+（±3）2，
∴m＝±6，
故答案为：±6．
16．解：方程两边乘（x﹣3）得：2﹣x＝﹣a﹣2（x﹣3），
∴x＝4﹣a，
∵方程有增根，
∴x﹣3＝0，
∴4﹣a＝3，
∴a＝1．
故答案为：1．
17．解：当x＞4时，＝2，
解得x＝8，
经检验x＝8是原方程的解，
当x＜4时，＝2，
解得x＝2，
经检验x＝2是原方程的解，
综上所述x的值为2或8．
故答案为：2或8．
18．解：由图可得：
S1＝AD•AB﹣a2﹣2b2，
S2＝AD•AB﹣a2﹣b2﹣b（AD﹣a），
S3＝AD•AB﹣a2﹣b（AB﹣a），
∵当b＝1时，S2＝S3，
∴AD•AB﹣a2﹣b2﹣b（AD﹣a）＝AD•AB﹣a2﹣b（AB﹣a），
∴﹣b2﹣b（AD﹣a）＝﹣b（AB﹣a），
∴﹣1﹣（AD﹣a）＝﹣AB+a，
∴AB﹣AD＝1，
∵当a＝2，b＝1时，S2+S3＝2S1+1，
∴AD•AB﹣a2﹣b2﹣b（AD﹣a）+AD•AB﹣a2﹣b（AB﹣a）＝2（AD•AB﹣a2﹣2b2）+1，
∴2AD•AB﹣2a2﹣b2﹣b（ AD﹣a）﹣b（AB﹣a）＝2AD•AB﹣4b2﹣2a2+1，
∴3b2﹣b（AD﹣a）﹣b（AB﹣a）＝1，
∴3×1﹣（AD﹣2）﹣（AB﹣2）＝1，
∴AB+AD＝6，
又∵AB﹣AD＝1，
∴AB+AB﹣1＝6，
∴AB＝3.5．
故答案为：3.5．
三、解答题（本大题有8小题，共46分.解答需写出必要的文字说明、演算步骤或证明过程）
19．解：（1）
＝1﹣4+9
＝6；
（2）（2x3）2•（﹣3y3）÷（6x2y）2
＝4x6•（﹣3y3）÷36x4y2
＝﹣12x6y3）÷36x4y2
＝﹣x2y．
20．解：（1）3a3﹣3a
＝3a（a2﹣1）
＝3a（a+1）（a﹣1）；
（2）2xy2﹣8xy+8x
＝2x（y2﹣4y+4）
＝2x（y﹣2）2．
21．解：（1），
①+②×2得：5x＝10，
解得：x＝2，
将x＝2代入②得：2﹣y＝3，
解得：y＝﹣1，
故原方程组的解为；
（2）原方程去分母得：x+1＝﹣x+x﹣2，
解得：x＝﹣3，
检验：当x＝﹣3时，x﹣2≠0，
故原方程的解为x＝﹣3．
22．解：
＝•
＝•
＝b﹣a，
当a＝2023，b＝2024时，原式＝2024﹣2023＝1．
23．解：（1）该校学生报名参加趣味运动会的总人数为：15÷30%＝50（人），
乙组人数为：50×20%＝10（人），
补全条形统计图如图所示：
故答案为：50；
（2）该校学生报名参加丙组的人数所占圆心角度数是：360°×（1﹣20%﹣30%）＝180°，
故答案为：180°；
（3）设应从甲组抽调x名学生到丙组，
由题意得，25+x＝3（15﹣x），
解得，x＝5，
答：应从甲组抽调5名学生到丙组．
24．解：（1）EF∥BH，理由如下：
∵∠A＝∠D，
∴AB∥CD，
∴∠CEF+∠AFE＝180°，
∵∠CEF+∠B＝180°，
∴∠AFE＝∠B，
∴EF∥BH；
（2）∵∠DGE＝110°，
∴∠DGF＝180°﹣110°＝70°，
∵EF∥BH，
∴∠BHD＝∠DGF＝70°．
25．解：（1）观察图形可知，2x2+y2 表示空白部分的面积，3xy表示阴影部分的面积，
∴2x2+3xy+y2表示矩形纸片的面积，而矩形纸片的长为2x+y，宽为x+y，
∴2x2+3xy+y2 可因式分解为（2x+y）（x+y）．
故答案为：（2x+y）（x+y）；
（2）①观察图形可得：S1＝xy+xy+xy＝3xy，；
②∵，
∴3xy﹣2x2﹣y2＝2x2﹣xy，
整理，得4x2﹣4xy+y2＝0，
∴（2x﹣y）2＝0，
∴2x﹣y＝0，
∴y＝2x，
∴
＝
＝
＝1．
26．解：问题1：∵每天满工作量情况下，乙工厂每天加工数量是甲工厂每天加工数量的1.5倍，且甲工厂每天加工数量为x件，
∴乙工厂每天加工数量为1.5x件．
故答案为：1.5x；
问题2：根据题意得：﹣＝10，
解得：x＝50，
经检验，x＝50是所列方程的解，其符合题意．
答：每天满工作量情况下，甲工厂每天能加工50件新产品；
问题3：设每天满工作量情况下，甲工厂加工1天所需费用为m元，乙工厂加工1天所需费用为n元，
根据题意得：，
解得：，
∴每天满工作量情况下，甲工厂加工新产品的单价为2200÷50＝44（元/件），
乙工厂加工新产品的单价为3900÷（1.5×50）＝52（元/件）．
设交给甲工厂y件新产品进行加工，则交给乙工厂（1500﹣y）件新产品进行加工，
根据题意得：＝n（44＜n＜52，且n为整数），
∴y＝（52﹣n）．
∵y为正整数，
∴n可以为46，48，50，
当n＝46时，y＝×（52﹣46）＝1125，
此时+＝（天），符合题意；
当n＝48时，y＝×（52﹣48）＝750，
此时+＝25（天），不符合题意，舍去；
当n＝50时，y＝×（52﹣50）＝375，
此时+＝（天），符合题意．
答：交给甲工厂1125或375件新产品进行加工．
组别
频数
7.65～8.05
3
8.05～8.45
18
8.45～8.85
11
8.85～9.25
9
9.25～9.65
3
9.65～10.05
1
背景：为了提高产品的附加值，某公司计划将研发生产的1500件新产品进行加工后再投放市场．每天满工作量情况下，甲、乙两个工厂加工数量及每件加工费用保持稳定不变，公司派出相关人员分别到这两间工厂了解情况，获得如下信息．
信息1
每天满工作量情况下，乙工厂每天加工数量是甲工厂每天加工数量的1.5倍；
信息2
每天满工作量情况下，甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息3
每天满工作量情况下，甲工厂加工1天，乙工厂加工2天共需要10000元；甲工厂加工2天，乙工厂加工3天共需要16100元．
问题解决
问题1
1设每天满工作量情况下，甲工厂每天加工数量为x件，结合信息1可得：乙工厂每天加工数量为
件（请用x的代数式表示）．
问题2
每天满工作量情况下，求甲工厂每天能加工多少件新产品？
问题3
公司将1500件新产品交给甲、乙两工厂一起加工，发现这批新产品的平均加工费用为整数，两工厂加工的时间之和不是整数．请问交给甲工厂多少件新产品进行加工？