2023-2024学年山东省菏泽市巨野县八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年山东省菏泽市巨野县八年级（下）期末数学试卷（含答案），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

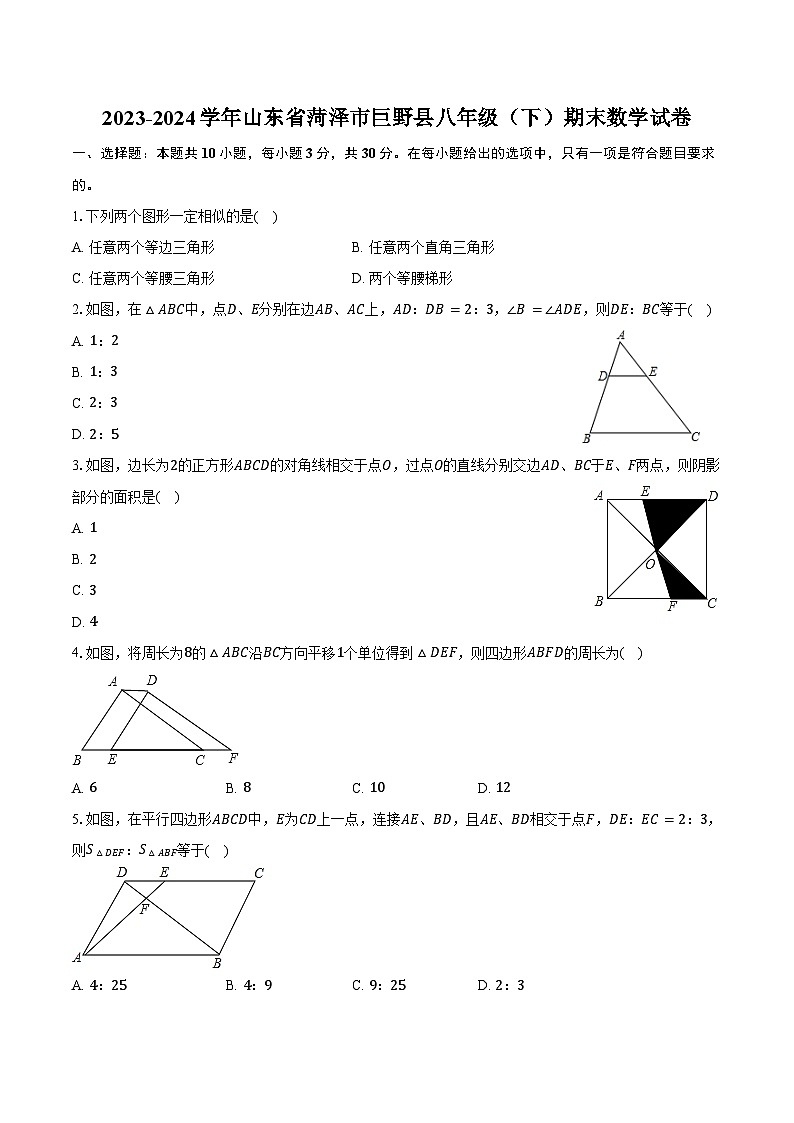
1.下列两个图形一定相似的是( )
A. 任意两个等边三角形B. 任意两个直角三角形
C. 任意两个等腰三角形D. 两个等腰梯形
2.如图，在△ABC中，点D、E分别在边AB、AC上，AD：DB=2：3，∠B=∠ADE，则DE：BC等于( )
A. 1：2
B. 1：3
C. 2：3
D. 2：5
3.如图，边长为2的正方形ABCD的对角线相交于点O，过点O的直线分别交边AD、BC于E、F两点，则阴影部分的面积是( )
A. 1
B. 2
C. 3
D. 4
4.如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为( )
A. 6B. 8C. 10D. 12
5.如图，在平行四边形ABCD中，E为CD上一点，连接AE、BD，且AE、BD相交于点F，DE：EC=2：3，则S△DEF：S△ABF等于( )
A. 4：25B. 4：9C. 9：25D. 2：3
6.已知点P(a,b)在一次函数y=−x+2的图象上，且在一次函数y=x图象的下方，则符合条件的a−b值可能是( )
A. −2B. −1C. 0D. 1
7.图1是某娱乐节目中一个游戏环节的录制现场，场地由等边△ADE和正方形ABCD组成，正方形ABCD两条对角线交于点O，在AD的中点P处放置了一台主摄像机．游戏参与者行进的时间为x，与主摄像机的距离为y，若游戏参与者匀速行进，且表示y与x的函数关系式大致如图2所示，则游戏参与者的行进路线可能是( )
A. A→O→DB. E→A→CC. A→E→DD. E→A→B
8.将正比例函数y=kx向右平移2个单位，再向下平移4个单位，平移后依然是正比例函数，则k的值为( )
A. −4B. −2C. 2D. 4
9.如图，已知一次函数y=kx+b的图象与x轴，y轴分别交于点(2,0)，点(0,3).有下列结论：①关于x的方程kx+b=0的解为x=2；②关于x的方程kx+b=3的解为x=0；③当x>2时，y<0；④当x<0时，y<3.其中正确的是( )
A. ①②③
B. ①③④
C. ②③④
D. ①②④
10.如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=2，将△ABC绕顶点C逆时针旋转得到△A′B′C′，若点M、P分别是BC、A′B′的中点，连接PM.则线段PM的最大值是( )
A. 4
B. 3
C. 2
D. 1
二、填空题：本题共6小题，每小题3分，共18分。
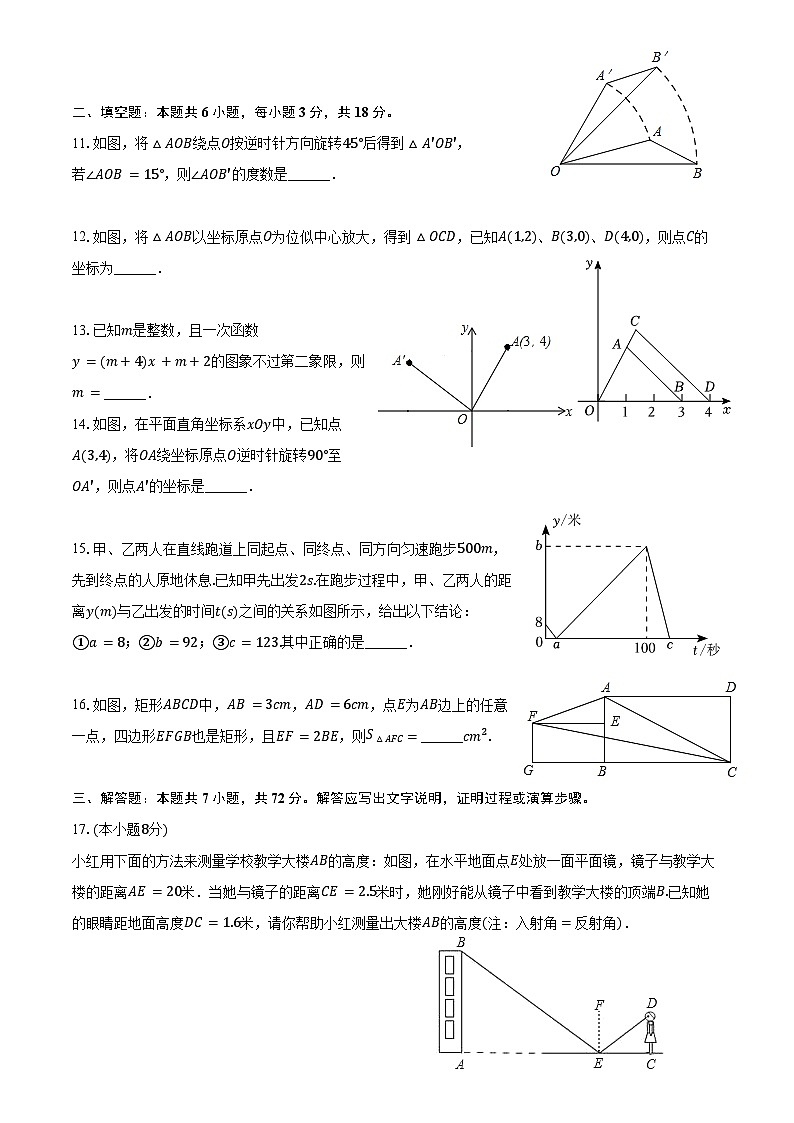
11.如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，
若∠AOB=15°，则∠AOB′的度数是______．
12.如图，将△AOB以坐标原点O为位似中心放大，得到△OCD，已知A(1,2)、B(3,0)、D(4,0)，则点C的坐标为______．
13.已知m是整数，且一次函数y=(m+4)x+m+2的图象不过第二象限，则m=______．
14.如图，在平面直角坐标系xOy中，已知点A(3,4)，将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是______．
15.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m，先到终点的人原地休息.已知甲先出发2s.在跑步过程中，甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123.其中正确的是______．
16.如图，矩形ABCD中，AB=3cm，AD=6cm，点E为AB边上的任意一点，四边形EFGB也是矩形，且EF=2BE，则S△AFC=______cm2．
三、解答题：本题共7小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
小红用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面点E处放一面平面镜，镜子与教学大楼的距离AE=20米．当她与镜子的距离CE=2.5米时，她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米，请你帮助小红测量出大楼AB的高度(注：入射角=反射角)．
18.(本小题8分)
如图，△ABC中，AB=BC，点O是△ABC内一点，将△ABO旋转后能与△BCD重合
(1)旋转中心是点______；
(2)若∠ACB=70°，旋转角是______度；
(3)若∠ACB=60°，请判断△BOD的形状并说明理由．
19.(本小题12分)
图形变换大观园：请阅读各小题的要求，利用你所学的平移与旋转知识作答．
(1)如图1，是某产品的标志图案，要在所给的图形图2中，把A，B，C三个菱形通过一种或几种变换，均可以变为与图1一样的图案.你所用的变换方法是______．

①将菱形B向上平移半径的长度；②将菱形B绕点O旋转120°；③将菱形B绕点O旋转180°．
(在以上的变换方法中，选择一种正确的填到横线上.)．
(2)分析图①、②、④中阴影部分的分布规律，并按此规律在图③中画出其中的阴影部分．

(3)如图，在平面直角坐标系中，已知点A(0,2)、B(2,2)、C(1,1)．
①若将△ABC先向左平移3个单位长度，再向下平移1个单位长度，得到△A1B1C1，请画出△A1B1C1，并写出点C1的坐标为______；
②若将△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2，直接写出点C2的坐标为______；
③若将△ABC绕点P按顺时针方向旋转90°后得到△A3B3C3，则点P的坐标是______．
20.(本小题12分)
已知函数y=(2m−2)x+m+1，
(1)m为何值时，图象过原点．
(2)已知y随x增大而增大，求m的取值范围．
(3)函数图象与y轴交点在x轴上方，求m取值范围．
(4)图象过一、二、四象限，求m的取值范围．
21.(本小题10分)
如图，直线y=−2x与直线y=kx+b 相交于点A(a,2)，并且直线y=kx+b经过x轴上点B(2,0)
(1)求直线y=kx+b的解析式．
(2)求两条直线与y轴围成的三角形面积．
(3)直接写出不等式(k+2)x+b≥0的解集．
22.(本小题10分)
某水果店5月份购进甲、乙两种水果共花费1700元，其中甲种水果8元/千克，乙种水果18元/千克．6月份，这两种水果的进价上调为：甲种水果10元/千克，乙种水果20元/千克．
(1)若该店6月份购进这两种水果的数量与5月份都相同，将多支付货款300元，求该店5月份购进甲、乙两种水果分别是多少千克？
(2)若6月份将这两种水果进货总量减少到120千克，且甲种水果不超过乙种水果的3倍，则6月份该店需要支付这两种水果的货款最少应是多少元？
23.(本小题12分)
如图，在Rt△ABC中，∠C=90°，AC=8cm，BC=6cm.现在有动点P从点B出发，沿线段BA向终点A运动，动点Q从点A出发，沿折线AC—CB向终点运动.如果点P的速度是1cm/s，点Q的速度是1cm/s.它们同时出发，当有一点到达终点时，另一点也停止运动.设运动的时间为t秒．
(1)如图1，Q在AC上，当t为多少秒时，以点A、P、Q为顶点的三角形与△ABC相似？
(2)如图2，Q在CB上，是否存着某时刻，使得以点B、P、Q为顶点的三角形与△ABC相似？若存在，求出t的值；若不存在，请说明理由．
参考答案
1.A
2.D
3.A
4.C
5.A
6.D
7.A
8.B
9.A
10.B
11.30°
12.(43,83)
13.−3或−2
14.(−4,3)
15.①②③
16.9
17.解：∵根据反射定律知：∠FEB=∠FED，
∴∠BEA=∠DEC
∵∠BAE=∠DCE=90°
∴△BAE∽△DCE
∴ABDC=AEEC；
∵CE=2.5米，DC=1.6米，
∴AB1.6=202.5；
∴AB=12.8
∴大楼AB的高为12.8米．
18.(1)B；
(2)40；
(3)△BOD是等边三角形，理由如下：
∵AB=BC，∠ACB=60°，
∴△ABC是等边三角形，
∴∠ABC=60°，
∵将△ABO旋转后能与△BCD重合，
∴BD=BO，
∵∠OBD=∠ABC=60°，
∴△BOD是等边三角形．
19.(1)③；
(2)如图③所示．
(3)①如图所示：C1的坐标为(−2,0)，
②(−1,−1)；
③(2,0)．
20.解：(1)∵函数图象过原点，
∴m+1=0，即m=−1；
(2)∵y随x增大而增大，
∴2m−2>0，解得m>1；
(3)∵函数图象与y轴交点在x轴上方，
∴m+1>0，即m>−1；
(4)∵图象过一、二、四象限，
∴2m−2<0m+1>0，解得−121.解：(1)把A(a,2)代入y=−2x中，得−2a=2，
∴a=−1，
∴A(−1,2)
把A(−1,2)，B(2,0)代入y=kx+b，
得−k+b=22k+b=0，
∴k=−23，b=43，
∴一次函数的解析式是y=−23x+43；
(2)设直线AB与y轴交于点C，则C(0,43)
∴S△AOC=12×43×1=23；
(3)不等式(k+2)x+b≥0可以变形为kx+b≥−2x，
结合图象得到解集为：x≥−1．
22.解：(1)设该店5月份购进甲种水果x千克，购进乙种水果y千克，
根据题意得：8x+18y=170010x+20y=1700+300，
解得：x=100y=50．
答：该店5月份购进甲种水果100千克，购进乙种水果50千克．
(2)设购进甲种水果a千克，需要支付的货款为w元，则购进乙种水果(120−a)千克，
根据题意得：w=10a+20(120−a)=−10a+2400．
∵甲种水果不超过乙种水果的3倍，
∴a≤3(120−a)，
解得：a≤90．
∴当a=90时，w取最小值，最小值为−10×90+2400=1500(元)．
∴6月份该店需要支付这两种水果的货款最少应是1500元．
23.解：(1)如图1，当∠AQP=90°时，△AQP∽△ACB，

∴AQAC=APAB．
在Rt△ABC中，由勾股定理，得
AB= AC2+BC2= 82+62=10(cm)．
∵BP=t，AQ=t，
∴PA=10−t，
∴t8=10−t10，
∴t=409，
如图2，当∠APQ=90°时，△APQ∽△ACB，

∴AQAB=APAC，
∴t10=10−t8，
t=509．
综上所述，t=409或509时，以点A、P、Q为顶点的三角形与△ABC相似；
(2)如图3，当△BPQ∽△BAC时，

BPAB=BQBC．
∵BQ=14−t，BP=t，
∴t10=14−t6，
∴t=354，
当△BQP∽△BAC时，
∴BQBA=BPBC，
∴t=214(舍去)，
∴t=354时，Q在CB上，以点B、P、Q为顶点的三角形与△ABC相似．