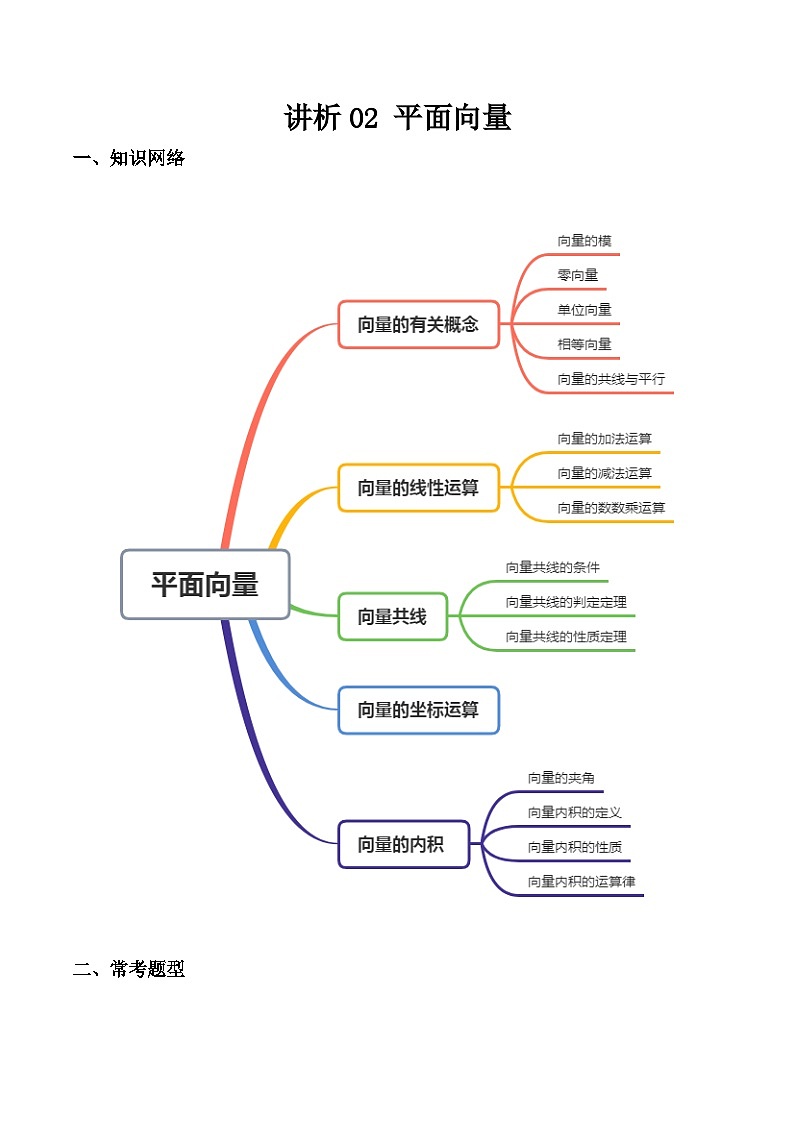

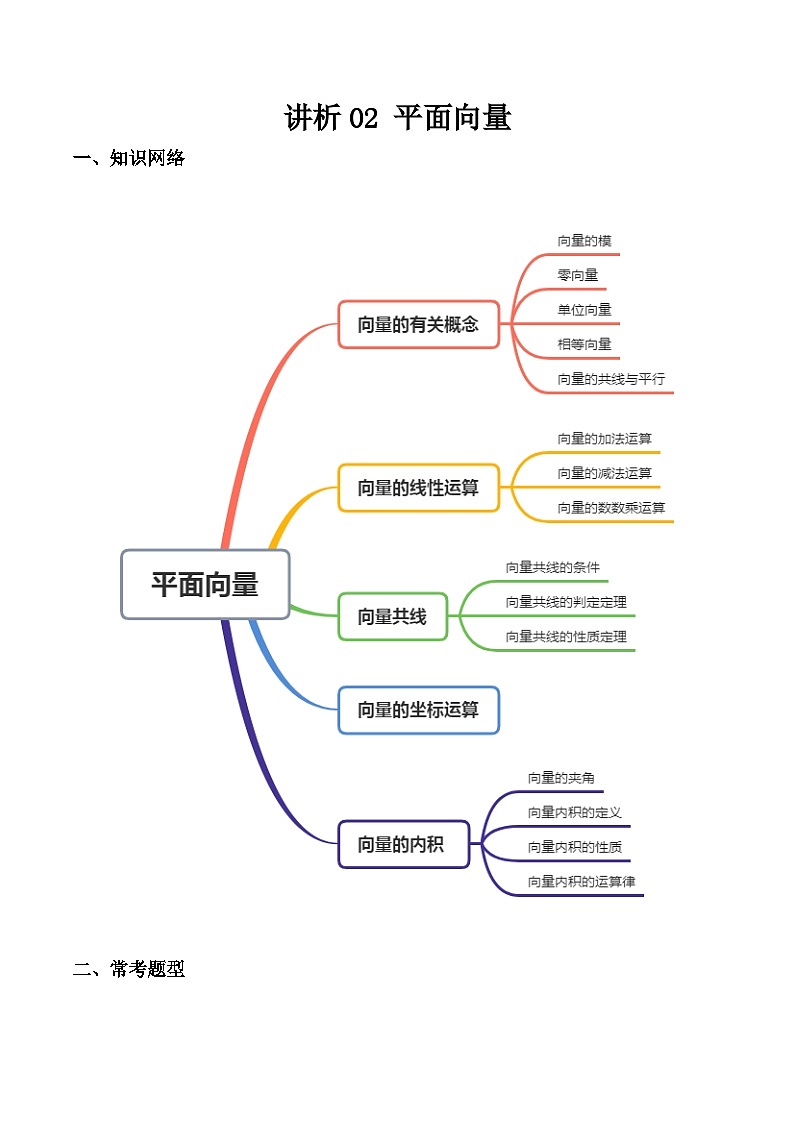

高教版(2021·十四五)第2章 平面向量优秀巩固练习
展开二、常考题型
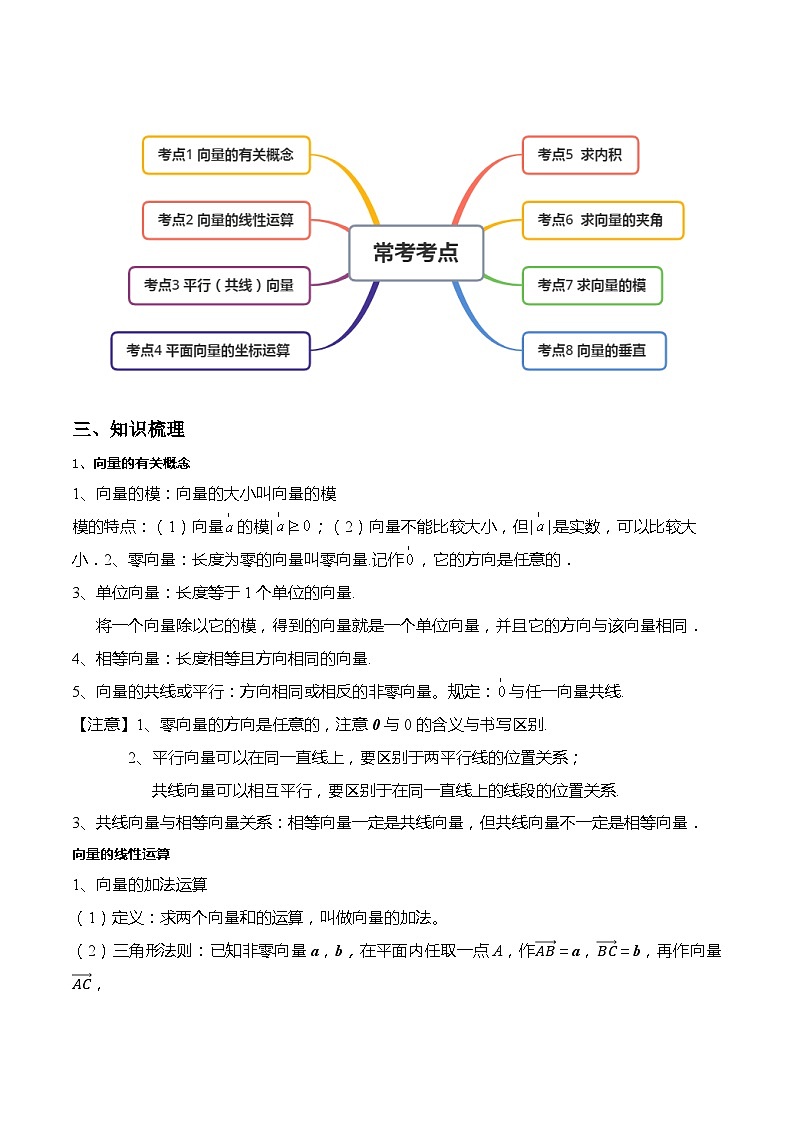
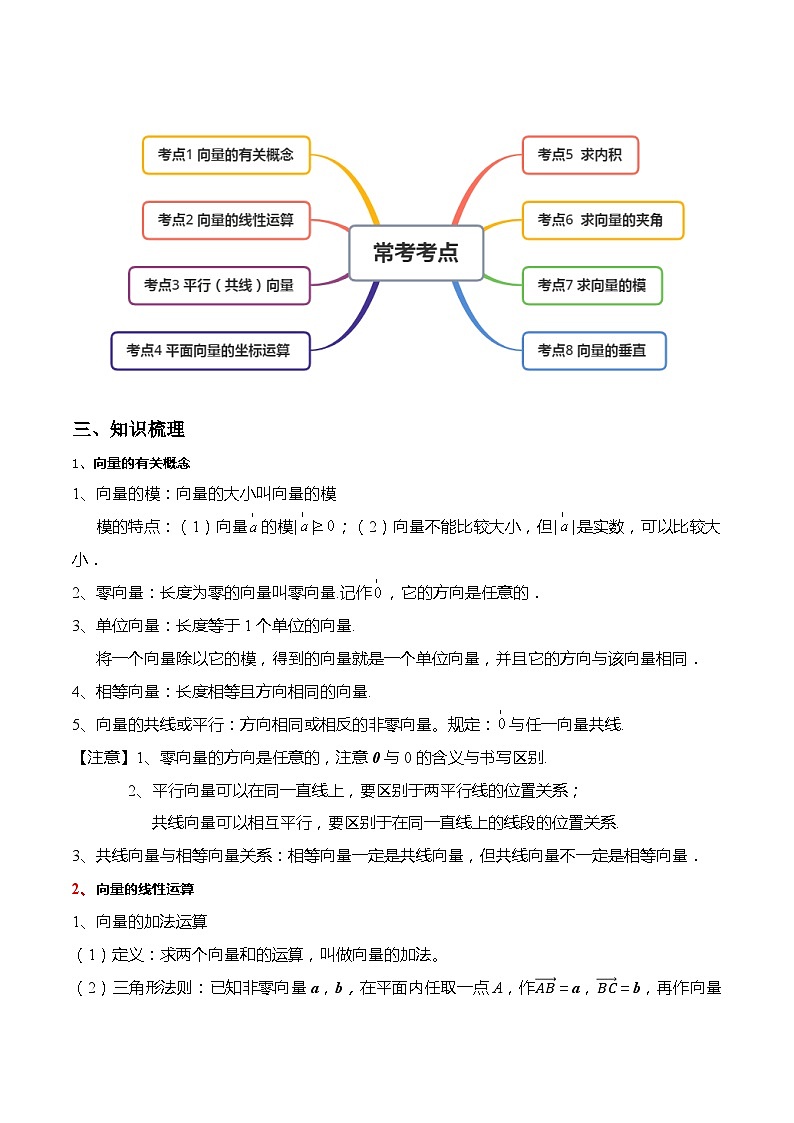
三、知识梳理
1、向量的有关概念
1、向量的模:向量的大小叫向量的模
模的特点:(1)向量的模;(2)向量不能比较大小,但是实数,可以比较大小.2、零向量:长度为零的向量叫零向量.记作,它的方向是任意的.
3、单位向量:长度等于1个单位的向量.
将一个向量除以它的模,得到的向量就是一个单位向量,并且它的方向与该向量相同.
4、相等向量:长度相等且方向相同的向量.
5、向量的共线或平行:方向相同或相反的非零向量。规定:与任一向量共线.
【注意】1、零向量的方向是任意的,注意0与0的含义与书写区别.
2、平行向量可以在同一直线上,要区别于两平行线的位置关系;
共线向量可以相互平行,要区别于在同一直线上的线段的位置关系.
3、共线向量与相等向量关系:相等向量一定是共线向量,但共线向量不一定是相等向量.
向量的线性运算
1、向量的加法运算
(1)定义:求两个向量和的运算,叫做向量的加法。
(2)三角形法则:已知非零向量a,b,在平面内任取一点A,作AB=a,BC=b,再作向量AC,
向量AC叫做a与b的和,记作a+b,即a+b=AB+BC=AC
(3)平行四边形法则:已知不共线的两个向量a,b,在平面内任取一点O,
以同一点O为起点的两个已知向量a,b为邻边作▱OACB,对角线OC就是a与b的和
【规定】零向量与任一向量a的和都有a+0eq \a\vs4\al(=)0+a=eq \a\vs4\al(a).
【注意】 = 1 \* GB3 ①在使用向量加法的三角形法则时,要注意“首尾相接”,即第一个向量的终点与第二个向量的起点重合,则以第一个向量的起点为起点,并以第二个向量的终点为终点的向量即两向量的和; = 2 \* GB3 ②平行四边形法则的应用前提是“共起点”,即两个向量是从同一点出发的不共线向量.
(4)向量加法的运算律
结合律:a+b=b+a 交换律:(a+b)+c=a+(b+c)
2、向量的减法运算
(1)相反向量:与a长度相等、方向相反的向量,叫做a的相反向量,记作-a.
= 1 \* GB3 ①规定:零向量的相反向量仍是仍是零向量;
= 2 \* GB3 ②(-a)=a;
= 3 \* GB3 ③a+(-a)=(-a)+a=0;
= 4 \* GB3 ④若a与b互为相反向量,则a=-b,b=-a,a+b=0.
【注意】相反向量与相等向量一样,从“长度”和“方向”两方面定义,相反向量必为平行向量.
(2)向量的减法
= 1 \* GB3 ①定义:a-b=a+(-b),即减去一个向量相当于加上这个向量的相反向量.
= 2 \* GB3 ②几何意义:以O为起点,作向量eq \(OA,\s\up7(―→))=a,eq \(OB,\s\up7(―→))=b,则eq \(BA,\s\up7(―→)) =a-b,
如图所示,即a-b可表示从向量b的终点指向向量a的终点的向量.
【注意】在用三角形法则作向量减法时,只要记住“连接向量终点,箭头指向被减向量”即可.
3、向量的数乘运算
(1)定义:规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作:λa,
它的长度与方向规定如下:①|λa|=|λ||a|;②当λ>0时,λa的方向与a的方向相同;
当λ<0时,λa的方向与a的方向相反.
(2)运算律:设λ,μ为任意实数,则有:
①λ(μ a)=(λμ)a; ②(λ+μ)a=λa+μ a; ③λ(a+b)=λa+λb;
特别地,有(-λ)a=λ(-a)=-(λa); λ(a-b)=λa-λb.
(3)线性运算:向量的加、减、数乘运算统称为向量的线性运算,向量线性运算的结果仍是向量.
对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a+μ2b)=λμ1a±λμ2b.
3、向量共线
1、向量共线的条件
(1)当向量时,与任一向量共线.
(2)当向量时,对于向量.如果有一个实数,使,那么由实数与向量的积的定义知与共线.
反之,已知向量与()共线且向量的长度是向量的长度的倍,即,那么当与同向时,;当与反向时,.
2、向量共线的判定定理:是一个非零向量,若存在一个实数,使,则向量与非零向量共线.
3、向量共线的性质定理:若向量与非零向量共线,则存在一个实数,使.
【注意】
(1)两个向量定理中向量均为非零向量,即两定理均不包括与共线的情况;
(2)是必要条件,否则,时,虽然与共线但不存在使;
(3)有且只有一个实数,使.
(4)是判定两个向量共线的重要依据,其本质是位置关系与数量关系的相互转化,体现了数形结合的高度统一.
4、向量的内积
1、向量的夹角
(1)定义:已知两个非零向量,,是平面上的任意一点,作,,
则()叫做向量与的夹角.
(2)性质:当时,与同向;当时,与反向.
(3)向量垂直:如果与的夹角是,我们说与垂直,记作.
2、向量的内积的定义
(1)定义:非零向量与,它们的夹角为,数量叫做向量与的内积;
(2)记法:向量与的内积记作,即;
零向量与任一向量的内积为0;
4、平面向量内积的性质
设,都是非零向量,是单位向量,θ为与(或)的夹角.则
(1);
(2);
(3)当与同向时,;当与反向时,;
特别地,或;
(4)cs θ=;
(5)
5、平面向量内积的运算律
(1);
(2)(λ为实数);
(3);
四、常考题型探究
考点一 向量的有关概念
例1.给出下列命题:
(1)平行向量的方向一定相同;
(2)向量的模一定是正数;
(3)始点不同,但方向相同且模相等的向量是相等向量;
(4)若向量eq \(AB,\s\up6(→))与eq \(CD,\s\up6(→))是共线向量,则A、B、C、D四点必在同一直线上.
其中正确的序号是__ __.
例2.如图,在正方形ABCD中,AC与BD交于点O,则图中与eq \(OA,\s\up6(→))相等的向量是( )
A.eq \(OC,\s\up6(→))B.eq \(OD,\s\up6(→))
C.eq \(OB,\s\up6(→))D.eq \(CO,\s\up6(→))
【变式探究】1. 下列命题中正确的个数是( )
①若向量与是共线向量,则A、B、C、D必在同一直线上;
②若向量与向量平行,则,方向相同或相反;
③若非零向量与是共线向量,则它们的夹角是0°或180°;
④若,则,是相等向量或相反向量.
A.0B.1C.2D.3
考点二 向量的线性运算
例3.化简下列各式:
(1)eq \(AB,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→))+eq \(FA,\s\up6(→));
(2)(eq \(AB,\s\up6(→))+eq \(DE,\s\up6(→)))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→))+eq \(EA,\s\up6(→)).
例4.如图,正六边ABCDEF中,eq \(BA,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(FE,\s\up6(→))=( )
A.0 B.eq \(BE,\s\up6(→))
C.eq \(AD,\s\up6(→)) D.eq \(CF,\s\up6(→))
例5.(1)4(a+b)-3(a-b)-8a;
(2)(5a-4b+c)-2(3a-2b+c);
(3)eq \f(2,3)[(4a-3b)+eq \f(1,3)b-eq \f(1,4)(6a-7b)].
【变式探究】1. 化简(eq \(AB,\s\up6(→))-eq \(CD,\s\up6(→)))-(eq \(AC,\s\up6(→))-eq \(BD,\s\up6(→))).
2. 如图,正六边ABCDEF中,eq \(BA,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(FE,\s\up6(→))=( B )
A.0B.eq \(BE,\s\up6(→))
C.eq \(AD,\s\up6(→))D.eq \(CF,\s\up6(→))
3.计算:
(1)eq \f(2,5)(a-b)-eq \f(1,3)(2a+4b)+eq \f(2,15)(2a+13b);
(2)(m+n)(a-b)-(m-n)(a+b).
考点三 平行(共线)向量
例6. 已知是平面内不共线的两个向量,且,,若,则实数( )
A.B.C.6D.
例7. 已知向量eq \(AB,\s\up6(→))=a+5b,eq \(BC,\s\up6(→))=-2a+8b,eq \(CD,\s\up6(→))=3(a-b),
求证:A、B、D三点共线;
【变式探究】设两个非零向量a与b不共线,
(1)若eq \(AB,\s\up6(→))=a+b,eq \(BC,\s\up6(→))=2a+8b,eq \(CD,\s\up6(→))=3(a-b),求证:A、B、D三点共线;
(2)试确定实数k,使ka+b与a+kb共线.
考点四平面向量的坐标运算
例8. 已知向量,则__________.
例9. 已知向量,若,则( )
A.-1 B.2 C.-6 D.6
【变式探究】1、已知向量,若满足,则等于( )
A. B. C. D.
2、已知向量,,,若与共线,则( )
A.4 B.3 C.2 D.1
考点五 求内积
例10.已知|a|=2,|b|=3,a与b的夹角为120°,试求:
①a·b;
②(a+b)·(a-b);
③(2a-b)·(a+3b).
例11.已知向量,若,则( )
A.B.3C.D.1
【变式探究】1. 已知,,则( )
A.-3B.-2C.2D.3
考点六 求向量的夹角
例12. 已知,,,则与的夹角是( )
A.B.C.D.
例13.已知向量,则向量的夹角的余弦值为 .
【变式探究】1、已知,,则,夹角的大小为 .
2、已知向量,则向量与夹角的余弦值为( )
A.B.C.D.1
考点七 求向量的模
例14. 已知向量,,则( )
A.2B.3C.4D.5
例15.已知,,且,则( )
A.1B.C.D.5
【变式探究】1、已知向量,则等于( )
A.2B.3
C.3D.5
2、已知向量a,b的夹角为120°,|a|=4,|b|=3,则|a-3b|=__eq \r(133)__.
考点八 向量的垂直
例16.已知,且, 则的值为( )
A.B.3C.D.9
例17. 已知非零单位向量的夹角为,若与垂直,则实数的值为( )
A.B.C.D.
【变式探究】1. 已知量,,若,则( )
A.B.C.D.2
2、设,向量,,且,则( )
A. B. C. D.5
高教版(2021)拓展模块一 上册2.1 向量的概念优秀同步训练题: 这是一份高教版(2021)拓展模块一 上册<a href="/sx/tb_c4035768_t7/?tag_id=28" target="_blank">2.1 向量的概念优秀同步训练题</a>,文件包含第2章平面向量过关测试-中职专用高中数学单元复习讲与测高教版2021·拓展模块一上册原卷版docx、第2章平面向量过关测试-中职专用高中数学单元复习讲与测高教版2021·拓展模块一上册解析版docx等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
中职数学高教版(中职)基础模块上册复习题3精品单元测试习题: 这是一份中职数学高教版(中职)基础模块上册复习题3精品单元测试习题,共12页。试卷主要包含了单选题等内容,欢迎下载使用。
高教版(中职)基础模块上册复习题3精品单元测试综合训练题: 这是一份高教版(中职)基础模块上册复习题3精品单元测试综合训练题,共11页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。












